Задачей КП называется следующая задача:
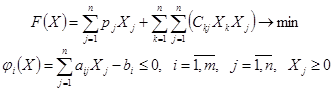
В матричном виде: пусть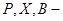 
векторы-столбцы:
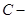матрица квадратичной формы, которая должна быть симметрична и положительно-полуопределена.
Метод Баранкина-Дорфмана непосредственно основан на применении теоремы Куна-Такера, поэтому условие Куна-Такера в матричной форме для КП выглядит следующим образом:
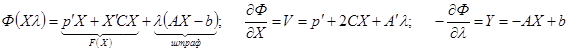
Тогда условие Куна-Такера можно записать в следующем виде:
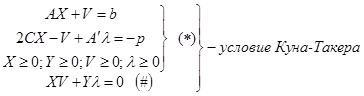
Неизвестными являются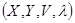 
.
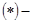система линейных уравнений относительно неизвестных; решить её, значит найти решение задачи ЛП. 
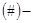нелинейное условие, и поэтому задача сводится к нахождению точки в допустимой области, чтобы выполнилось 
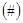. Введём новый вектор 
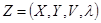и 
.
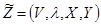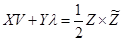
Окончательно условие Куна-Такера будет выглядеть так:
Метод Баранкина-Дорфа заключается в следующем: находится допустимый вектор 
, удовлетворяющая выражению (1) и проверяется условие (2). Далее выбирается новое базисное решение, причём оно выбирается так, чтобы величина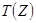 
всё время уменьшалась. Для этого используется модифицированная симплекс-таблица, в которой генеральный элемент находится минимизацией выпуклой функции :
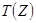т. е. мы решаем задачи (1) и (3), а не (1) и (2). В симплекс-таблице записывается в качестве базисных переменных, все переменные. Запишем строку базисных переменных:
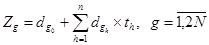
где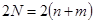 
и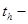 
свободные переменные.
Если строка соответствует свободным переменным, то в строке одна единица и остальные нули. Для выбора генерального элемента используются следующие элементы, которые записываются в дополнительные строки:
Можно показать, что новое значение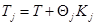 
: По определению 
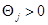, поэтому 
должно быть меньше нуля, так как хотим, что бы оно было меньше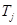 
. Рассмотрим величину : величина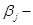 
вторая производная функции 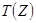, которая выпукла вниз, и поэтому 
, значит, надо выбрать тот столбец для которого 
, а строку надо выбрать ту, для которой вычисляется величина 
.
Пример:
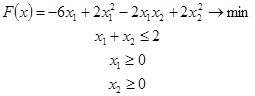
Запишем все матрицы, которые нам нужны:
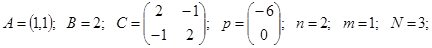
Запишем условие Куна-Такера, определяемое выражением (1):
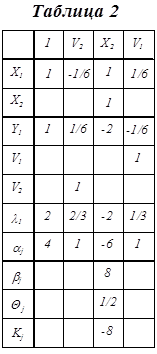
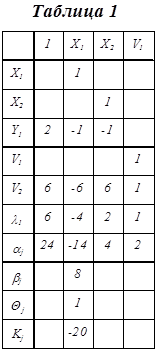
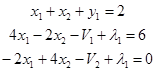
Чтобы записать симплекс-таблицу надо выделить базис. Для получения первого базисного решения используется любой метод, например, метод Гаусса. Можно использовать метод, который использует симплекс-процедуры. Для любых задач можно и подобрать первое базисное решение. Мы подберём такое, чтобы сразу получить опорное решение:
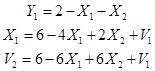
Запишем симплекс-таблицу по методу Баранкина-Дорфмана – таблица 1.
Симплекс преобразования: строку умножаем на 
, а столбец на 
. Порядок строк нарушать нельзя.
Недостаток метода: иногда встречаются задачи, когда все 
. Значит мы будем переходить в новую вершину и значение будет увеличиваться, т.е. в соседних вершинах значение больше (мы идём по соседним вершинам в симплекс-методе). В этом случае идём на временное ухудшение 
, т.е. идём через «мёртвую зону». В алгоритме Франца-Вольфа это учтено.
