Если априорная информация неизвестно или ненадёжна, то применяются другие критерии:
1) Критерий Вальда 
: это максимально-минимальный критерий, т. е. выбирается максимальная стратегия 
, для которой 
. Мы подходим к.той задаче, рассчитывая на самый худший случай, как и в игре с разумным противником.
2) Критерий Сэвиджа 
: это критерий минимаксного риска: 
. Этот критерий не эквивалентен критерию Вальда, т. е. оптимальный по Сэвиджу не обязательно так же будет эквивалентен по Вальду.
3) Критерий Гурвица 
: это комбинированный критерий, его так же называют критерием пессимизма-оптимизма: 
; 
коэффициент, который выполняет требования критерия быть более или менее оптимистичным. При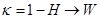 
, а при 
, 
крайний оптимизм.
Существуют другие критерии и однозначный выбор одного критерия невозможен. Но если одну и ту же ситуацию рассматривать по разным критериям, то получается одинаковое решение по разным критериям.
Планирование эксперимента в условиях
Неопределённости.
Если априорной информации нет или она ненадёжна, то можно путём проведения эксперимента получить более надёжные данные о вероятности 
. Под экспериментом понимают систему мероприятий позволяющих уточнить информацию о состоянии природы. Насколько может помочь в принятии решения эксперимент и как сопоставить стоимость эксперимента с тем оптимальным выигрышем, который мы получим?
Соответствующую теорию можно построить исходя из знания вероятности , а так же из знания на основе критериев при неизвестной априорной информации. Мы рассмотрим когда есть априорная информация, т. е. ситуацию идеального наблюдателя. Появляется вопрос: есть ли смысл проводить эксперимент? Возможны два случая:
1) Идеальный эксперимент. Результат этого эксперимента однозначно определяет каковы условия природы. Пусть заданы выигрыши 
и априорные вероятности . Стоимость эксперимента сопоставима с , т. е. имеют одинаковую размерность. Сравним средний выигрыш без проведения эксперимента со средним выигрышем при проведении эксперимента:
Нет эксперимента: 
Если мы проведём эксперимент, то мы точно узнаем 
, и тогда найдя в 
ом столбце максимальный выигрыш, мы найдём наш выигрыш: 
.
Но нам нужно оценить эффективность эксперимента до его проведения, поэтому мы должны ориентироваться на средний ожидаемый выигрыш, который мы получим, если будем проводить эксперимент. Таким образом, после эксперимента мы можем ожидать выигрыш 
. Поэтому чтобы решить, проводить эксперимент или нет, надо определить, что больше: 
или 
. Получается, что мы будем проводить эксперимент, если:
B преобразовав это неравенство, получим:
2) Неидеальный эксперимент. В результате проведения эксперимента мы не находим однозначно 
, а лишь изменяем вероятность 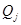. Пусть проводится неидеальный эксперимент. В результате появляются некоторые несовместные события 
. Вероятности этих событий зависят от условий, в которых они проводятся. Пусть известны 
. Эти вероятности называются прямыми. После эксперимента, давшего исход 
необходимо пересмотреть вероятности 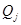, т. е. вместо вероятности 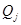мы перейдём к вероятности 
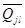. Это так называемые апостериорные вероятности:
Формула Байеса.
Но результаты эксперимента могут быть 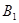и 
и 
и 
, поэтому мы можем только ожидать всякие исходы , которые получатся в результате эксперимента. Причём, каждый исход привёл бы к некоторым оптимальным стратегиям 
. А величина выигрыша, которая бы при этом получилась:
Эти выигрыши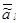 
, могут произойти с вероятностью события , т. е. это вероятность 
. У нас их нет, но их можно получить по формуле полной вероятности:
Тогда ожидаемый выигрыш будет:
Можно рассмотреть случай, когда проводят 
эксперимента. Их при этом считают независимыми.
