Термомеханический эффект состоит в возникновении разности давлений dp=p 2 —p 1 в резервуарах с жидкостью, соединенных капилляром, при поддержании в них разности температур dT = T 2 — T 1. В случае, когда резервуары отделены один от другого пористой перегородкой, этот эффект называется термоосмосом. Мы уже рассматривали его для ультраразреженного газа.
Явление, обратное термомеханическому эффекту, т. е. появление разности температур в результате создания разности давлений в сосудах, называется механокалорическим эффектом.
Рассмотрим теорию этих двух необратимых явлений. Пусть два сосуда 1 и 2 поддерживают при постоянных температурах Т и T+dT. Обозначим: I 1 — поток энергии между сосудами, I 2 — возможный поток вещества. Соответствующие этим потокам силы, согласно формуле (14.28), равны (хотя это и не очевидно, приведем формулы без доказательства)
.
По линейному закону
В стационарном состоянии поток I 2 равен нулю, а поток энергии I 1 остается постоянной величиной. Поэтому из формул получаем
,
.
Для однокомпонентной жидкости
,
где V и H – объем и энтальпия (энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении) моля жидкости.
.
Из этого выражения видно, что термомеханический эффект будет существовать только тогда, когда молярная энтальпия жидкости не равна дроби 
. Для выяснения смысла этой дроби рассмотрим два сосуда при одинаковой температуре (сила X 1 равна нулю). Тогда из уравнения получаем
,
то есть 
– энергия переноса (энергия, перенесенная единицей массы из сосуда 1 в 2 при изотермическом процессе).
При таком переносе энергии в сосуде 1 поддерживаются постоянными температура Т и давление р за счет поглощения теплоты Q* от внешнего теплоисточника и совершения работы. Поэтому изменение внутренней энергии жидкости в сосуде 1 при выходе из него моля жидкости по первому началу равно
,
откуда 
.
Количество теплоты ,поглощенное в сосуде 1 молем жидкости, перенесенной из сосуда 1 в сосуд 2 при постоянных температуре и разности давлений, называется теплотой переноса. Таким образом,
(1)
и, следовательно, при положительном значении Q* в стационарном состоянии более высокое давление устанавливается там, где более низкая температура.
Ранее мы рассматривали эффект Кнудсена для стационарного состояния разреженных идеальных газов с разной температурой в двух сосудах, соединенных малым отверстием. Очевидно, что это частный случай вышеприведенного рассмотрения. На основании кинетической теории можно найти, что энергия переноса на моль газа равна
,
а молярная энтальпия
.
Поэтому теплота переноса
(2)
имеет отрицательноезначение.
Подставляя выражение (2) в (1), получим соотношение Кнудсена:
т. e. при соединении капилляром двух сосудов с ультраразреженными газами (длина свободного пробега молекул больше размеров сосуда) с разной температурой давление будет больше в том сосуде, который горячее.
В обычном случае идеального газа, т. е. когда отверстие между сосудами так велико, что газ проходит макроскопическим потоком, энергия переноса U* включает кроме внутренней энергии U еще и работу pV, так что
.
10. Поверхностное натяжение. Капиллярные явления
Свободная поверхностная энергия.
Жидкое состояние возникает тогда, когда потенциальная энергия притяжения молекул превосходит по абсолютному значению их кинетическую энергию. Силы притяжения между молекулами в жидкости значительны и обеспечивают удержание молекул в объеме жидкости. Таким образом, у жидкости образуется поверхность, которая ограничивает ее объем. Разберемся, какой будет эта поверхность, которая, очевидно, зависит от формы объема жидкости.
Жидкости занимают промежуточное состояние между газами и кристаллами и сочетают в себе некоторые свойства обоих этих состояний. В жидкостях имеет место так называемый ближний порядок: относительно рассматриваемой молекулы упорядоченно располагаются лишь ближайшие соседи, отстоящие на расстоянии 2-3 межатомных интервалов. Примерно на такое же расстояние распространяется заметное взаимодействие между молекулами.
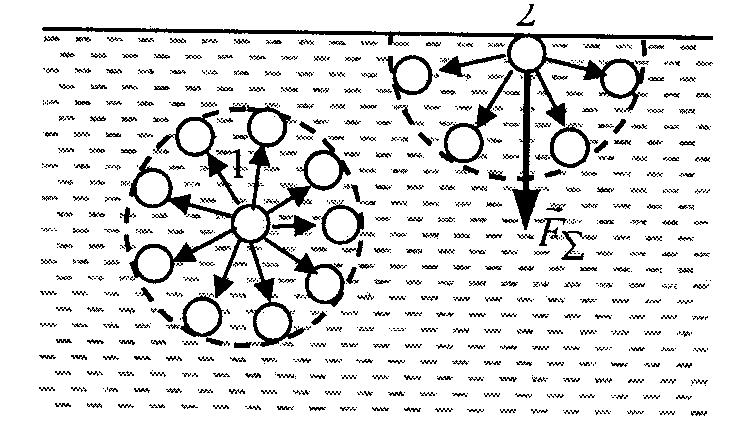Молекулу 1, находящуюся внутри жидкости, ближайшие соседи окружают со всех сторон. Она испытывает притяжение со стороны всех соседних с ней молекул. При этом их притяжение взаимно компенсируется. Молекулу 2, находящуюся у поверхности жидкости, ближайшие соседи окружают только с одной стороны. На такие частицы вблизи поверхности жидкости со стороны других молекул жидкости действуют силы, равнодействующая которых направлена внутрь жидкости, нормально к поверхности. Эта сила консервативная, поэтому при перемещении молекулы из какой-либо внутренней точки жидкости в точку поверхностного слоя эта сила совершает работу А, которая равна приращению потенциальной энергии молекулы:
.
Так как A <0 (работу нужно затратить), то Wp 2 > Wp 1.
Таким образом, каждая молекула, находящаяся на поверхности жидкости, обладает избыточной потенциальной энергией по сравнению с молекулами, находящимися внутри жидкости.
Поскольку всякая система стремится перейти в состояние с минимальной потенциальной энергией, то жидкость (под действием втягивающих сил) принимает такую форму, при которой площадь ее поверхности минимальна. При отсутствии других сил (например, в невесомости) такой фигурой является шар. Если жидкость находится в поле сил тяготения, то она принимает форму, соответствующую минимуму суммарной энергии – в поле сил тяготения и поверхностной энергии.
Если мы рассмотрим маленькую каплю, то ее поверхностная энергия (пропорциональная площади поверхности, определяемой квадратом линейных размеров) будет больше, чем энергия в поле сил тяготения (которая пропорциональна объему тела, то есть кубу линейных размеров). Поэтому маленькие капли принимают близкую к сферической форму. Но при увеличении объема начинает преобладать энергия в поле сил тяготения, поэтому капли сплющиваются под действием сил тяжести.
Свойство жидкости сокращать свою свободную поверхность называется поверхностным натяжением. Коэффициент поверхностного натяжения – СФВ, характеризующая свойство жидкости сокращать свою свободную поверхность, и равная отношению модуля силы поверхностного натяжения, действующей на границу поверхностного слоя, к длине этой границы:
.
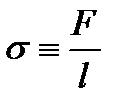Оно зависит от свойств жидкости и варьируется в широких пределах. У большинства жидкостей поверхностное натяжение имеет при 20°С порядок от 10-2 до 10-1 Н/м.
Механизм возникновения поверхностного натяжения. Свободная энергия, характеризуемая σ, сосредоточена в небольшом поверхностном слое жидкости, поэтому и силы поверхностного натяжения действуют только в тонком поверхностном слое. В этом отношении тонкий поверхностный слой действует наподобие резиновой оболочки, которой окружен объем жидкости. Разница с резиновой оболочкой состоит лишь в том, что она имеет постоянное натяжение независимо от того, как изменяется поверхность жидкости в результате изменения формы занимаемого ею объема.
Поверхностное натяжение зависит от свойств вещества, с которым соприкасается поверхность жидкости. Это особенно очевидно из интерпретации σ как плотности свободной энергии, поскольку вещество у поверхности жидкости также воздействует на молекулы поверхностного слоя жидкости и, следовательно, изменяет силы, втягивающие их внутрь жидкости. Это означает, что поверхностное натяжение σ изменяется. Поэтому, когда идет разговор о поверхностном натяжении, надо указывать не только жидкость, которая имеется в виду, но и вещество, с которым поверхность жидкости соприкасается, т. е. σ должна быть снабжена двумя индексами, указывающими две граничащие между собой среды. Ясно, что поверхностное натяжение на поверхности раздела двух жидкостей должно быть меньше, чем на свободной поверхности. На поверхности раздела твердого тела с жидкостью поверхностное натяжение также уменьшается.
Условия равновесия на границе двух жидкостей. Если на поверхность одной жидкости поместить каплю другой, более легкой, то возможны два результата в зависимости от соотношения поверхностных натяжений. Если обозначить dl элемент длины, направленный вдоль линии соприкосновения трех сред 1, 2, 3, то силы поверхностного натяжения, действующие на этот элемент, равны σ 12 dl, σ 23 dl, σ 13 dl. Заметим, что элемент dl направлен перпендикулярно плоскости чертежа. Если σ 13 < σ 23 + σ 12 то равновесие реализуется в виде ситуации, изображенной на рис. 78, а. Условием равновесия является обращение в нуль равнодействующих всех сил, действующих на элемент dl:
Система этих уравнений позволяет определить углы 
и 
, которые называются краевыми.
Если же σ 13 > σ 23 + σ 12, то равновесная ситуация указанного вида невозможна и капля 2 растечется по всей поверхности жидкости 1 в виде тонкого молекулярного слоя
Условия равновесия на границе жидкость — твердое тело.
В этом случае возможны равновесные ситуации, показанные на рис. Условия равновесия при этом имеют соответственно вид
Если σ 13 > σ 23 + σ 12, то жидкость растекается по поверхности молекулярным слоем. Это случай полного смачивания. На первом рисунке приведен пример частичного смачивания, на втором – полного несмачивания.
Если жидкость налита в сосуд, то форма жидкости при соприкосновении с вертикальными стенками сосуда различна в зависимости от того, смачивает жидкость стенки сосуда или не смачивает.
Если краевой угол удовлетворяет условию 0 < Θ < 90, имеет место частичное смачивание жидкостью поверхности твердого тела. В этом случае силы взаимодействия между молекулами жидкости и твердого тела больше сил взаимодействия между молекулами жидкости. Если 90 < Θ < 180, имеет место частичное несмачивание жидкостью поверхности твердого тела. В этом случае силы взаимодействия между молекулами жидкости и твердого тела меньше сил взаимодействия между молекулами жидкости.
При плавании тел в жидкости из-за эффектов смачивания и несмачивания возникают дополнительные силы, которые либо увеличивают подъемную силу, либо уменьшают ее. Когда жидкость смачивает твердое тело, то поверхностное натяжение направлено против подъемной силы и стремится погрузить тело в жидкость. Когда жидкость не смачивает твердое тело, поверхностное натяжение направлено вверх и стремится вытолкнуть тело из жидкости. Эти дополнительные силы за счет поверхностного натяжения обычно невелики по сравнению с силами Архимеда. Но бывают ситуации, когда они существенны. Например, если плотность плавающего тела лишь незначительно превосходит плотность жидкости, а его линия соприкосновения с поверхностью жидкости достаточно велика, то может случиться, что тело не утонет исключительно из-за поверхностного натяжения, если тело не смачивается жидкостью. Известны насекомые, которые бегают по поверхности воды и при этом не тонут за счет поверхностного натяжения воды.
Давление под искривленной поверхностью. Формула Лапласа.
Искривленный поверхностный слой оказывает на жидкость дополнительное давление. (Такое искривление называется мениском.)
В случае выпуклого мениска поверхностный слой, стремясь сократиться, сжимает жидкость, в случае вогнутого мениска – растягивает ее. Рассмотрим простейший случай, когда жидкость находится в вертикальной цилиндрической трубке радиуса r и не смачивает ее стенки. Мениск в этом случае представляет собой полусферу, обращенную выпуклостью вверх. Сила давления поверхностного слоя, действующая на жидкость, направлена вертикально вниз и равна по модулю F =2 πrσ. Для нахождения добавочного давления эту силу нужно разделить на площадь поперечного сечения трубки πr 2. В результате получим:
.
Формула называется формулой Лапласа, а давление pЛ – лапласовым давлением. Под выпуклым мениском лапласово давление положительно, под вогнутым – отрицательно.
Приведем вывод формулы Лапласа для случая мыльного пузыря. Резиновый шар или мыльный пузырь могут оставаться в равновесии, только если давление внутри них на определенную величину больше, чем давление снаружи. Вычислим это превышение. Пусть мыльный пузырь имеет радиус R и пусть избыток давления внутри него равняется p.
Чтобы увеличить объем пузыря на малую величину dV, нужно затратить работу pdV, которая идет на увеличение энергии поверхности пузыря. Можно показать, что коэффициент поверхностного натяжения имеет смысл энергии, приходящейся на единицу поверхности жидкости. Увеличение энергии в таком случае равно:
,
где σ – коэффициент поверхностного натяжения. (Коэффициент 2 в формуле появляется потому, что у пузыря две поверхности). Таким образом, получим:
.
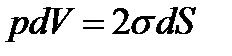Имея в виду, что
и 
,
Получим:
.
У капли будет одна поверхность, соответственно для нее получим формулу с коэффициентом 2.
В общем случае отсутствия сферической симметрии кривизна поверхности определяется двумя главными радиусами кривизны R 1 и R 2. При этом давление дается выражением
.
(средняя кривизна поверхности)
Капиллярные явления.
При взаимодействии со стенкой сосуда силы поверхностного натяжения стремятся либо поднять уровень жидкости, либо опустить его. Если стенки трубки смачиваются жидкостью, то жидкость в ней поднимается, если не смачиваются, то опускается.
Выведем формулу для высоты h, на которую поднимается жидкость в капилляре в случае смачивания. Давление в капилляре на уровне свободной поверхности жидкости в широком сосуде равно атмосферному. Но в капилляре из-за поверхностного натяжения есть капиллярное/лапласово давление. Поэтому между жидкостью в капилляре и широком сосуде устанавливается такая разность уровней h, чтобы гидростатическое давление уравновешивало капиллярное:
.
Окончательно получаем:
.
Радиус кривизны мениска r можно выразить через краевой угол и радиус капилляра R. Из рисунка видно, что 
. Следовательно,
.
Чем меньше радиус трубки, тем выше поднимается по ней жидкость в случае смачивания. Поэтому такой эффект называется капиллярным.
Одним из механизмов подъема воды деревьями является как раз капиллярный.
[1] В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия). В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
[2] При движении под действием центральной силы момент вектора скорости v относительно центра О будет величиной постоянной. По сути, следствие закона сохранения момента импульса в поле центральной силы.
[3] Коэффициент пропорциональности k T/h, где h – постоянная Планка.
