Лекция 1.3.1 «Системы линейных алгебраических уравнений: общая теория»
Учебные вопросы:
1. Системы линейных алгебраических уравнений.
Теорема Кронекера - Капелли
2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
Системы линейных алгебраических уравнений. Теорема Кронекера - Капелли
Рассмотрим систему m линейных алгебраических уравнений с n неизвестными 
:
Здесь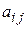 
- коэффициенты системы (
- номер уравнения (строки), 
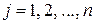- номер неизвестной, при которой данный коэффициент стоит), 
- свободные члены системы. Если все свободные члены равны нулю (
, ), то система называется однородной, в противном случае - неоднородной. Если не оговорено особо, будут рассматриваться неоднородные системы.
Система может не иметь решений (уравнения несовместны), иметь единственное решение (единственный набор значений неизвестных ), иметь бесчисленное множество решений.
Составим из коэффициентов 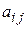при неизвестных матрицу
и назовем ее матрицей системы. Матрицу 
называют матрицей-столбцом из свободных членов, а матрицу 
– матрицей-столбцом из неизвестных. Матрицу 
, полученную из матрицы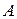 
добавлением столбца свободных членов, называют расширенной матрицей системы:
.
Теорема Кронекера - Капелли: система m линейных алгебраических уравнений с n неизвестными имеет решение в том и только в том случае, если матрица системы и расширенная матрица системы имеют один и тот же ранг 
. В противном случае уравнения несовместны.
Единственное решение существует, если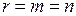 
.
Если обе матрицы имеют ранг 
,то уравнения системы линейно зависимы и некоторые 
можно выразить в виде линейных комбинаций остальных уравнений (независимых), и им удовлетворяют решения этих уравнений. Линейно независимые уравнения определяют некоторые неизвестных как линейные функции остальных 
неизвестных, остающихся произвольными.
Если обе матрицы имеют ранг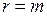 
,то уравнения системы линейно независимы.
Пример. Исследовать систему линейных уравнений
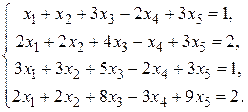
◄ Составим расширенную матрицу системы и с помощью указанных около нее элементарных преобразований найдем одновременно ранги обеих матриц:
Прибавив к четвертой строке последней матрицы третью строку, получаем
.
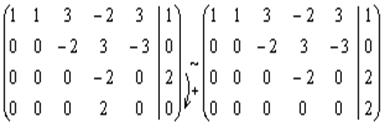Ранг матрицы системы равен трем, так как ее преобразованная матрица имеет три ненулевых строки, а ранг расширенной матрицы равен четырем. Тогда согласно теореме Кронекера-Капелли система не имеет решений. ►
