Если общее уравнение (5.17) задает невырожденную кривую второго порядка, то оно может быть приведено к каноническому виду введением новой системы декартовой координат, совершив поворот осей на определенный угол и подходящий перенос начала.
При переносе начала координат (параллельный перенос осей) координаты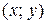 
точки плоскости в исходной системе координат (старой) и координаты 
этой же точки в преобразованной системе (новой) связаны следующими формулами преобразования:
(5.22)
где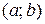 
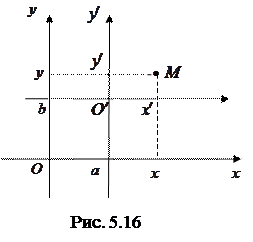
– координаты нового начала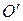 
относительно исходной системы (рис. 5.16). Формулы преобразования (5.22) справедливы, только если на осях обеих систем выбраны одинаковые единицы масштаба.
Если в общем уравнении кривой второго порядка (5.17) коэффициент 
при произведении координат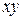 
равен нулю
(
), то оси исходной системы координат параллельны осям симметрии этой кривой, и для приведения уравнения к каноническому виду необходимо только произвести подходящий параллельный перенос осей в новое начало. Это можно сделать выделением в уравнении полных квадратов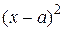 
и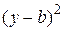 
с последующим переносом начала координат в точку 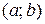по формулам преобразования (5.22).
Пример. Привести уравнение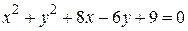 
к каноническому виду и построить задаваемую этим уравнением кривую.
◄ В данном уравнении коэффициенты , 
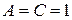, следовательно, оно может задавать окружность. Выделяем в уравнении полные квадраты: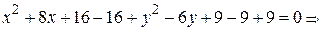 
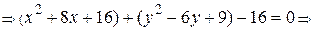
. Заменой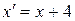 
, 
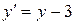приводим уравнение к каноническому виду 
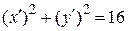, которое задает на плоскости окружность радиуса 
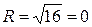. Центр этой окружности находится в начале 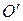новой системы координат 
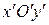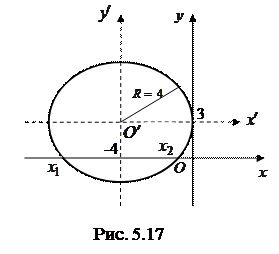
, а в исходной системе этот центр находится в точке с координатами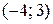 
(рис. 5.17). Окружность касается оси 
в точке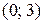 
. Точки пересечения окружности с осью 
получим, положив в исходном уравнении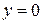 
и решив получающееся квадратное уравнение 
: 
, 
►
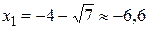Если в общем уравнении кривой второго порядка (5.17) коэффициент при 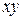не равен нулю, то оси координат не параллельны осям симметрии кривой второго порядка. Для того чтобы сделать эти оси параллельными, необходимо повернуть оси координат на угол 
, который равен в исходной системе координат углу между положительным направлением оси и каждой из осей симметрии кривой. Этот угол определяется формулой
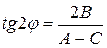. (5.23)
При повороте осей (рис. 5.18) координаты точки плоскости 
в преобразованной системе координат (новой) и координаты 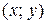этой же точки в исходной системе (старой) связаны следующими формулами преобразования:
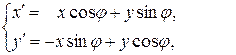(5.24)
Обратное преобразование имеет вид:
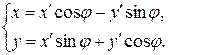(5.25)
Если ввести матрицы 
, 
, 
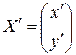, то преобразование (5.24) можно записать в матричной форме:
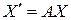
Обратное преобразование (5.25) в матричной форме будет иметь вид:
,
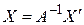где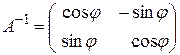 
– матрица, обратная матрице 
.
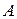Пример. Построить кривую, заданную уравнением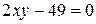 
.
◄ Для данного уравнения второго порядка коэффициенты (см. 5.17) 
, 
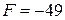, все остальные равны нулю. Находим инварианты кривой: 
, 
, 
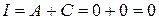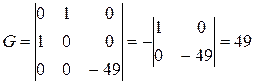. Так как 
, 
, 
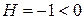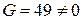, делаем вывод, что данное уравнение задает гиперболу, оси симметрии которой не параллельны осям координат, и для приведения уравнения к каноническому виду необходим поворот осей координат. Необходимый угол поворота определяем по формуле (5.23). Так как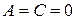 
, знаменатель дроби в этой формуле обращается в нуль, следовательно, 
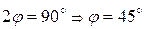. При повороте осей координат на угол 
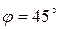переход от старых координат к новым будет задаваться согласно (5.25) следующими формулами преобразования:
Заменяя в исходном уравнении старые координаты на новые, будем иметь: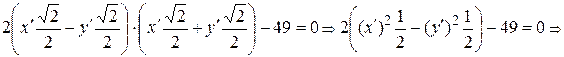 
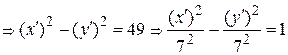. Последнее уравнение есть каноническое уравнение гиперболы в повернутой системе координат. Для этой гиперболы 
, 
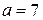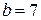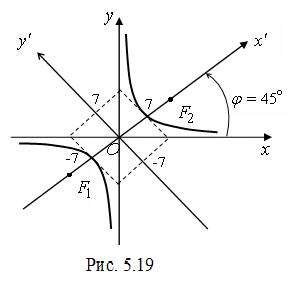
, половина фокусного расстояния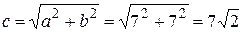 
. На рис. 5.19 представлены старая и новая система координат с построенной в ней по каноническому уравнению гиперболой. ►
