Макроэкономика функционирования многоотраслевой экономики требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны является производителем, а с другой – потребителем продукции, выпускаемой другими отраслями.
Принципиальная схеме многоотраслевого баланса производства и распределении совокупного продукта в стоимостном выражении может быть построена следующим образом.
Будем предполагать, что производственная сфера хозяйства представляет собой n отраслей, каждая из которых производит свой однородный продукт. Для обеспечения производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Рассмотрим процесс производства за некоторый период (например, за год).
Обозначения:
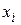- общий объем продукции i отрасли (ее валовый выпуск);
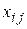- объем продукции i отрасли, потребляемой j отраслью при производстве продукции объема 
.
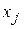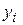- объем продукции i отрасли, предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления).
Часть объема продукции 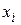, произведенная i -ой отраслью используется для собственного производства в объеме 
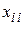, часть – поступает в остальные отрасли для потребления при производстве в объемах (
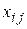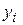), и некоторая часть объемом – для потребления в непроизводственной сфере, так называемый объем конечного потребления.
При балансе отраслевых связей валовой выпуск i -ой отрасли должен быть равен сумме объемов продукции, потребляемых в производственной и непроизводственной сферах, т. е.
, 
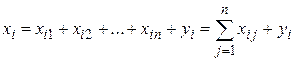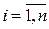. (6.4)
Уравнения (6.4) называются соотношениями (уравнениями) баланса.
Введем коэффициенты прямых затрат по формуле
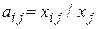, (6.5)
выражающие затраты продукции i -ой отрасли на производство единицы продукции j -ой отрасли.
Будем считать сложившиеся технологии производства во всех отраслях неизменными за рассматриваемый период времени и. следовательно, коэффициенты прямых затрат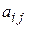 
постоянными. Используя 
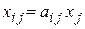, уравнения баланса можно записать в виде
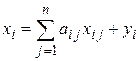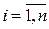, . (6.6)
Введя вектор валового выпуска X (режим работы отраслей), матрицу прямых затрат A и вектор конечного потребления Y: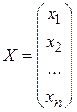 
, 
, 
,
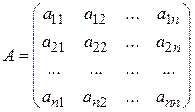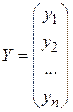уравнения баланса можно записать в матричной форме
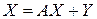. (6.7)
Уравнения (6.6) и (6.7) называются уравнениями межотраслевого баланса или линейной моделью Леонтьева (в честь американского ученого В. Леонтьева, который их впервые получил и подробно изучил в 1936 г.).
В модели Леонтьева можно выполнять три типа расчетов планирования производства:
1) зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции для всех отраслей (вектор конечного потребления)
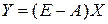; (6.8)
2) задавая величины конечной продукции всех отраслей Y можно определить величину валовой продукции каждой отрасли
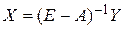; (6.9)
3) задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.
Из экономического смысла параметров, входящих в уравнения (6.6), следует, что матрицы (векторы) X, Y и матрица А, которую называют еще технологической или структурной матрицей) должны быть положительными (т. е. должны быть положительны их элементы: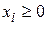 
, 
, 
, 
.
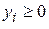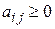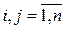Рассмотрим вопрос о разрешимости уравнения (6.8) и, следовательно, уравнения (6.7).
Если матрица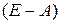 
невырожденная, т. е. ее определитель 
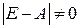, то уравнение (6.8) имеет единственное решение (6.9), где обратная матрица 
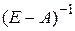называется матрицей полных материальных затрат. Каждый элемент этой матрицы выражает величину выпуска продукции i -ой отрасли, необходимого для производства единицы конечного продукта j -ой отрасли 
, 
.
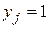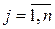Рассмотрим условия (критерии) существования положительных решений матричного уравнения (6.7).
Матрица прямых затрат A с неотрицательными элементами 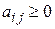, 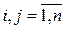называется продуктивной матрицей, если существует такой вектор валового выпуска X > 0, для которого выполняется неравенство X > AX. Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX > 0.
Модель Леонтьева с продуктивной матрицей A называется продуктивной моделью.
Теорема. Для того чтобы матрица А была продуктивной, необходимо и достаточно, чтобы элементы матрицы 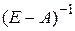были неотрицательны.
Пример. В таблице приведены данные (в ден. ед.) об исполнении баланса между двумя отраслями за некоторый период времени:
Таблица
| Отрасль | Внутрипроизводственное потребление | Валовой продукт | Конечный продукт | |
| Энергетика | ||||
| Машиностроение |
Вычислить:
1) Величину конечного продукта, если валовой выпуск составил бы
;
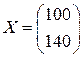Необходимый объем валового выпуска отраслей, если объем конечного потребления увеличить до уровня 
.
◄ Используя данные таблицы и формулу (6.5), получим матрицу прямых затрат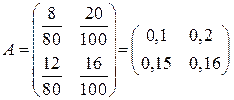 
, а затем матрицу полных затрат 
.
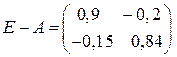1) Вектор конечного продукта находим по формуле (6.8):
.
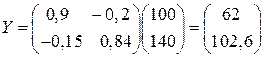2) Вычисляем определитель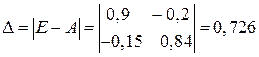 
. Так
как он оказался отличным от нуля делаем вывод, что матрица 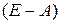невырожденная и имеет обратную. Находим эту обратную матрицу: 
.
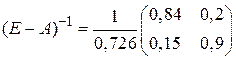Все элементы полученной обратной матрицы оказались неотрицательными и, следовательно, в соответствие с приведенной выше теоремой матрица А продуктивна и решение уравнения (6.8) положительно при любых значениях конечного продукта, в частности, и при :
.
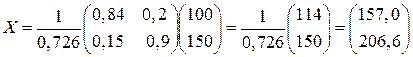Таким образом, чтобы обеспечить конечный продукт в объеме , валовой выпуск в энергетической отрасли нужно увеличить до 157,0 ден. ед., а в машиностроительной - до 206,6 ден. ед. На рисунке приведена схема баланса производства и распределения совокупного продукта для обеспечения такого конечного продукта. ►
Раздел II: Математический анализ
