Канонические уравнения эллипса, гиперболы, параболы

Кривые второго порядка определяются уравнениями второй степени относительно декартовых прямоугольных координат. Общее уравнение второй степени относительно и имеет вид:

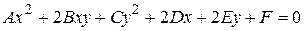. (5.17)

Для любого уравнения (5.17) три величины

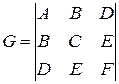, , (5.18)

сохраняются при переносе и повороте осей координат (являются инвариантами). Эти инварианты определяют свойства кривой второго порядка, не зависящие от ее положения на плоскости.

Классификация кривых второго порядка, основанная на их инвариантах:

1) эллипс при , ;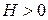

2) окружность пр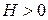и , , или , ;

3) точка (эллипс, выродившийся в точку) при , ;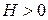

4) ни одной действительной точки при , ;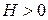

5) гипербола при ;

6) пара пересекающихся прямых (выродившаяся гипербола) при , ;

7) парабола при ;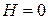

8) пара параллельных прямых или одна прямая (пара совпавших прямых) или ни одной действительной точки при , .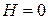

Таким образом, уравнение (5.17) может задавать эллипс (частный случай – окружность), гиперболу, параболу (невырожденные кривые второго порядка) или пустое множество точек, одну точку, одну прямую, пару прямых (вырожденные кривые).

Уравнение кривой второго порядка подходящим переносом начала отсчета и поворотом осей координат может быть приведено к каноническому (или стандартному) виду.

Эллипс – геометрическое место точек (ГМТ), сумма расстояний которых до двух данных точек и , называемых фокусами, есть величина постоянная. Если оси прямоугольной системы координат направлены по осям симметрии эллипса (рис. 5.12), то его уравнение принимает следующий стандартный вид (каноническое уравнение эллипса):

, (5.19)

где – фиксированная сумма расстояний фокусов и до любой точки эллипса (см. рис. 5.12), – расстояние между фокусами (фокусное расстояние), . Отрезки и , отсекаемые эллипсом на его осях симметрии, есть длины большой и малой осей эллипса, точки , , и – вершины эллипса, точка – его центр. Величина 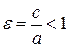называется эксцентриситетом эллипса, а – коэффициентом сжатия эллипса.

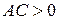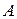Эллипс, центр которого не совпадает с началом координат, но большая и малая оси которого параллельны соответственно осям координат и , задается общим уравнением (5.17), в котором и ( и одного знака).

Если эксцентриситет (оба фокуса находятся в начале координат, т. е. и, следовательно, ), имеем частный случай эллипса – окружность радиуса . Общее уравнение (5.17) при задает окружность, если и . Общее уравнение окружности радиуса можно привести к виду:

,

где точка – центр окружности.

 

Пример. Записать каноническое уравнение эллипса, если сумма расстояний произвольной его точки до фокусов равна 10, а фокусное расстояние равно 8.

◄ По условиям 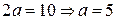, . Находим . Подставляя найденные значения и в (5.19), получаем искомое каноническое уравнение эллипса: . ►

Гипербола – ГМТ, абсолютное значение разности расстояний которых до двух данных точек и , называемых фокусами, есть величина постоянная. Если оси прямоугольной системы координат направлены по осям симметрии гиперболы (рис. 5.13), то ее уравнение принимает следующий стандартный вид (каноническое уравнение гиперболы):

 

, (5.20)

где – фиксированная абсолютная величина разности расстояний фокусов и до любой точки гиперболы (см. рис. 5.13), – расстояние между фокусами (фокусное расстояние), . Отрезок, отсекаемый левой и правой ветвями гиперболы на оси , есть длина действительной оси гиперболы, равная , точки , – вершины гиперболы. Мнимой осью называется ось (ось ), перпендикулярная к действительной оси (ось ). Две прямые, проходящие по диагоналям прямоугольника со сторонами и с центром в центре гиперболы (начале координат) (см. рис. 5.13), являются асимптотами гиперболы. С этими прямыми гипербола неограниченно сближается при неограниченном возрастании абсолютной величины координаты точки гиперболы. Уравнения асимптот гиперболы и . Вершины гиперболы касаются вертикальных противоположных сторон прямоугольника.

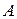Гипербола, центр которой не совпадает с началом координат, но действительная и мнимая оси которой параллельны соответственно осям координат и , задается общим уравнением (5.17), в котором и ( и разных знаков).

Уравнение задает на плоскости гиперболу, сопряженную к гиперболе, уравнение которой имеет вид (5.20). На рис. 5.14 представлены такие сопряженные гиперболы.

 

Пример. Гипербола задана каноническим уравнением . Найти ее фокусное расстояние и расстояние между вершинами (длину действительной оси).

◄ Из уравнения имеем , . Для гиперболы , отсюда для фокусного расстояния будем иметь 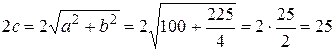. Расстояние между вершинами гиперболы равно . ►

 

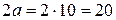Гипербола – ГМТ, равноудаленных от данной точки плоскости , называемой фокусом, и данной прямой , называемой директрисой

(, см. рис. 5.15). В системе координат, центр которой совмещен с вершиной параболы, а ось направлена по оси параболы (рис. 5.15), ее уравнение принимает следующий стандартный вид (каноническое уравнение параболы):

, (5.21)

где – параметр параболы.

Парабола, вершина которой не совпадает с началом координат, но ось которой параллельна оси координат , задается общим уравнением (5.17), в котором и либо либо .

 

Пример. Парабола задана уравнением . Найти параметр параболы .

◄ Заменой данное уравнение приводится к каноническому виду , отсюда имеем . Замена соответствует преобразованию исходной системы координат. Рис. 5.15 позволяет легко понять, что в исходной системе, в которой уравнение имеет вид , ветви параболы направлены вверх (по оси ), ее фокус находится на оси на расстоянии от начала координат, директриса параллельна оси , находясь от нее также на расстоянии ►