Пусть исследуемое предприятие представляет собой двухканальную систему массового обслуживания с ограниченной очередью. На вход поступает пуассоновский поток заявок с интенсивностью λ. Интенсивности обслуживания заявок каждым из каналов μ, а максимальное число мест в очереди m.
Начальные параметры:
Время обслуживания заявок имеет эмпирическое распределение, указанное ниже и имеет среднее значение 
.
Пусть были проведены контрольные замеры времени обработки заявок, поступающих в данную СМО. Чтобы приступить к исследованию, необходимо установить по этим замерам закон распределения времени обработки заявок.
Таблица 61. – Группировка заявок по времени обработки
| Количество заявок | ||||||||
| Время обработки, мин | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 | 25–30 | 30–35 | 35–40 |
Выдвигается гипотеза о показательном распределении генеральной совокупности.
Для того чтобы, при уровне значимости 
проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:
1) Найти по заданному эмпирическому распределению выборочную среднюю 
. Для этого, каждый i – й интервал заменяем его серединой 
и составляем последовательность равноотстоящих вариант и соответствующих им частот.
2) Принять в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней:
(296)
3) Найти вероятности попадания X в частичные интервалы по формуле:
(297)
4) Вычислить теоретические частоты:
, (298)
где 
- объем выборки
5) Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы 
, где S – число интервалов первоначальной выборки.
Таблица 62. – Группировка заявок по времени обработки с усредненным временным интервалом
| Количество заявок | ||||||||
| Время обработки, мин | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | 37,5 |
Найдем выборочную среднюю:
2) Примем в качестве оценки параметра λ экспоненциального распределения величину, равную 
. Тогда:
(
) (299)
3) Найдем вероятности попадания X в каждый из интервалов по формуле:
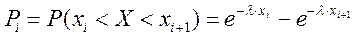(300)
Для первого интервала:
(301)
Для второго интервала:
(302)
Для третьего интервала:
(303)
Для четвертого интервала:
(304)
Для пятого интервала:
(305)
Для шестого интервала:
(306)
Для седьмого интервала:
(307)
Для восьмого интервала:
(308)
4) Вычислим теоретические частоты:
(309)
Результаты вычислений заносим в таблицу. Сравниваем эмпирические 
и теоретические 
частоты с помощью критерия Пирсона.
Для этого вычислим разности 
, их квадраты, затем отношения 
. Суммируя значения последнего столбца, находим наблюдаемое значение критерия Пирсона. По таблице критических точек распределения 
при уровне значимости 
и числу степеней свободы 
находим критическую точку 
Таблица 63. – Результаты вычислений
| i |
| 
| 
|
| 
|
|
| 0,285 | 34,77 | -12,77 | 163,073 | 4,690 | ||
| 0,204 | 24,888 | 0,112 | 0,013 | 0,001 | ||
| 0,146 | 17,812 | 5,188 | 26,915 | 1,511 | ||
| 0,104 | 12,688 | 3,312 | 10,969 | 0,865 | ||
| 0,075 | 9,15 | 4,85 | 23,523 | 2,571 | ||
| 0,053 | 6,466 | 3,534 | 12,489 | 1,932 | ||
| 0,038 | 4,636 | 3,364 | 11,316 | 2,441 | ||
| 0,027 | 3,294 | 0,706 | 0,498 | 0,151 | ||
|
Т.к. 
, то нет оснований отвергнуть гипотезу о распределении X по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой.
Задание 9.
