Пример анализа временных рядов

Покажем последовательность анализа временных рядов на следующем примере. В таблице 56 приведены в относительных единицах данные продаж продовольственных товаров в магазине (Y_t). Разработать модель продаж и провести прогнозирование объема продаж на первые 6 месяцев 1996 года. Выводы обосновать.

Построим график этой функции (рис. 158).

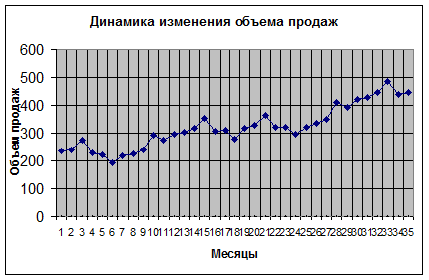
Рис. 158

Анализ графика показывает:

· Временной ряд имеет тренд, весьма близкий к линейному.

· Существует определенная цикличность (повторяемость) процессов продаж с периодом цикла 6 месяцев.

· Временный ряд нестационарный, для приведения его к стационарному виду из него необходимо удалить тренд.

 

После перерисовки графика с периодом 6 месяцев он будет иметь следующий вид (рис.159). Так как колебания объемов продаж достаточно велики (это видно по графику) необходимо провести его сглаживание для более точного определения тренда.

Рис.159

Существует несколько подходов к сглаживанию временного временных рядов:

Ø Простое сглаживание.

Ø Метод взвешенной скользящей средней.

Ø Метод экспоненциального сглаживания Брауна.

Простое сглаживание основано на преобразовании исходного ряда в другой, значения которого являются усредненными по трем рядом стоящим точкам временного ряда:

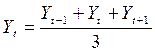(274)

для 1-го члена ряда

(275)

для n -го (последнего) члена ряда

(276)

Метод взвешенной скользящей средней отличается от простого сглаживания тем, что включает параметр w_t, который позволяет вести сглаживание по 5 или 7 точкам

(277)

для полиномов 2-го и 3-го порядков значение параметра w_t определяется из следующей таблицы. Таблицы 57.

m = 5	-3				-3
m = 7	-2						-2

Методы сглаживания временных рядов

Метод экспоненциального сглаживания Браунаиспользует предшествующие значений ряда, взятые с определенным весом. Причем вес уменьшается по мере удаления его от текущего времени

, (278) Таблица 58

 

Месяц	Yt	Y1t	Y2t

где а – параметр сглаживания (1 > a > 0);

(1 - а) – коэф. дисконтирования.

Параметр, а рекомендуется выбирать в пределах от 0,35 до 1.

S_o обычно выбирается равным Y₁ или среднему из первых трех значений ряда.

Проведем простое сглаживание ряда. Результаты сглаживания ряда приведены в таблице 58. Полученные результаты представлены графически на рис.10. Повторное применение процедуры сглаживания к временному ряду позволяет получить более гладкую кривую. Результаты расчетов повторного сглаживания также представлены в таблице 9. Найдем оценки параметров линейной модели тренда по методике, рассмотренной в предыдущем разделе. Результаты расчетов следующие:

Множественный R	0,933302
R-квадрат	0,871052
`a0 = 212,9729043 `t = 30,26026442 `a1 = 5,533978254 `t = 13,50506944 F = 182,3869

 

Уточненный график с линией тренда и моделью тренда представлен на рис. 12.

 

 

Рис. 160. Временной ряд после первого применения
процедуры простого сглаживания (Y_{1 t})

 

Рис.161. Временной ряд после второго применения процедуры простого сглаживания (Y_t2)

Рис. 162

Следующий этап заключается в удалении тренда из исходного временного ряда.

Для удаления тренда вычтем из каждого элемента первоначального ряда значения, рассчитанные по модели тренда. Полученные значения представим графически на рис.163.

Рис. 163

Полученные остатки, как видно из рис. 163, группируются около нуля, а это значит, что ряд близок к стационарному.

Для построения гистограммы распределения остатков рассчитывают интервалы группирования остатков ряда. Количество интервалов определяют из условия среднего попадания в интервал 3-4 наблюдения. Для нашего случая возьмем 8 интервалов. Размах ряда (крайние значения) от –40 до +40. Ширина интервала определяется как 80/8 =10. Границы интервалов рассчитываются от минимального значения размаха полученного ряда

Таблица 59.

-40	-30	-20	-10

Теперь определим накопленные частоты попадания остатков ряда в каждый интервал и нарисуем гистограмму (рис.164).

Рис. 164

Анализ гистограммы показывает, что остатки группируются около 0. Однако в области от 30 до 40 есть некоторый локальный выброс, который свидетельствует о том, что не учтены и не удалены из исходного временного ряда некоторые сезонные или циклически компоненты. Более точно о характере распределения и его принадлежности к нормальному распределению можно сделать выводы после проверки статистической гипотезы о характере распределения остатков. При ручной обработке рядов обычно ограничиваются визуальным анализом полученных рядов. При обработке на ЭВМ существует возможность более полного анализа.

Что же является критерием завершения анализа временного ряда? Обычно исследователи используют два критерия, отличающихся от критериев качества модели при корреляционно-регрессионном анализе.

Первый критерий качества подобранной модели временного ряда основан на анализе остатков ряда после удаления из него тренда и других компонент. Объективные оценки основаны на проверке гипотезы о нормальном распределении остатков и равенстве нулю выборочного среднего. При ручных методах расчета иногда оценивают показатели ассиметрии и эксцесса полученного распределения. Если они близки к нулю, то распределение считается близким к нормальному. Ассиметрия, А рассчитывается как:

(279)

 

В том случае, если A < 0, то эмпирическое распределение несимметрично и сдвинуто вправо. При A > 0 распределение имеет сдвиг влево. При A = 0 распределение симметрично.

Эксцесс, Е. Показатель, характеризующий выпуклость или вогнутость эмпирических распределений

(280)

В том случае, если Е больше или равно нулю, то распределение выпукло, в других случаях вогнуто.

Второй критерий основан на анализе коррелограммы преобразованного временного ряда. В том случае, если корреляции между отдельными измерениями отсутствуют или меньше заданного значения (обычно 0.1) считается, что все компоненты ряда учтены и удалены и остатки не коррелированы между собой. В остатках ряда осталась некая случайная компонента, которая называется «белый шум».

 

 

2.12.1 Модели статистики интервальных данных

В статистике интервальных данных (СИД), в отличии от большинства других статистических и математических методов, элементами выборки являются не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин.

Прежде всего, хочется отметить, что СИД входит в теорию устойчивости или, как принято называть робастности статистических процедур, и примыкает к интервальной математике. В СИД, на данный момент, изучены практически все задачи классической прикладной математической статистики, в частности, задачи регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности и ряд других.

Основная идея СИД является общеинженерной - каждая величина должна приводиться вместе с погрешностью ее определения, к сожалению, эта идея еще не стала общеэкономической, по крайней мере, на уровне экономической теории. Впрочем, достаточно трудно найти «водораздел» где заканчиваются общеинженерные задачи и начинаются общеэкономические.

Для начала, рассмотрим развитие в течение последних 15 лет асимптотических методов статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала надо устремляться к бесконечности объема выборки и только потом - уменьшать до нуля погрешности. Разработана общая схема исследования, включающая расчет двух основных характеристик;

- нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных);

- и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания и статистических выводов, связанных с проверкой гипотез).

Эта схема применена к оцениванию математического ожидания и дисперсии, медианы и коэффициента вариации, параметров гамма-распределения в ГОСТ 11.011-83 и характеристик аддитивных статистик, для проверки гипотез о параметрах нормального распределения, в том числе с помощью критерия Стьюдента, а также гипотезы однородности двух выборок по критерию Смирнова. Разработаны также подходы к учету интервальной неопределенности в основных постановках регрессионного, дискриминантного и кластерного анализов.

Многие утверждения СИД весьма отличаются от аналогов из классической математической статистики. В частности, например, не существует состоятельных оценок: средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии этой оценки, рассчитанной согласно классической теории, и квадрата нотны. Метод моментов иногда оказывается точнее метода максимального правдоподобия. Нецелесообразно с целью повышения точности выводов увеличивать объем выборки сверх некоторого предела. В СИД классические доверительные интервалы должны быть расширены вправо и влево на величину нотны, и длина их не стремится к 0 при росте объема выборки.

СИД позволяет снять некоторые противоречия между метрологией и классической математической статистикой. Например, вторая из названных дисциплин утверждает, что путем увеличения числа измерений можно сколь угодно точно оценить параметр, а первая вполне справедливо оспаривает это утверждение. Результаты СИД уточняют интуитивные представления метрологов (которые сосредотачивались, впрочем, вокруг весьма частного с точки зрения эконометрики вопроса - оценивания математического ожидания) и развенчивают "гордыню" математической статистики.

Очевидно, что это перспективная и быстро развивающаяся область прикладных статистических исследований последних лет, которая может называться - математическая статистика интервальных данных.

Речь идет о развитии методов прикладной математической статистики в часто встречающейся ситуации, когда статистические данные - не числа, а интервалы, в частности, что очень важно, порожденные наложением ошибок измерения на значения случайных величин.

Приведем основные идеи весьма перспективного для вероятностно-статистических методов и моделей принятия решений асимптотического направления в статистике интервальных данных.

В настоящее время признается необходимым изучение устойчивости (робастности) оценок параметров к малым отклонениям исходных данных и предпосылок модели. Однако популярная среди теоретиков модель засорения (Тьюки-Хьюбера) представляется не вполне адекватной для практического применения. Эта модель нацелена на изучение влияния больших "выбросов". Поскольку любые реальные измерения лежат в некотором фиксированном диапазоне, а именно, заданном в техническом паспорте средства измерения, то зачастую выбросы не могут быть слишком большими. Поэтому представляются полезными иные, более общие схемы устойчивости, например, учитываются отклонения распределений результатов наблюдений от предположений модели.

В одной из таких схем изучается влияние интервальности исходных данных на статистические выводы. Необходимость такого изучения была вызвана следующими обстоятельствами. В государственные стандарты СССР по прикладной статистике в обязательном порядке включалось справочное приложение "Примеры применения правил стандарта". При разработке ГОСТ 11.011-83 были переданы для анализа реальные данные о наработке резцов до предельного состояния (в часах). Оказалось, что все эти данные представляли собой либо целые числа, либо полуцелые (т.е. после умножения на 2 становящиеся целыми). Ясно, что исходная длительность наработок искажена. Необходимо учесть в статистических процедурах наличие такого искажения исходных данных. Как это сделать?

Первое, что приходит в голову - модель группировки данных, согласно которой для истинного значения Х проводится замена на ближайшее число из множества {0,5n, n=1,2,3,...}. Однако эту модель целесообразно подвергнуть сомнению, а также рассмотреть иные модели. Так, возможно, что Х надо приводить к ближайшему сверху элементу указанного множества - если проверка качества поставленных на испытание резцов проводилась раз в полчаса. Другой вариант: если расстояния от Х до двух ближайших элементов множества {0,5n, n=1,2,3,...} примерно равны, то естественно ввести рандомизацию при выборе заменяющего числа, и т.д.

Целесообразно построить новую математико-статистическую модель, согласно которой результаты наблюдений - не числа, а интервалы. Например, если в таблице приведено значение 53,5, то это значит, что реальное значение - какое-то число от 53,0 до 54,0, т.е. какое-то число в интервале [53,5 - 0,5; 53,5 + 0,5], где 0,5 - максимально возможная погрешность. Принимая эту модель, мы попадаем в новую научную область - статистику интервальных данных. Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы.

Это направление математики является дальнейшим развитием всем известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции.

В интервальной математике сумма двух интервальных чисел [a,b] и [c,d] имеет вид [a,b] + [c,d] = [a+c, b+d], а разность определяется по формуле [a,b] - [c,d] = [a-d, b-c]. Для положительных значений a, b, c, d произведение определяется формулой [a,b] * [c,d] = [ac, bd], а частное имеет вид [a,b] / [c,d] = [a/d, b/c]. Эти формулы получены при решении соответствующих оптимизационных задач. Пусть х лежит в отрезке [a,b], а у – в отрезке [c,d].

Каково минимальное и максимальное значение для х+у? Очевидно, a+c и b+d соответственно. Минимальные и максимальные значения для х-у, ху, х/у задают нижние и верхние границы для интервальных чисел, задающих результаты арифметических операций.

А от арифметических операций можно перейти ко всем остальным математическим алгоритмам. Так строится интервальная математика.

К настоящему времени удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов. По мнению ряда специалистов, статистика интервальных данных является частью интервальной математики. Впрочем, есть точка зрения, согласно которой такое включение нецелесообразно, поскольку статистика интервальных данных использует несколько иные подходы к алгоритмам анализа реальных данных, чем сложившиеся в интервальной математике.

В настоящей главе развиваем асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, еще в начале 1980-х годов с помощью такой асимптотики были сформулированы правила выбора метода оценивания в ГОСТ 11.011-83.

Разработана общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания и дисперсии, медианы и коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в том числе, с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова.

Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих - оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных, найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия.

Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на показатель качества классификации. Основные идеи и результаты рассматриваемого направления в статистике интервальных данных приведены в публикациях обзорного характера.

Как показала, в частности, международная конференция ИНТЕРВАЛ-92, в области асимптотической математической статистики интервальных данных Россия имеет мировой приоритет. По нашему мнению, со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, "параллельные" обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.

Многие из утверждений статистики интервальных данных весьма отличаются от аналогов из классической математической статистики.

В частности, не существует состоятельных оценок; средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии оценки, рассчитанной согласно классической теории, и некоторого положительного числа (равного квадрату так называемой нотны - максимально возможного отклонения значения статистики из-за погрешностей исходных данных) - в результате метод моментов оказывается иногда точнее метода максимального правдоподобия; нецелесообразно увеличивать объем выборки сверх некоторого предела (называемого рациональным объемом выборки) - вопреки классической теории, согласно которой чем больше объем выборки, тем точнее выводы.

В стандарт был включен раздел, посвященный выбору метода оценивания при неизвестных параметрах формы и масштаба и известном параметре сдвига и основанный на концепциях статистики интервальных данных.

Теоретическое обоснование этого раздела стандарта опубликовано лишь через 5 лет.

Следует отметить, что хотя в 1982 г. при разработке стандарта были сформулированы основные идеи статистики интервальных данных, однако из-за недостатка времени они не были полностью реализованы в ГОСТ 11.011-83, и этот стандарт написан в основном в классической манере. Развитие идей статистики интервальных данных продолжается уже в течение 20 лет.

Ведущая научная школа в области статистики интервальных данных - это школа проф. А.П. Вощинина, активно работающая с конца 70-х годов. Полученные результаты отражены в ряде монографий и статей, в трудах Международных конференций, диссертаций.

В частности, изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.

Необходимо сформулировать сначала основные краеугольные идеи асимптотической математической статистики интервальных данных, а затем рассмотрим реализацию этих идей на перечисленных выше примерах. Следует сразу подчеркнуть, что основные идеи достаточно просты, в то время как их проработка в конкретных ситуациях зачастую оказывается достаточно трудоемкой.

Типовые примеры раннего этапа применения статистических методов описаны в Ветхом Завете (см., например, Книгу Чисел). С математической точки зрения они сводились к подсчетам числа попаданий значений наблюдаемых признаков в определенные градации. В дальнейшем результаты стали представлять в виде таблиц и диаграмм, как это и сейчас делает Росстат РФ. Надо признать, что по сравнению с Ветхим Заветом есть прогресс - в Библии не было таблиц.

Сразу после возникновения теории вероятностей (Паскаль, Ферма, 17 век) вероятностные модели стали использоваться при обработке статистических данных. Например, изучалась частота рождения мальчиков и девочек, было установлено отличие вероятности рождения мальчика от 0.5, анализировались причины того, что в парижских приютах эта вероятность не та, что в самом Париже, и т.д.

В 1794 г. (по другим данным - в 1795 г.) К.Гаусс разработал метод наименьших квадратов, один из наиболее популярных ныне статистических методов, и применил его при расчете орбиты астероида Церера - для борьбы с ошибками астрономических наблюдений. В 19 веке заметный вклад в развитие практической статистики внес бельгиец Кетле, на основе анализа большого числа реальных данных показавший устойчивость относительных статистических показателей, таких, как доля самоубийств среди всех смертей. Интересно, что основные идеи статистического приемочного контроля и сертификации продукции обсуждались академиком Буняковским и применялись в российской армии еще в середине 19 в. Статистические методы управления качеством, сертификации и классификации продукции сейчас весьма актуальны.

Современный этап развития прикладной статистики можно отсчитывать с 1900 г., когда англичанин К.Пирсон основан журнал "Biometrika". Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное (гауссово) распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.

Разработанную в первой трети ХХ в. теорию будем называть параметрической статистикой, поскольку ее основной объект изучения - это выборки из распределений, описываемых одним или небольшим числом параметров. Наиболее общим является семейство кривых Пирсона, задаваемых четырьмя параметрами. Как правило, нельзя указать каких-либо веских причин, по которым конкретное распределение результатов наблюдений должно входить в то, или иное параметрическое семейство.

Исключения хорошо известны: если вероятностная модель предусматривает суммирование независимых случайных величин, то сумму естественно описывать нормальным распределением; если же в модели рассматривается произведение таких величин, то итог, видимо, приближается логарифмически нормальным распределением, и так далее. Однако в подавляющем большинстве реальных ситуаций подобных моделей нет, и приближение реального распределения с помощью кривых из семейства Пирсона или его подсемейств - чисто формальная операция.

Именно из таких соображений не раз критиковал параметрическую статистику академик С. Н. Бернштейн в 1927 г. в своем докладе на Всероссийском съезде математиков. Однако эта теория, к сожалению, до сих пор остается основой преподавания статистических методов и продолжает использоваться основной массой прикладников, остающихся далекими от новых веяний в статистике. Почему так происходит? Чтобы попытаться ответить на этот вопрос, обратимся к наукометрии.

Проведенный в последние десятилетия анализ прикладной статистики как области научно-практической деятельности показал, в частности, что актуальными для специалистов в настоящее время являются не менее чем 100 тысяч публикаций. Реально же каждый из нас знаком с существенно меньшим количеством книг и статей. Так, в известном трехтомнике Кендалла и Стьюарта всего около 2 тысяч литературных ссылок. При всей очевидности соображений о многократном дублировании в публикациях ценных идей приходится признать, что каждый специалист по прикладной статистике владеет лишь небольшой частью накопленных в этой области знаний. Не удивительно, что приходится постоянно сталкиваться с игнорированием или повторением ранее полученных результатов, с уходом в тупиковые (с точки зрения практики) направления исследований, с беспомощностью при обращении к реальным данным, и т.д. Все это - одно из проявлений адаптационного механизма торможения развития науки, о котором еще 30 лет назад писали В. В. Налимов и другие науковеды.

Традиционный предрассудок состоит в том, что каждый новый результат, полученный исследователем - это кирпич в непрерывно растущее здание науки, который непременно будет проанализирован и использован научным сообществом. Реальная ситуация - совсем иная. Основа профессиональных знаний исследователя и инженера закладывается в период обучения. Затем они пополняются в том узком направлении, в котором работает специалист. Следующий этап - их тиражирование новому поколению. В результате вузовские учебники отстоят от современного развития на десятки лет. Так, учебники по математической статистике, по нашей экспертной оценке, в основном соответствуют 40-60-м годам ХХ в. А потому тем же годам соответствует большинство вновь публикуемых исследований и тем более - прикладных работ. Одновременно приходится признать, что результаты, не вошедшие в учебники, независимо от их ценности почти все забываются.

В первой трети ХХ в., одновременно с параметрической статистикой, в работах Спирмена и Кендалла появились первые непараметрические методы, основанные на коэффициентах ранговой корреляции, носящих ныне имена этих статистиков. Но непараметрика, не делающая нереалистических предположений о том, что функции распределения результатов наблюдений принадлежат тем или иным параметрическим семействам распределений, стала заметной частью статистики лишь со второй трети ХХ века. В 30-е годы появились работы А.Н.Колмогорова и Н.В.Смирнова, предложивших и изучивших статистические критерии, носящие в настоящее время их имена.

Эти критерии основаны на использовании так называемого эмпирического процесса - разности между эмпирической и теоретической функциями распределения, умноженной на квадратный корень из объема выборки. В работе А.Н.Колмогорова 1933 г. изучено предельное распределение супремума модуля эмпирического процесса, называемого сейчас критерием Колмогорова. Затем Н.В.Смирнов исследовал супремум и инфимум эмпирического процесса, а также интеграл (по теоретической функции распределения) квадрата эмпирического процесса.

Следует отметить, что встречающееся иногда в литературе словосочетание "критерий Колмогорова-Смирнова", как подробно обосновано в статье, некорректно, поскольку эти два статистика никогда не печатались вместе и не изучали один и тот же критерий. Корректно сочетание "критерий типа Колмогорова-Смирнова", применяемое для обозначения критериев, основанных на использовании супремума функций от эмпирического процесса

После второй мировой войны развитие непараметрической статистики пошло быстрыми темпами. Большую роль сыграли работы Вилкоксона и его школы. К настоящему времени с помощью непараметрических методов можно решать практически тот же круг статистических задач, что и с помощью параметрических. Все большую роль играют непараметрические оценки плотности, непараметрические методы регрессии и распознавания образов (дискриминантного анализа). В нашей стране непараметрические методы получили достаточно большую известность после выхода в 1965 г. первого издания упомянутого выше сборника статистических таблиц Л. Н. Большева и Н. В. Смирнова, содержащего подробные таблицы для основных непараметрических критериев.

Тем не менее, параметрические методы всё еще популярнее непараметрических, особенно среди тех прикладников, кто слабо знаком со статистическими методами.

Неоднократно публиковались экспериментальные данные, свидетельствующие о том, что распределения реально наблюдаемых случайных величин, в частности, ошибок измерения, в подавляющем большинстве случаев отличны от нормальных (гауссовских). Тем не менее, теоретики продолжают строить и изучать статистические модели, основанные на гауссовости, а практики - применять подобные методы и модели.

Если в параметрических постановках на данных накладываются слишком жесткие требования - их функции распределения должны принадлежать определенному параметрическому семейству, то в непараметрических, наоборот, излишне слабые - требуется, лишь, чтобы функции распределения были непрерывны. При этом игнорируется априорная информация о том, каков "примерный вид" распределения. Априори можно ожидать, что учет этого "примерного вида" улучшит показатели качества статистических процедур. Развитием этой идеи является теория устойчивости (робастности) статистических процедур, в которой предполагается, что распределение исходных данных мало отличается от некоторого параметрического семейства. С 60-х годов эту теорию разрабатывали П. Хубер, Ф. Хампель и многие другие. Частными случаями реализации идеи робастности (устойчивости) статистических процедур являются рассматриваемые ниже статистика объектов нечисловой природы и интервальная статистика.

Имеется большое разнообразие моделей робастности в зависимости от того, какие именно отклонения от заданного параметрического семейства допускаются. Наиболее популярной оказалась модель выбросов, в которой исходная выборка "засоряется" малым числом "выбросов", имеющих принципиально иное распределение. Однако эта модель представляется "тупиковой", поскольку в большинстве случаев большие выбросы либо невозможны из-за ограниченности шкалы прибора, либо от них можно избавиться, применяя лишь статистики, построенные по центральной части вариационного ряда. Кроме того, в подобных моделях обычно считается известной частота засорения, что в сочетании со сказанным выше делает их малопригодными для практического использования.

Более перспективным представляется модель Ю. Н. Благовещенского, в которой расстояние между распределением каждого элемента выборки и базовым распределением не должно превосходить заданной малой величины.

Известно и другое из упомянутых выше направлений - бутстреп - связанное с интенсивным использованием возможностей вычислительной техники, что весьма актуально. Основная идея состоит в том, чтобы теоретическое исследование заменить вычислительным экспериментом по методу Монте Карло. Вместо описания выборки распределением из параметрического семейства строим большое число "похожих" выборок, т.е. "размножаем" выборку. Затем вместо оценивания характеристик и параметров и проверки гипотез на основе свойств теоретического распределения решаем эти задачи вычислительным методом, рассчитывая интересующие нас статистики по каждой из "похожих" выборок и анализируя полученные при этом распределения. Например, вместо того, чтобы теоретическим путем находить распределение статистики, доверительные интервалы и другие характеристики, моделируют много выборок, похожих на исходную, рассчитывают соответствующие значения интересующей исследователя статистики и изучают их эмпирическое распределение. Квантили этого распределения задают доверительные интервалы, и т.д.

Термин "бутстреп" мгновенно получил известность после первой же статьи Б. Эфрона 1979 г. по этой тематике. Он сразу же стал обсуждаться в массе публикаций, в том числе и научно-популярных. В "Заводской лаборатории" была помещена подборка статей по бутстрепу, выпущен сборник статей Б.Эфрона. Основная идея бутстрепа по Б.Эфрону состоит в том, что методом Монте-Карло (статистических испытаний) многократно извлекаются выборки из эмпирического распределения. Эти выборки, естественно, являются вариантами исходной, напоминают ее.

Сама по себе идея "размножения выборок" была известна гораздо раньше. Статья Б.Эфрона называется так: "Бутстреп-методы: новый взгляд на метод складного ножа". Упомянутый "метод складного ножа" (jackknife) предложен М. Кенуем еще в 1949 г., за 30 лет до статьи Б.Эфрона. "Размножение выборок" при этом осуществляется путем исключения одного наблюдения. При этом для выборки объема n получаем n "похожих" на нее выборок объема (n - 1) каждая. Если же исключать по 2 наблюдения, то число "похожих" выборок возрастает до n (n - 1) / 2 объема (n - 2) каждая.

Необходимо подчеркнуть, что бутстреп по Эфрону - лишь один из вариантов методов "размножения выборки" (resampling), и, на наш взгляд, не самый удачный. Метод "складного ножа" представляется более полезным. На его основе можно сформулировать следующую простую практическую рекомендацию.

Предположим, что Вы по выборке делаете какие-либо статистические выводы. Вы хотите узнать также, насколько эти выводы устойчивы. Если у Вас есть другие (контрольные) выборки, описывающие то же явление, то Вы можете применить к ним ту же статистическую процедуру и сравнить результаты. А если таких выборок нет? Тогда Вы можете их построить искусственно. Берете исходную выборку и исключаете один элемент. Получаете похожую выборку. Затем возвращаете этот элемент и исключаете другой. Получаете вторую похожую выборку. Поступив так со всеми элементами исходной выборки, получаете столько выборок, похожих на исходную, каков ее объем. Остается обработать их тем же способом, что и исходную, и изучить устойчивость получаемых выводов - разброс оценок параметров, частоты принятия или отклонения гипотез и так далее.

Можно изменять не выборку, а сами данные. Поскольку всегда имеются погрешности измерения, то реальные данные - это не числа, а интервалы (результат измерения плюс-минус погрешность). Нужна статистическая теория анализа таких данных.

Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы. Это направление математики является дальнейшим развитием всем известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции. К настоящему времени удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов.

Рассмотрим другое направление в статистике интервальных данных, которое также представляется перспективным. В нем развиваются асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, с помощью такой асимптотики были сформулированы правила выбора метода оценивания параметров гамма-распределения.

В развитие идей, в разработана общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания).

Она применена к оцениванию математического ожидания, дисперсии, коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в том числе с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова. Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на введенный нами показатель качества классификации. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих - оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных.

Согласно классификации статистических методов, принятой в, прикладная статистика делится на следующие четыре области:

статистика (числовых) случайных величин,

многомерный статистический анализ,

статистика временных рядов и случайных процессов,

статистика объектов нечисловой природы.

Первые три из этих областей являются классическими. Остановимся на четвертой. Ее именуют также статистикой нечисловых данных или попросту нечисловой статистикой.

Исходный объект в математической статистике - это выборка. В вероятностной теории статистики выборка - это совокупность независимых одинаково распределенных случайных элементов. Какова природа этих элементов? В классической математической статистике (той, что обычно преподают студентам) элементы выборки - это числа. В многомерном статистическом анализе - вектора. А в нечисловой статистике элементы выборки - это объекты нечисловой природы, которые нельзя складывать и умножать на числа. Другими словами, объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры.

Примерами объектов нечисловой природы являются:

значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций);

упорядочения (ранжировки) экспертами образцов продукции (при оценке ее технического уровня и конкурентоспособности)) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов);

классификации, т.е. разбиения объектов на группы сходных между собой (кластеры);

толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходства тематики научных работ, оцениваемого экспертами с целью рационального формирования экспертных советов внутри определенной области науки;

результаты парных сравнений или контроля качества продукции по альтернативному признаку ("годен" - "брак"), т.е. последовательности из 0 и 1;

множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга;

слова, предложения, тексты;

вектора, координаты которых - совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности (форма No.1-наука) или заполненная компьютеризированная история болезни, в которой часть признаков носит качественный характер, а часть - количественный;

ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты; и т.д.

Интервальные данные тоже можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств.

С начала 70-х годов под влиянием запросов прикладных исследований в технических, медицинских и социально-экономических науках в России активно развивается статистика объектов нечисловой природы, известная также как статистика нечисловых данных или нечисловая статистика. В создании этой сравнительно новой области прикладной математической статистики приоритет принадлежит российским ученым.

В течение 70-х годов на основе запросов теории экспертных оценок (а также социологии, экономики, техники и медицины) развивались конкретные направления статистики объектов нечисловой природы. Были установлены связи между конкретными видами таких объектов, разработаны для них вероятностные модели.

Следующий этап - выделение статистики объектов нечисловой природы в качестве самостоятельного направления в прикладной статистике, ядром которого являются методы статистического анализа данных произвольной природы. Программа развития этого нового научного направления впервые была сформулирована в статье. Реализация этой программы была осуществлена в 80-е годы. Для работ этого периода характерна сосредоточенность на внутренних проблемах нечисловой статистики.

К 90-м годам статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита, основные идеи, подходы и методы были разработаны и изучены математически, в частности, доказано достаточно много теорем. Однако она оставалась недостаточно апробированной на практике. Это было связано как с ее сравнительной молодостью, так и с общеизвестными особенностями организации науки в 80-е годы, когда отсутствовали достаточные стимулы к тому, чтобы теоретики занялись широким внедрением своих результатов. И в 90-е годы наступило время от математико-статистических исследований перейти к применению полученных результатов на практике.

Следует отметить, что в статистике объектов нечисловой природы, как и в других областях прикладной математической статистики и прикладной математики вообще, одна и та же математическая схема может с успехом применяться и в технических исследованиях, и в медицине, и в социологии, и для анализа экспертных оценок, а потому ее лучше всего формулировать и изучать в наиболее общем виде, для объектов произвольной природы.

В чем принципиальная новизна нечисловой статистики? Для классической математической статистики характерна операция сложения. При расчете выборочных характеристик распределения (выборочное среднее арифметическое, выборочная дисперсия и др.), в регрессионном анализе и других областях этой научной дисциплины постоянно используются суммы. Математический аппарат - законы больших чисел, Центральная предельная теорема и другие теоремы - нацелены на изучение сумм. В нечисловой же статистике нельзя использовать операцию сложения, поскольку элементы выборки лежат в пространствах, где нет операции сложения. Методы обработки нечисловых данных основаны на принципиально ином математическом аппарате - на применении различных расстояний в пространствах объектов нечисловой природы.

Кратко рассмотрим несколько идей, развиваемых в статистике объектов нечисловой природы для данных, лежащих в пространствах произвольного вида. Решаются классические задачи описания данных, оценивания, проверки гипотез - но для неклассических данных, а потому неклассическими методами.

Первой обсудим проблему определения средних величин. В рамках репрезентативной теории измерений удается указать вид средних величин, соответствующих тем или иным шкалам измерения. В классической математической статистике средние величины вводят с помощью операций сложения (выборочное среднее арифметическое, математическое ожидание) или упорядочения (выборочная и теоретическая медианы). В пространствах произвольной природы средние значения нельзя определить с помощью операций сложения или упорядочения. Теоретические и эмпирические средние приходится вводить как решения экстремальных задач. Для теоретического среднего это - задача минимизации математического ожидания (в классическом смысле) расстояния от случайного элемента со значениями в рассматриваемом пространстве до фиксированной точки этого пространства (минимизируется указанная функция от этой точки). Для эмпирического среднего математическое ожидание берется по эмпирическому распределению, то есть берется сумма расстояний от некоторой точки до элементов выборки и затем минимизируется по этой точке. При этом как эмпирическое, так и теоретическое средние как решения экстремальных задач могут быть не единственным элементом пространства, а состоять из множества таких элементов, которое может оказаться и пустым. Тем не менее удалось сформулировать и доказать законы больших чисел для средних величин, определенных указанным образом, то есть установить сходимость эмпирических средних к теоретическим.

Оказалось, что методы доказательства законов больших чисел допускают существенно более широкую область применения, чем та, для которой они были разработаны. А именно, удалось изучить асимптотику решений экстремальных статистических задач, к которым, как известно, сводится большинство постановок прикладной статистики. В частности, кроме законов больших чисел установлена и состоятельность оценок минимального контраста, в том числе оценок максимального правдоподобия и робастных оценок. К настоящему времени подобные оценки изучены также и в интервальной статистике.

В статистике в пространствах произвольной природы большую роль играют непараметрические оценки плотности, используемые, в частности, в различных алгоритмах регрессионного, дискриминантного, кластерного анализов. В нечисловой статистике предложен и изучен ряд типов непараметрических оценок плотности в пространствах произвольной природы, в частности, доказана их состоятельность, изучена скорость сходимости и установлен примечательный факт совпадения наилучшей скорости сходимости в произвольном случае с той, которая имеет быть в классической теории для числовых случайных величин.

Дискриминантный, кластерный, регрессионный анализы в пространствах произвольной природы основаны либо на параметрической теории - и тогда применяется подход, связанный с асимптотикой решения экстремальных статистических задач - либо на непараметрической теории - и тогда используются алгоритмы на основе непараметрических оценок плотности.

Для проверки гипотез могут быть использованы статистики интегрального типа, в частности, типа омега-квадрат. Любопытно, что предельная теория таких статистик, построенная первоначально в классической постановке, приобрела естественный (завершенный, изящный) вид именно для пространств произвольного вида, поскольку при этом удалось провести рассуждения, опираясь на базовые математические соотношения, а не на те частные (с общей точки зрения), что были связаны с конечномерным пространством.

Представляют интерес результаты, связанные с конкретными областями статистики объектов нечисловой природы, в частности, со статистикой нечетких множеств, со случайными множествами (следует отметить, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств, с непараметрической теорией парных сравнений, с аксиоматическим введением метрик в конкретных пространствах объектов нечисловой природы.

Для анализа нечисловых, в частности, экспертных данных весьма важны методы классификации. С другой стороны, наиболее естественно ставить и решать задачи классификации, основанные на использовании расстояний или показателей различия, в рамках статистики объектов нечисловой природы. Это касается как распознавания образов с учителем (другими словами, дискриминантного анализа), так и распознавания образов без учителя (то есть кластерного анализа). Современное состояние дискриминантного и кластерного анализа с точки зрения статистики объектов нечисловой природы отражено в ряде работ.

Статистические методы анализа нечисловых данных особенно хорошо приспособлены для применения в экономике, социологии и экспертных оценках, поскольку в этих областях от 50% до 90% данных являются нечисловыми.

В настоящее время признается необходимым изучение устойчивости (робастности) оценок параметров к малым отклонениям исходных данных и предпосылок модели. Однако популярная среди теоретиков (см. ниже в главе 10) модель засорения (Тьюки-Хьюбера) представляется не вполне адекватной. Эта модель нацелена на изучение влияния больших "выбросов". Поскольку любые реальные измерения лежат в некотором фиксированном диапазоне, а именно, заданном в техническом паспорте средства измерения, то зачастую выбросы не могут быть слишком большими. Поэтому представляются полезными иные, более общие схемы устойчивости, в частности, рассмотренные в главе 10 ниже, в которых, например, учитываются отклонения распределений результатов наблюдений от предположений модели.

Наиболее адекватной представляется новая эконометрическая модель, согласно которой результаты наблюдений - не числа, а интервалы. Например, если в таблице приведено значение 53,5, то это значит, что реальное значение - какое-то число от 53,0 до 54,0, т.е. какое-то число в интервале [53,5-0,5; 53,5+0,5], где 0,5 - максимально возможная погрешность. Принимая эту модель, мы попадаем в научную область под названием "статистика интервальных данных". Она идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы. Это направление математики является дальнейшим развитием всем известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции. По мнению ряда специалистов, статистика интервальных данных является частью интервальной математики. Впрочем, есть другая точка зрения, согласно которой такое включение нецелесообразно, поскольку статистика интервальных данных использует несколько иные подходы к алгоритмам анализа реальных данных, чем сложившиеся в интервальной математике (подробнее см. ниже).

Ниже развиваются асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, еще в начале 1980-х годов с помощью такой асимптотической теории были сформулированы правила выбора метода оценивания параметров гамма-распределения в ГОСТ 11.011-83.

Разработана общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания и дисперсии, медианы и коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих - оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных, найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия. Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на показатель качества классификации.

Как показала, в частности, международная конференция ИНТЕРВАЛ-92, в области асимптотической математической статистики интервальных данных российская научная школа имеет мировой приоритет. По нашему мнению, со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, "параллельные" обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.

Многие из утверждений статистики интервальных данных отличаются от аналогов из классической математической статистики. В частности, не существует состоятельных оценок; средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии оценки, рассчитанной согласно классической теории, и некоторого положительного числа (равного квадрату нотны - максимально возможного отклонения значения статистики из-за погрешностей исходных данных) - в результате метод моментов оказывается иногда точнее метода максимального правдоподобия; нецелесообразно увеличивать объем выборки сверх некоторого предела (называемого рациональным объемом выборки) - вопреки классической теории, согласно которой чем больше объем выборки, тем точнее выводы.

История развития статистики интервальных данных противоречива. Развитие идей статистики интервальных данных продолжается уже в течение 20 лет.

Одна из ведущих научных школ (как уже отмечалось выше) в области статистики интервальных данных - это школа проф. А.П. Вощинина, активно работающая с конца 70-х годов. Полученные результаты отражены в ряде монографий, статей, научных докладов, в том числе в трудах Международной конференции ИНТЕРВАЛ-92, диссертаций. В частности, изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности. Рассмотренное ниже направление исследований отличается нацеленностью на асимптотические результаты, полученные при больших объемах выборок и малых погрешностях измерений, поэтому оно и названо асимптотической статистикой интервальных данных.

Сформулируем сначала основные идеи асимптотической математической статистики интервальных данных, а затем рассмотрим реализацию этих идей на некоторых из перечисленных выше примеров. Следует сразу подчеркнуть, что основные идеи достаточно просты, в то время как их проработка в конкретных ситуациях зачастую оказывается достаточно трудоемкой.

Основные понятия асимптотической математической статистики интервальных данных.Пусть существо реального явления описывается выборкой x₁, x₂,..., x_n. В вероятностной теории математической статистики, из которой мы исходим (см. приложение 1 в конце книги), выборка - это набор независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка x₁, x₂,..., x_n, а величины

y_{j =} x_{j + j} , j = 1, 2,..., n, (282)

где j = 1, 2,..., n некоторые погрешности измерений, наблюдений, анализов, опытов, исследований (например, инструментальные ошибки).

Одна из причин появления погрешностей - запись результатов наблюдений с конечным числом значащих цифр. Дело в том, что для случайных величин с непрерывными функциями распределения событие, состоящее в попадании хотя бы одного элемента выборки в множество рациональных чисел, согласно правилам теории вероятностей имеет вероятность 0, а такими событиями в теории вероятностей принято пренебрегать. Поэтому при рассуждениях о выборках из нормального, логарифмически нормального, экспоненциального, равномерного, гамма - распределений, распределения Вейбулла-Гнеденко и др. приходится принимать, что эти распределения имеют элементы исходной выборки x₁, x₂,..., x_n, в то время как статистической обработке доступны лишь искаженные значения y_{j =} x_{j + j.}

Введем обозначения

x = (x₁, x₂,..., x_n), y = (y₁, y₂,..., y_n), ₍₂₈₃₎

Пусть статистические выводы основываются на статистике используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова: СТАТИСТИК ЗНАЕТ ТОЛЬКО f (y), НО НЕ f(x).

Очевидно, в статистических выводах необходимо отразить различие между f(y) и f(x). Одним из двух основных понятий статистики интервальных данных является понятие нотны.

Определение. Величину максимально возможного (по абсолютной величине) отклонения, вызванного погрешностями наблюдений , известного статистику значения f(y) от истинного значения f(x), то есть.

N_f(x) = sup | f(y) - f(x) |, (284)

где супремум берется по множеству возможных значений вектора погрешностей, будем называть НОТНОЙ.

Это означает, что исходные данные представляются статистику в виде интервалов (отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами - кроме абсолютных ошибок используются относительные или иные показатели различия между x и y.

Основные результаты в вероятностной модели. В классической вероятностной модели имеют элементы исходной выборки x₁, x₂,..., x_n рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа C > 0 такая, что в смысле сходимости по вероятности.

При использовании классических эконометрических методов в большинстве случаев используемая статистика f (x) является асимптотически нормальной.

В статистике интервальных данных ситуация совсем иная.

Основной проблемой, связанной с оцениванием параметров интервальной линейной статистической зависимости, является проблема отыскания решения интервальной системы линейных алгебраических уравнений (ИСЛАУ). G Z = S8, (1.3) где $$ - интервальная вещественная матрица размерности (пхт)9 Ш — п-мерный интервальный вектор, элементами которых являются соответственно интервалы \аша \ и [b 9b ]9 zeRm. Множество решений системы (13) может быть определено различными способами в зависимости от того, какими кванторами связаны коэффициенты матрицы, и вектора в правой части уравнения. Наиболее часто в литературе рассматриваются следующие множества решений ИСЛАУ: Ri={zeRm\ ЗСє $ґ ЗсєШ Cz = c} 2 = {zeR "\ V С є &f ЗсєШ Cz c) % {zeRm\ УсеШ ЗСє&ІЇ Cz = c] (1.4) Л,= {z єR " J (VCeQ/ Зеє Cz-c)& (VrfeSB 3 єс Z z = rf)}

Множества решений,,., / = 1,4 могут принимать различные эквивалентные формы и представления, широко описанные в литературе:

%t = {aeIT\ ([Х-,Х+] а) П [у-,у ] Щ (2={аєіГ [Х-,Х+] ас [у-,у+]} аи - {аєЛ" [ГД э [у-,/]} (285)

Здесь X" = Х+ = - матрицы нижних и верхних границ истинных значений независимых переменных размерностью (пхт), а у - (у 9,,.? у) г, у ={у%..9у1)Т - вектора нижних и верхних границ истинных значений зависимой переменной соответственно. Очевидны следующие отношения между множествами решений., / = 1,4 [62]: (Ьб)

Решение задачи оценивания параметров линейной регрессии с учетом присутствия интервальности в исходных данных и в предположении, что между зависимой переменной у и независимыми переменными хп і-\,т существует линейная связь, заключается в построении одного из приведенных множеств решений.

Существует множество постановок этой задачи и различные их решения. Так, формулируется задача построения множества решений при интервальном задании только значений выходных переменных, что объясняется присутствием ошибок измерения (абсолютных или относительных). Другими словами, рассматривается множество решений, совпадающее с, и 4 2, при следующих условиях: зависимость между выходной и независимыми переменными описывается линейно лараметризованой функцией, данные эксперимента описываются совокупностью п. опытов, независимые переменные заданы точечными значениями. Тогда в этом случае:

т Я]=Я2 = {аеКт\ у; хкі У; для всех к = \,п} (286)

В целях облегчения работы с множествами,,, %2, заданными в виде, предлагается способ их приближенного более простого описания прямоугольной гиперпризмой

П+т где: ІҐ ={ає/Г a; af a; i = ljn}9 І (287