Выберем теперь произвольный интервал 
, содержащийся внутри 
. Точкам этого интервала отвечают ординаты кривой, удовлетворяющие неравенству 
. Поэтому, если 
принадлежит интервалу , то
принадлежит интервалу 
, и наоборот. Значит: 
. Так как равномерно распределена в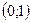 
, то
, а это как раз и означает, что случайная величина , являющаяся корнем уравнения и имеет плотность вероятностей 
.
Простейшим потоком (или потоком Пуассона) в СМО называется такой поток заявок, когда промежуток времени 
между двумя последовательными заявками есть случайная величина, распределенная на интервале 
с плотностью
(141)
Вычислим математическое ожидание: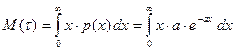 
(142)
После интегрирования по частям, получим:
. (143)
Параметр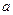 
есть интенсивность потока заявок.
Формулу для розыгрыша мы получим из уравнения, которое в данном случае запишется так: 
. (144)
Вычислив интеграл, стоящий слева, мы получим соотношение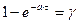 
. Отсюда, выражая , получим:
(145)
Так как величина 
распределена также как и , следовательно, формулу можно записать в виде:
(146)
Пусть исследуемое предприятие представляет собой двухканальную систему массового обслуживания с ограниченной очередью. На вход информации поступает пуассоновский поток заявок с интенсивностью λ. Интенсивности обслуживания заявок каждым из каналов μ, а максимальное число мест в очереди m.
Начальные параметры такие:
Время обслуживания заявок тогда имеет эмпирическое распределение, указанное ниже и имеет среднее значение 
.
Были проведены контрольные замеры времени обработки заявок, поступающих в данную СМО. Чтобы приступить к исследованию, необходимо установить по этим наблюдениям закон распределения времени обработки заявок.
Таблица 15. – Группировка заявок по времени обработки
| Количество заявок | ||||||||
| Время обработки, мин | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 | 25–30 | 30–35 | 35–40 |
Нами выдвигается гипотеза о показательном распределении генеральной совокупности.
Для того чтобы, при уровне значимости 
качественно проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:
1) Найти по заданному эмпирическому распределению выборочную среднюю 
. Для этого, каждый i – й интервал заменяем его серединой 
и составляем последовательность равноотстоящих вариант и соответствующих им частот.
2) Принять в качестве оценки параметра λ показательного распределения величину, которая обратна выборочной средней:
(148)
3) Найти нужные вероятности попадания X в частичные интервалы по формуле:
(149)
4) Потом вычислить теоретические частоты:
, (150)
где 
- объем выборки
5) Сравнить эмпирические и теоретические частоты можно с помощью критерия Пирсона, приняв число степеней свободы 
, где S – число интервалов первоначальной выборки.
Таблица 16. – Показывает группировку заявок по времени обработки с усредненным временным интервалом
| Количество заявок | ||||||||
| Время обработки, мин | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 | 32,5 | 37,5 |
Н
Теперь найдем выборочную среднюю:
Рисунок 104.
2) Примем в качестве оценки параметра λ экспоненциального распределения величину, равную 
. Тогда получим:
(
) (151)
3) Теперь найдем вероятности попадания X в каждый из интервалов по формуле:
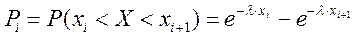(152)
Для первого интервала:
(153)
Для второго интервала:
(154)
Для третьего интервала:
(155)
Для четвертого интервала:
(156)
Для пятого интервала:
(157)
Для шестого интервала:
(158)
Для седьмого интервала:
(159)
Для восьмого интервала:
(160)
4) Вычислим теоретические частоты:
(161)
Эти результаты вычислений заносим в таблицу. Сравниваем эмпирические 
и теоретические 
частоты с помощью критерия Пирсона.
Для этого надо вычислить разности 
, их квадраты, затем отношения 
. (162)
Суммируя значения последнего столбца, находим нужное нам наблюдаемое значение критерия Пирсона. По таблице критических точек распределения 
при уровне значимости 
и числу степеней свободы 
находим эту критическую точку 
Таблица 17. – Результаты вычислений следующие:
| i |
| 
| 
|
| 
|
|
| 0,285 | 34,77 | -12,77 | 163,073 | 4,690 | ||
| 0,204 | 24,888 | 0,112 | 0,013 | 0,001 | ||
| 0,146 | 17,812 | 5,188 | 26,915 | 1,511 | ||
| 0,104 | 12,688 | 3,312 | 10,969 | 0,865 | ||
| 0,075 | 9,15 | 4,85 | 23,523 | 2,571 | ||
| 0,053 | 6,466 | 3,534 | 12,489 | 1,932 | ||
| 0,038 | 4,636 | 3,364 | 11,316 | 2,441 | ||
| 0,027 | 3,294 | 0,706 | 0,498 | 0,151 | ||
|
Так как 
, то у нас нет оснований отвергнуть гипотезу о распределении X по показательному закону. Другими словами, данные наблюдений вполне согласуются с этой гипотезой.
Очевидно, что данная система представляет собой частный случай системы гибели и размножения.
Граф данной системы:
Рисунок 105. – граф состояний исследуемой СМО
Поскольку все состояния являются сообщающимися и существенными, то определенно существует предельное распределение вероятностей состояний. Как мы знаем стационарных условиях поток, входящий в данное состояние должен быть равен потоку, выходящему из данного состояния.
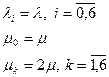(163)
Тогда для состояния S0:
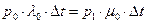(164)
Следовательно:
(165)
Тогда для состояния S1:
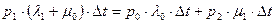(166)
Следовательно:
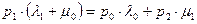(167)
С учетом того, что :
(168)
(169)
Аналогичным образом получаем уравнения для остальных состояний системы. В результате чего получим систему уравнений:
Рисунок 106.
Тогда решение этой системы будет иметь вид:
; 
; 
; 
; 
;
; 
.
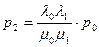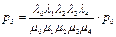Рисунок 107.
Или,
; 
; 
; 
; 
; 
;
.
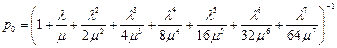
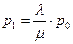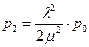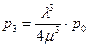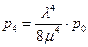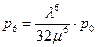Рисунок 108.
Тогда коэффициент загруженности СМО:
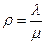
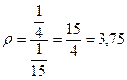
Рисунок 109.
С учетом этого предельные вероятности перепишем в виде:
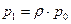
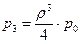
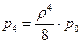
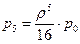
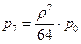
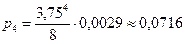
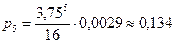
Рисунок 110.
Наиболее вероятные состояния – оба канала СМО заняты и также заняты все места в очереди.
Тогда вероятность образования очереди:
(170)
Отказ в обслуживании заявки происходит тогда, когда все m мест в очереди заняты, то есть:
(171)
Тогда относительная пропускная способность равна:
(172)
Отсюда вероятность того, что вновь поступившая заявка будет обслужена, равна 0,529
Следовательно, абсолютная пропускная способность:
(173)
СМО обслуживает в среднем 0,13225 заявок в минуту.
Тогда среднее число заявок, находящихся в очереди будет равно:
(174)
Среднее число заявок в очереди очень близко к максимальной длине очереди.
Среднее число заявок, обслуживаемых в нашем СМО, может быть записано в виде:
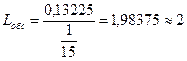(175)
Тогда очевидно, что в среднем все каналы СМО постоянно заняты.
А среднее число заявок, находящихся в СМО:
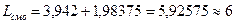(176)
Для открытых СМО будут справедливы формулы Литтла:
Тогда среднее время пребывания заявки с СМО:
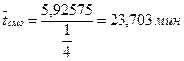(177)
А среднее время пребывания заявки в очереди:
(178)
Скорее всего, наиболее вероятное состояние данной СМО – занятость всех каналов и мест в очереди. Очевидно, что приблизительно половина всех поступающих заявок покидают СМО необслуженными. Приблизительно 66,5% времени ожидания падает на ожидание в очереди. Оба канала всегда заняты. Все это говорит о том, что данная схема СМО может быть признана полностью неудовлетворительной.
Чтобы понизить загрузку каналов, сократить время ожидания в очереди и снизить вероятность отказа необходимо увеличить число каналов и ввести систему приоритетов для заявок. Число каналов будет целесообразно увеличить примерно до 4. Также желательно сменить дисциплину обслуживания с FIFO на систему с приоритетами. Все заявки тогда будут иметь принадлежность к одному из двух приоритетных классов. Заявки I класса имеют относительный приоритет по отношению к заявкам II класса. Для расчета основных показателей такой видоизмененной СМО целесообразно применить какой-либо из методов имитационного моделирования.
Пользователю при работе с программой на компьютере необходимо задать основные параметры СМО, такие как интенсивности потоков, количество каналов, приоритетных классов, мест в очереди (если количество мест в очереди равно нулю, то СМО с отказами), а также временной интервал модуляции и количество испытаний. Программа преобразовывает сгенерированные случайные числа, таким образом, пользователь получает последовательность временных интервалов 
, распределенных показательно. После чего отбирается заявка с минимальным , и ставится в очередь, согласно ее приоритету. За то же время происходит перерасчет очереди и каналов. Затем эта операция будет повторяется до окончания времени модуляции, задаваемого изначально. В исзодном теле программы присутствуют счетчики, на основании показаний которых и формируются основные показатели СМО. Если для увеличения точности было задано несколько испытаний, тогда в качестве конечных результатов принимается оценка за серию опытов. Такие программы достаточно универсальны, с их помощью могут быть исследованы СМО с любым количеством приоритетных классов, либо вообще без приоритетов. Для проверки корректности работы алгоритма, в него водят такжк исходные данные классической СМО, изложенная выше. Программы моделируют результаты близкий к тому, который получаются с помощью методов теории массового обслуживания. Погрешность же возникающая в ходе имитационного моделирования, может быть объяснена тем, что проведено недостаточное количество испытаний. Результаты, полученные с помощью программ для СМО с двумя приоритетными классами и увеличенным числом каналов, показывают целесообразность этих изменений.
Высший приоритет присвавается более «быстрым» заявкам, что позволяет быстро обследовать короткие задания. Сокращается средняя длина очереди в системе, а соответственно минимизируется средство для организации очереди. В качестве основного недостатка данной организации можно выделить то, что «долгие» заявки находятся в очереди длительно время или вообще получают отказ. Введенные приоритеты могут быть переназначены после оценки полезности того или иного типа заявок для СМО.
2.8.1. Понятие и сущность сетевого планирования и управления.
Методы сетевого планирования и управления (СПУ), разработанные в начале 50-х годов, широко и успешно применяются для оптимизации планирования и управления сложными взаимосвязанными и разветвленными комплексами работ, требующими участия большого числа исполнителей и затрат ограниченных ресурсов.
Все началось в 1956 году, когда М. Уолкер из фирмы Дюпон, исследуя возможности использования более эффективного использования принадлежащей фирме вычислительной машины Univac, обьеденил свои усилия с Д. Келли из группы планирования капитального строительства. В результате был создан так называемый Метод Критического Пути – МКП (или CPM – Critical Path Method).
Параллельно и независимо от них в военно-морских силах США был создан метод анализа и оценки программ PERT (Program Evaluation and Review Technique). Этот метод был разработан корпорацией Локхид при планировании и управлении разработкой ракетной системы Поларис, которая объединяла около 3800 основных подрядчиков и 60000 операций. В результате применения этого метода все работы были закончены на два года раньше срока, а метод был засекречен на уровне военной тайны США.
Конечно в настоящее время для оптимизации сложных сетей, состоящих из нескольких сотен или тысяч работ, вместо ручного счета применяется типовые макеты прикладных программ по СПУ (сетевое планирование и управление), имеющиеся в составе программного и математического обеспечения вычислительной техники.
Основными и исходными понятиями сетевых моделей являются понятия - события и работы.
На графике отражаются «работы» и «события». Каждое событие отражает т завершение или начало работы, а работа означает действие, которое нужно совершить, чтобы перейти от предшествующего события к последующему. События на графике обозначаются кружками, а работы — стрелками, показывающими связь между событиями (возможен, но редко и другой вариант: работы изображаются кружками, а связи между ними стрелками). Работа должна быть конкретно определена, четко описана и иметь ответственного исполнителя, продолжительность её измеряется количеством времени, а также работа связана с использованием ресурсов. Временные оценки даются экспертами или ответственными исполнителями соответствующих работ. Все работы в графике ведут к конечному событию — цели планирования откуда не выходит никаких работ.
Таким образом - работа - это некоторый процесс, приводящий к достижению опреде-ленного результата и требующий затрат каких-либо ресурсов, и имеет протяженность во времени.
По своей физической природе любые работы можно рассматривать как:
- действие: например - изготовление деталей, заливка фундамента, составление заявки на материалы, наблюдение и изучение конъюнктуры рынка и т.д.;
- процесс: например - старение отливок, выдерживание вина в бочках, травление плат и т.д.;
- ожидание: например - ожидание поставки комплектующих, прослеживание детали в очереди к станку, ожидание результатов проверок и тому подобное.
По количеству затрачиваемого времени работа, делится на:
- действительную, т.е. требующей затрат времени;
- фиктивную, не требующей затрат времени и представляющей связь
между какими-либо работами и технологически необходимой: например - передача измененных чертежей от конструкторов к технологам, детали с одного рабочего места на другое, сдача отчета в налоговую инспекцию или отчета о технико-экономических показателях работы цеха вышестоящему подразделению.
Событие - момент времени, когда полностью завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и в отличие от работ не имеет протяженности во времени. Например, фундамент залит бетоном, старение отливок завершено, комплектующие поставлены, отчеты сданы и так далее.
Заданный комплекс работ упорядочивается в их логической последовательности с выделением различных групп работ, которые могут и должны выполняться параллельно. Для таких групп работ могут составляться частные сетевые графики, которые затем обьединяются в единый сводный сетевой график. В целях уменьшения общего времени для каждой работы проверяется возможность переноса ее начала ближе к исходному, а конца ближе к завершающему событиям сетевого графика и при наличии такой возможности перестроить сетевой график.
Таким образом, начало, и окончание любой работы отражаются парой событий, которые называются начальным и конечнымсобытиями. Поэтому для идентификации конкретной работы используют код работы (i,j), состоящий из номеров начального (i-ro) и конечного (j-го) событий, например (2,4) или 3 – 8 или 9, 10 или работа i,j
На этапе структурного планирования взаимосвязь работ и событий
изображаются с помощью сетевого графика, где работы изображаются
стрелками, которые соединяют вершины, изображающие события. Работы,
выходящие из некоторого события не могут начаться, пока не будут завершены абсолютно все операции, входящие в это событие.
Рисунок 111.
Событие, не имеющее предшествующих ему событий, то есть с которого начинается проект, называют исходнымсобытием или истоком сетевой модели. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающимили стоком сети.
Рисунок 112.
Итак при построении сетевого графика необходимо следовать следующим правилам:
■ длина стрелки никак не зависит от времени выполнения работы;
Рисунок 113
|
§ стрелка совсем не обязательно должна представлять прямолинейный отрезок;
Рисунок 114.
|
■ для действительных работ обычно используются сплошные, а для фиктивных пунктирные стрелки;
Рисунок 115.
§ каждая операция должна быть представлена обязательно только одной стрелкой;
§ категорически не должно быть параллельных работ между одними и теми же событиями, для избежания такой ситуации используют фиктивные работы;
