Если система S может переходить в другое состояние случайным образом в произвольный момент времени, то тогда говорят о случайном процессе с непрерывным временем. В отсутствии последствия такой процесс называется непрерывной марковской цепью. При этом вероятности переходов 
для любых i и j в любой момент времени равны нулю (в силу непрерывности времени). По этой причине вместо вероятности перехода 
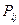вводится величина 
- плотность вероятности перехода из состояния 
в состояние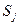 
, определяемая как предел:
(116)
Если эти величины 
не зависят от t, то марковский процесс называется однородным. Если за время 
система может изменить свое состояние не более чем один раз, то говорят, что случайный процесс является ординарным. Величину принято называть интенсивностью перехода системы из Si в Sj. На графе состояний системы численные значения всегда ставят рядом со стрелками, показывающими переходы в вершины графа.
Зная интенсивности переходов можно найти величины p1(t), p2(t),…, pn(t) – вероятности нахождения системы S в состояниях S1, S2,…, Sn соответственно. При этом выполняется условие:
(117)
Распределение таких вероятностей состояний системы, которое можно характеризовать вектором 
, называется стационарным, если оно не зависит от времени, то есть все компоненты вектора 
являются константами.
В свою очередь состояния Si и Sj называются сообщающимися, если возможны переходы 
.
Если состояние Si называется существенным, если всякое Sj, достижимое из Si, является сообщающимся с Si. Тогда состояние Si называется несущественным, если оно не является существенным.
Если существуют предельные вероятности состояний системы то:
, (118)
не зависящие от начального состояния системы, тогда говорят, что при 
в системе устанавливается стационарный режим.
Система, в которой существуют предельные (финальные), вероятности состояний системы, называется эргодической, и соответственно протекающий в ней случайный процесс эргодическим.
Теорема 1. Если Si – несущественное состояние, то 
то есть при система выходит из любого несущественного состояния.
Теорема 2. Чтобы система с конечным числом состояний имела единственное предельное распределение вероятностей состояний, необходимо и достаточно, чтобы все ее существенные состояния сообщались между собой.
Если случайный процесс, происходящий в системе с дискретными состояниями является непрерывной марковской цепью, то для вероятностей p1(t), р2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. При составлении уравнений удобно пользоваться графом состояний системы. В левой части каждого из них стоит производная вероятности какого-то (j-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых возможен переход в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.
