Процесс отыскания возможных значений случайной величины Х (собственно моделирование) называют «разыгрыванием случайной величины».
Метод Монте-Карло дает возможность моделировать абсолютно любой процесс, на протекание которого влияют случайные факторы. Для многих экономико математических задач, не связанных с какими-либо случайностями, можно искусственно смоделировать вероятностную модель, которая в некоторых случаях является более выгодной.
В отличие от аналитических методов, ищущих решение в виде ряда по конкретным собственным функциям, методы Монте-Карло как правило ищут решения в виде статистических сумм. Для их применения вполне достаточно описания самого вероятностного процесса и не обязательна его формулировка в виде интегрального уравнения; оценка погрешности чрезвычайно проста, их точность слабо зависит от размерности пространства.
Главный же недостаток метода Монте-Карло заключается в том, что, являясь в основном численным методом, он не может заменить аналитические методы при расчете существенно новых явлений, где, нет статистики и прежде всего, нужно раскрытие качественных закономерностей.
Главное же преимущество метода Монте-Карло состоит в том, что он способен “сработать” там, где отказывают все другие методы.
Аналитические же методы исследования позволяют существенно уменьшить возможные погрешности метода Монте-Карло и могут поднять его до уровня получения качественных закономерностей. Синтез таких аналитических и статистических методов позволяет свести D к очень малой величине, и, следовательно, уменьшить погрешность.
Приведем примеры некоторых задач, успешно решаемых методом Монте-Карло:
– расчет системы массового обслуживания;
– расчет качества и надежности изделий;
– теория передачи сообщений;
– вычисление определенного интеграла;
– задачи вычислительной математики;
– задачи нейтронной физики и другие.
Имитационное моделирование по методу Монте-Карло (Monte-Carlo Simulation) позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию) получить распределение доходности проекта.
Блок-схема, представленная на рисунке отражает укрупненную схему работы с моделью.
Рисунок. 102.
Конечно, применение метода имитации Монте-Карло требует использования специальных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master), в то время как метод сценариев может быть реализован даже при помощи средств MS Office и даже обыкновенного калькулятора.
Как уже отмечалось, анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой соединение методов анализа чувствительности и анализа сценариев на базе теории вероятностей.
Результатом такого комплексного анализа выступает распределение вероятностей всех возможных результатов проекта (например, вероятность получения NPV<0).
Программный пакет Risk-Master позволяет в диалоговом режиме осуществить процедуру подготовки информации к анализу рисков инвестиционного проекта по методу Монте-Карло и провести сами необходимые расчеты.
Первый шаг при применении метода имитации состоит в определении функции распределения каждой переменной, которая может оказывать влияние на формирование потока. Как правило, предполагается, что функция распределения являются нормальной, и, следовательно, для того, чтобы задать ее необходимо определить всего два показателя (математическое ожидание и дисперсию).
Как только функция распределения будет определена, можно применять процедуру Монте-Карло.
Шаг 1.Опираясь на использование статистического пакета, случайным образом выбираем, основываясь на вероятностной функции распределения значение переменной, которая является одним из параметров определения потока наличности.
Шаг 2. Выбранное значение случайной величины наряду со значениями переменных, которые являются экзогенными переменными, используется при подсчете чистой приведенной стоимости проекта.
Шаги 1 и 2 повторяются необходимое количество раз, например 1000 (можно и меньше если распределение будет близким к нормальному), и полученные 1000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.
Используя значения математического ожидания и стандартного отклонения, можно легко вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта, как и в анализе, методом сценариев.
Теперь необходимо определить минимальное и максимальное значения критической переменной, а для переменной с пошаговым распределением помимо этих двух еще и остальные значения, принимаемые ею. Границы варьирования переменной определяются, очень просто исходя из всего спектра возможных значений.
По прошлым наблюдениям за переменной можно установить также и частоту, с которой та принимает соответствующие значения. В этом случае вероятностное распределение есть то же самое частотное распределение, которое показывает частоту встречаемости значения, правда, в относительном масштабе (от 0 до 1). Вероятностное распределение регулирует вероятность выбора значений из конкретного определенного интервала. В соответствии с этим заданным распределением модель оценки рисков будет выбирать произвольные значения переменной. До рассмотрения рисков подразумевается, что переменная принимает одно определенное нами значение с вероятностью 1. И через одну единственную итерацию расчетов мы получали однозначно определенный результат. В рамках модели вероятностного анализа рисков необходимо проводить большое число итераций, позволяющих установить, как ведет себя результативный показатель (в каких пределах колеблется, как распределен) при подстановке в модель различных значений переменной в соответствии с заданным распределением.
Задача аналитика, занимающегося таким анализом риска, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной (фактора) вид вероятностного распределения. При этом основные вероятностные распределения, используемые в анализе рисков, могут быть, в основном следующими: нормальное, постоянное, треугольное, пошаговое. Эксперт присваивает переменной какое то вероятностное распределение, исходя из своих количественных ожиданий и делает выбор из двух категорий распределений: симметричных (например, нормальное, постоянное, треугольное) и несимметричных (например, пошаговое распределение).
Существование коррелированных переменных (мультиколлениарность) в проектном анализе вызывает порой проблему, не рассмотреть которую означало бы заранее обречь себя на неверные результаты. Ведь без учета коррелированности, скажем, двух переменных - компьютер, посчитав их полностью независимыми, генерирует совершенно нереалистичные проектные сценарии. Допустим цена, и количество проданного продукта есть две отрицательно коррелированные переменные (не всегда, но как правило). Если не будет уточнена связь между переменными (коэффициент корреляции), то возможны сценарии, случайно вырабатываемые компьютером, где цена и количество проданной продукции будут всегда вместе, либо высокими, либо низкими, что естественно негативно отразится на результате.
Проведение расчетных итераций является полностью компьютеризирован-ная часть анализа рисков проекта. 200-500 итераций обычно достаточно для хорошей репрезентативной выборки (с учетом достаточно четкого распределения). В процессе каждой итерации всегда происходит случайный выбор значений ключевых переменных из специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например, NPV). И так далее, от итерации к итерации.
Завершающая стадия анализа проектных рисков это интерпретация результатов, собранных в процессе итерационных расчетов. Результаты анализа рисков можно представить, например в виде профиля риска. На нем должна графически показываться вероятность каждого возможного случая (имеются в виду вероятности возможных значений результативного показателя).
Часто при сравнении, например вариантов капиталовложений удобнее пользоваться кривой, построенной на основе суммы вероятностей (кумулятивный профиль риска). Такая кривая показывает вероятности того, что результативный показатель проекта может быть больше или меньше определенного значения. Проектный риск, таким образом, описывается положением и наклоном кумулятивного (накопленного) профиля риска.
Кумулятивный (интегральный, накопленный) профиль риска, показывает кумулятивное вероятностное распределение чистой текущей стоимости (NPV) с разных точек зрения - банкира, предпринимателя и экономиста на определенный проект. Вероятность того, что NPV < 0 с точки зрения экономиста - около 0.4, а в то время как для предпринимателя эта вероятность менее 0.2. С точки зрения банкира проект может казаться совсем безопасным, так как вероятность того, что NPV > 0, около 95%.
Будем исходить из того, что проект может подлежать рассмотрению и считается выгодным, в случае, если NPV > 0. При сравнении нескольких одноцелевых проектов выбирается тот, у которого NPV больше при соблюдении сказанного выше.
Рассмотрим пять иллюстративных случаев на рисунке принятия решений. Случаи 1-3 имеют дело с решением инвестировать в один отдельно взятый проект, тогда как два последних случая (4, 5) относятся к необходимостью решения-выбора из альтернативных проектов. В каждом случае рассматривается как кумулятивный (накопленный), так и некумулятивный профили риска для сравнительных целей. Кумулятивный профиль риска будет более полезен в случае выбора наилучшего проекта из представленных альтернатив, в то время как некумулятивный профиль риска лучше индуцирует вид распределения и показателен для понимания всех концепций, связанных с определением математического ожидания. Обычно анализ базируется на показателе чистой текущей стоимости.
Случай 1: Минимальное возможное значение NPV выше, чем нулевое (см. Рис.103, кривая 1).
Рисунок 103.
Вероятность отрицательного NPV равна 0, так как нижний конец кумулятивного профиля риска лежит справа от нулевого значения NPV. Так как данный проект имеет положительное значение NPV во всех случаях, ясно, что проект будет принят.
Случай 2: Если максимальное возможное значение NPV ниже нулевого (кривая 2).
Вероятность положительного NPV равна 0 (см. следующий рисунок), так как верхний конец кумулятивного профиля риска лежит слева от нулевого значения NPV. Так как данный проект имеет отрицательное значение NPV во всех случаях, ясно, что проект не может быть принят.
Случай 3: В случае если максимальное значение NPV больше, а минимальное меньше нулевого (кривая 3).
Вероятность нулевого NPV больше, чем 0, но при этом меньше, чем 1, так как вертикаль нулевого NPV пересекает кумулятивный профиль рисков. Так как NPV может быть как отрицательным, так и положительным, то решение будет зависеть от предрасположенности к риску инвестора. Видимо, если математическое ожидание NPV меньше или равно 0 (пик профиля рисков слева от вертикали или вертикаль точно проходит по пику) проект должен отклоняться от дальнейшего рассмотрения.
Случай 4: Здесь видим непересекающиеся кумулятивные профили рисков альтернативных (взаимоисключающих) проектов (см. Рис.104).
Рисунок. 104.
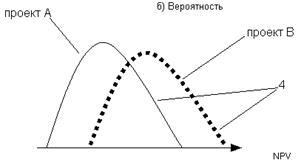
Очевидно, что при фиксированной вероятности отдача проекта В всегда выше, нежели у проекта А. Профиль рисков также может говорить о том, что при фиксированной NPV вероятность, с которой та будет достигнута, начиная с некоторого уровня, будет выше для проекта, В, чем для проекта А., Таким образом, мы и подошли к правилу 1.
Правило 1: Если кумулятивные профили рисков двух альтернативных проектов никогода не пересекаются ни в одной точке, тогда следует выбирать тот проект, чей профиль рисков расположен правее.
Случай 5: Наблюдаем пересекающиеся кумулятивные профили рисков альтернативных проектов. (См. Рис.105).
Рисунок. 105
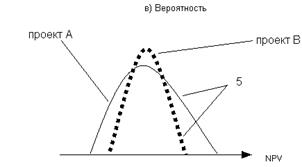
Склонные к риску инвесторы, как правило, предпочтут возможность получения высокой прибыли и, таким образом, выберут проект А. Не склонные к риску инвесторы напротив предпочтут возможность нести низкие потери и, вероятно, выберут проект В.
Правило 2: Если кумулятивные профили риска альтернативных проектов пересекаются в какой-либо точке, то тогда решение об инвестировании зависит от склонности к риску инвестора.
Ожидаемая стоимость всегда агрегирует информацию, содержащуюся в вероятностном распределении. Она получается в результате умножения каждого значения результативного показателя на соответствующую вероятность и последующего суммирования результатов. Сумма же всех отрицательных значений показателя, перемноженных на соответствующие вероятности и есть ожидаемый убыток. Ожидаемый выигрыш это сумма всех положительных значений показателя, перемноженных на соответствующие вероятности. И наконец ожидаемая стоимость есть, конечно, их сумма.
Надо заметить, что в качестве индикатора риска ожидаемая стоимость может выступать как надежная оценка только в ситуациях, где операция, связанная с данным риском, может быть повторена много раз. Хорошим примером такого риска служит риск, страхуемый страховыми компаниями, когда они предлагают одинаковые контракты большому числу клиентов. В инвестиционном проектировании мера ожидаемой стоимости должна всегда применяться в комбинации с какой-то мерой вариации, такой как стандартное отклонение.
Инвестиционное решение не должно базироваться только лишь на одном значении ожидаемой стоимости, потому что индивид не может быть равнодушен к различным комбинациям значения показателя отдачи и соответствующей вероятности, из которых складывается ожидаемая стоимость.
Издержки неопределенности или истинная ценность информации, как они иногда называются, - полезное понятие, помогающее определить максимально возможную плату за получение информации, сокращающей неопределенность проекта. Эти издержки можно определить, как ожидаемую стоимость возможного выигрыша при решении отклонить проект или наоборот как ожидаемую стоимость возможного убытка при решении принять проект.
Ожидаемая стоимость возможного выигрыша при решении отклонить проект иллюстрируется на Рис.106 и равна сумме возможных положительных значений NPV, перемноженных на соответствующие вероятности.
Рисунок. 106.
Ожидаемая стоимость возможного убытка при решении принять проект, показанна в виде заштрихованной площади на Рис.107, и равна сумме возможных отрицательных значений NPV, перемноженных на соответствующие вероятности.
Рисунок. 107.
В результате оценив возможное сокращение издержек неопределенности при приобретении дополнительной информации, инвестор решает, отложить решение принять или отклонить проект и искать дополнительную информацию или принимать решение немедленно. Общее правило здесь таково: инвестору следует отложить решение, если возможное сокращение в издержках неопределенности превосходит издержки получения дополнительной информации.
Нормированный ожидаемый убыток (НОУ) это отношение ожидаемого убытка к ожидаемой стоимости:
НОУ = ожидаемый убыток/(ожидаемый выигрыш + ожидаемый убыток)
Этот показатель может принимать значения от 0 (то есть отсутствие ожидаемого убытка) до 1 (то есть отсутствие ожидаемого выигрыша). На Рис.107 он представляется как отношение площади под профилем риска слева от нулевого NPV - ко всей площади под профилем риска
Проект с таким вероятностным распределением NPV, таким, что область определения профиля риска NPV выше 0, имеет нормируемый ожидаемый убыток, равный 0, что означает абсолютную неподверженность риску проекта. А с другой стороны, проект, область определения профиля риска NPV которого ниже 0, полностью подвержен риску.
Этот показатель определяет риск как следствие двух вещей: наклона и положения профиля риска NPV по отношению к разделяющей вертикали нулевого NPV.
Он представляет из себя стандартное отклонение результативного показателя, деленное на его ожидаемую стоимость. При положительной ожидаемой стоимости, чем ниже такой коэффициент вариации, тем меньше проектный риск.
Как видим, два последних из рассмотренных показателей характеризуют риск исследуемого проекта. Однако понятно, что если нормируемый ожидаемый убыток есть относительный показатель и дает возможность судить о риске отдельно взятого проекта (скажем, неудовлетворительным считается проект, НОУ которого более 40%), то коэффициент вариации это абсолютный показатель, и потому представляется более удобным для его использования при сравнении альтернативных проектов.
Степень устойчивости проекта по отношению ко всем возможным изменениям условий реализации, а значит, и степень риска может быть охарактеризована показателями предельного уровня объемов производства, цен производимой продукции и других параметров проекта. Предельное значение параметра проекта для некоторого t-го года его реализации определяется как такое значение этого параметра в t-ом году, при котором чистая прибыль участника в этом году станет нулевой. Одним из наиболее важных показателей этого типа является рассмотренная нами ранее точка безубыточности, характеризующая объем продаж, при котором выручка от реализации продукции полностью совпадает с издержками производства.
Для подтверждения работоспособности такого проектируемого производства (на данном шаге расчета) необходимо, чтобы значение точки безубыточности было меньше значений номинальных объемов производства и продаж (на этом шаге). Чем дальше от них значение такой точки безубыточности (в процентном отношении), тем устойчивее проект. Проект обычно признается всеми устойчивым, если значение такой точки безубыточности не превышает 75% от номинального объема производства. Подробно данный показатель, а также его плюсы и минусы уже рассматривались нами ранее.
Как мы видим, данный показатель никак не связан с вероятностным методом и в отличие от последнего никак не уточняет вероятности и спектр возможных значений для результативных показателей. Кроме того, каждый показатель предельного уровня характеризует степень устойчивости в зависимости лишь от конкретного параметра проекта (объем производства, например, и так далее), в то время как вероятностный подход проводит комплексный анализ риска при неопределенности одновременно всех интересующих нас параметров проекта, то есть в последнем случае учитывается синхронность их изменения.
На практике не имеет никакого смысла считать большое количество показателей предельного уровня с надеждой определить риски, так как основная цель расчета такого, несомненно, важного показателя как точка безубыточности состоит в том, чтобы определить минимально допустимый уровень объема производства на прединвестиционной фазе, что необходимо при описании проекта и построении его основной идеи.
Несмотря на все свои достоинства, метод Монте-Карло не распространен и не используется слишком широко в экономике. Одна из главных причин этого - неопределенность функций плотности переменных, которые используются при подсчете потоков наличности она не вполне понятна экономистам.
Другая проблема, которая возникает как при использовании метода сценариев, так и при использовании метода Монте-Карло, состоит в том, что применение обоих методов не дает однозначного ответа на вопрос о том, следует ли реализовывать данный проект или следует отвергнуть его, что не устраивает математиков.
При завершении анализа, проведенного методом Монте-Карло, у эксперта всегда есть значение ожидаемой чистой приведенной стоимости проекта и плотность распределения этой случайной величины. Однако наличие этих данных никак не обеспечивает аналитика информацией о том, действительно ли прибыльность проекта достаточно велика, чтобы как то компенсировать риск по проекту, оцененный стандартным отклонением и коэффициентом вариации.
Ряд исследователей избегает использования данного метода ввиду кажущейся сложности построения вероятностной модели и множества вычислений, однако при корректности модели метод дает весьма надежные результаты, позволяющие судить как о доходности проекта, так и о его устойчивости (чувствительности).
В зависимости от полученных результатов завершенного анализа рисков, а также и от того, насколько склонен к риску инвестор, последний принимает решение принять, изменить, или отклонить проект.
Например, инвестор, исходя из своей склонности к риску, действовал бы например следующим образом:
1. Риск >= 30%
В случае если показатель риска, а это, прежде всего нормированный ожидаемый убыток (НОУ), равен или превышает 30%, то для принятия данного проекта необходимо предварительно внести и осуществить предложения по снижению риска. Под предложениями понимаются любые действия по изменению данных на входе информации, способные уменьшить риск, не обрекая проект на убыточность.
В этих целях обычно используются:
Разработанные заранее правила поведения участников (игроков) в определенных “нештатных” ситуациях (например, сценарии, предусматривающие соответствующие действия участников при тех или иных изменениях условий реализации проекта).
В проектах могут предусматриваться также специфические механизмы стабилизации, обеспечивающие защиту интересов участников (игроков) при неблагоприятном изменении условий реализации проекта (в том числе в случаях, когда цели проекта будут достигнуты не полностью или же не достигнуты вообще) и предотвращающие возможные действия участников, ставящие под угрозу его успешную реализацию.
В одном случае может быть снижена степень самого риска как такого (за счет дополнительных затрат на создание резервов и запасов, совершенствование технологий, уменьшение аварийности производства, материальное стимулирование повышения качества продукции), в другом - риск перераспределяется между участниками (игроками) (индексирование цен, предоставление гарантий, различные формы страхования, залог имущества, система взаимных санкций).
Как правило, применение в проекте стабилизационных механизмов всегда требует от участников дополнительных затрат, размер которых обязательно зависит от условий реализации мероприятия, ожиданий и интересов участников, их оценок степени возможного риска. Такие затраты, конечно, подлежат обязательному учету при определении эффективности проекта.
Здесь должна работать балансировка между риском и прибыльностью. Если на этом этапе удается снизить риск так, что НОУ становится меньше 30%, и есть выбор среди такого рода вариантов проекта, то лучше выбрать тот из них, у которого коэффициент вариации меньше. Если же не удается снизить риск до указанной отметки, проект отклоняется.
2. Риск < 30%
Проекты с риском менее 30% (НОУ<30%) лучше подстраховать. Предлагается создать страховой фонд в размере определенной доли от основной суммы инвестирования. Как определить эту долю - это вопрос методики. Можно принять ее равной значению показателя риска (нормированный ожидаемый убыток).
То есть, например, если риск равен 25%, то необходимо, скажем, предусмотреть отчисления от нераспределенной прибыли в процессе осуществления проекта или заключить договор со страховой компанией на сумму в размере 25% от основной суммы инвестирования и направить эти деньги в резерв, подлежащий использованию только в случае наступления крайних ситуаций, связанных, например, с незапланированным недостатком свободных денежных средств, а также другими проблемами в целях нормализации финансово-экономической ситуации. На самом деле, источник оплаты страхового фонда, скорее всего, будет зависеть от периода осуществления проекта. В самый трудный в финансовом отношении начальный момент осуществления проекта у предприятия вряд ли найдется возможность обойтись без внешнего окружения при создании страхового фонда, например, на базе страховой компании. Но по мере осуществления проекта у предприятия накапливается прибыль, ежегодные отчисления от которой могли бы составить страховой фонд.
Проанализируем результативность анализа рисков:
Таблица 14.
Анализ рисков
| Полезность | Ограниченность |
| 1.Совершенствует уровень принятия решений по малоприбыльным проектам. Проект с малым значением NPV может быть принят, в случае если анализ рисков установит, что шансы получить удовлетворительный доход превосходят вероятность неприемлемых убытков. 2.Помогает идентифицировать производственные возможности. Анализ рисков помогает сэкономить деньги, потраченные на получение информации, издержки, на получение которой превосходят издержки неопределенности. 3.Освещает сектора проекта, требующие дальнейшего исследования и управляет сбором информации. 4.Выявляет слабые места проекта и дает возможность внести поправки. 5.Предполагает неопределенность и возможные отклонения факторов от базовых уровней. В связи с тем, что присвоение распределений и границ варьирования переменных несет оттенок субъективизма, необходимо критически подходить даже к результатам анализа рисков. | 1.Проблема коррелированных переменных, которые, если неправильно специфицированы, могут привести к обманчивым заключениям. 2. Анализ рисков предполагает доброкачественность моделей проектного оценивания. Если модель неправильна, то результаты анализа рисков также будут вводить в заблуждение. |
2.7.3. Использование метода Монте Карло для систем массового обслуживания
Повторимся - сущность метода Монте-Карло состоит в следующем: требуется найти значение, а некоторой изучаемой величины. Для этого выбирают какую то случайную величину Х, математическое ожидание которой равно а: М (Х)=а.
Практически чаще всего поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое 
и принимают 
в качестве оценки (приближённого значения) a* искомого числа a:
. (137)
Напомним, что поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний.
Итак пусть необходимо получить значения случайной величины 
, распределенной в интервале 
с плотностью 
. Давайте докажем, что значения можно найти из уравнения
, (138)
где 
– случайная величина, равномерно распределенная на интервале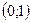 
. То есть, выбрав очередное значение надо решить уравнение и найти очередное значение . Для доказательства рассмотрим функцию:
(139)
Имеем общие свойства плотности вероятности:
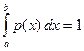(140)
Из формул следует, что 
, а производная 
.
Значит, функция 
монотонно возрастает от 0 до 1. И любая прямая 
, где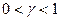 
, пересекает график функции 
в единственной точке, абсциссу которой мы и принимаем за . Таким образом, уравнение всегда имеет одно и только одно решение.
