Для получения первого столбца первого квадранта нужно элементы первого столбца заданной матрицы А умножить на величину Х2 = 775.3; элементы второго столбца матрицы А умножить на Х2= 510.1; элементы третьего столбца матрицы А умножить на Х3=729.6.
Составляющие третьего квадранта (условно чистая продукция) находятся как разность между объёмами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.
Наконец, четвертый квадрант в данном примере состоит из одного показателя и служит также для контроля правильности расчёта: сумма элементов второго квадранта должна в стоимостном материальном балансе совпадать с суммой элементов третьего квадранта. Результаты расчёта представлены в табл.10:
Таблица 10. Межотраслевой баланс производства и распределения продукции.
| Производящие отрасли | Потребляющие отрасли | ||||
| Конечная продукция | Валовая продукция | ||||
| 232.6 155.1 232.6 | 51.0 255.0 51.0 | 291.8 0.0 145.9 | 200.0 100.0 300.0 | 77.3 510.1 729.6 | |
| Условно чистая продукция | 155.0 | 153.1 | 291.9 | 600.0 | |
| Валовая продукция | 775.3 | 510.1 | 729.6 | 2015.0 |
Теперь расмотрим построение межотраслевого баланса затрат труда
Различные модификации рассмотренной выше модели межотраслевого баланса производства и распределения продукции в народном хозяйстве позволяют расширить круг показателей, охватываемых моделью. Рассмотрим в качестве примера применение межотраслевого баланса для анализа такого важного экономического показателя как труд.
Пусть в дополнение к исходным данным из первого параграфа данной главы заданы затраты живого труда (трудовые ресурсы) в трёх отраслях:
L1=1160, L2=460, L3=875.
Требуется определить коэффициенты прямой и полной трудоёмкости и составить межотраслевой баланс затрат труда.
1. коэффициенты прямой трудоёмкости (tj) представляют собой прямые затраты труда на единицу j-го вида продукции. Определить их можно как соотношение затрат живого труда в производстве j-го продукта (Lj) к объёму производства этого продукта, то есть к валовому выпуску (Xj) (11,249).
Воспользовавшись данной формулой получим:
t1 = 1160/775.3 =1.5 t2 = 460/510.1 =0.9 t3=875/730.6=1.2
2. коэффициенты полной материальных затрат определяются как произведение коэффициентов прямой трудоёмкости и матрицы коэффициентов полных материальных затрат (полученной в первом параграфе):
|| 2.041 0.612 1.020||
T = (1.5; 0.9; 1.2) * || 0.816 2.245 0.408||
|| 0.867 0.510 1.684||
3. Умножая первую, вторую и третью строки первого и второго квадрантов межотраслевого материального баланса, на соответствующие коэффициенты прямой трудоёмкости, получим схему межотраслевого баланса труда (в трудовых измерителях) (табл.11).
Таблица 11. Межотраслевой баланс затрат труда.
| Производящие отрасли | Потребляющие отрасли | ||||
| Межотраслевые затраты овеществленного труда | Затраты труда на конечную продукцию | Затраты труда в отраслях (трудовые ресурсы) | |||
| 348.9 139.6 279.1 | 76. 229.5 61.2 | 437.7 0.0 175.1 | 300.0 90.0 360.0 | 1163.0 459.1 875.5 |
Таким образом, поняв в общих чертах специфику определения затрат труда при использовании межотраслевого баланса, можно перейти к более сложному рассмотрению применения метода Леонтьева.
А вот методика прогнозирования структуры общественного производства на основе межотраслевого баланса
Итак теперь рассмотрим применение матриц прямых и полных затрат уже для прогнозирования структуры общественного производства. Именно прогнозированию функционирования экономики регионов или в целом страны, нужно уделять пристальное внимание особенно в данный момент. В данном случае представлены несколько устаревшие данные из Статистического Российского Ежегодника за 2011 год.
Исходные данные:
1. В 2011 г. объем конечного спроса на продукцию чистых отраслей российской экономики составил: в промышленности - 1454 трлн. руб., в строительстве - 354 трлн. руб., в остальных отраслях - 1006 трлн. руб.
2. Валовое накопление в объеме конечного спроса было равно: в промышленности - 192 трлн. руб., в строительстве - 345 трлн. руб., в остальных отраслях экономики - 24 трлн. руб.
3. Объем экспорта по отраслям составил: в промышленности - 506 трлн. руб., в строительстве - 1 трлн. руб., в остальных отраслях экономики - 44 трлн. руб.
4. Корректировочные статьи для перехода к использованию отечественных товаров и услуг в основных ценах (чистые налоги на продукты, торгово-посредническая и транспортная наценка) составили в итоге: в промышленности - 1368 трлн. руб., в строительстве - 46 трлн. руб., в остальных отраслях экономики - (-915) трлн. руб.
5. Матрица прогнозных коэффициентов прямых материальных затрат на рубль валового выпуска по отраслям составляет:
Рисунок 75.
Матрица прогнозных коэффициентов полных затрат на рубль конечного спроса составляет:
Рисунок 76.
6. Коэффициенты прямой фондоемкости валового выпуска (затраты производственных фондов на рубль продукции) по отраслям равны:
f= (2,475 0,921 3,638)
7. Коэффициенты затрат живого труда (человеко-часов) на 1000 рублей валового выпуска по отраслям равны:
t= (0,0162 0,0220 0,0311)
Нужно определить:
1. Объем валового выпуска по отраслям, необходимый для удовлетворения конечного спроса.
2. Объем валового выпуска по отраслям, необходимый для обеспечения валового накопления и потребления в структуре конечного спроса.
3. Коэффициенты полной фондоемкости и трудоемкости на рубль конечного спроса по данным отраслям.
4. Коэффициенты полной фондоемкости и трудоемкости на рубль валового накопления и потребления.
5. Объем производственных фондов и общие затраты труда, необходимые для обеспечения объема конечного спроса, валового накопления и потребления.
6. Объем межотраслевых поставок продукции.
7. Объем валовой добавленной стоимости по отраслям.
8. Составить межотраслевой баланс производство и распределения продукции и услуг (таблицу "Затраты - Выпуск").
РЕШЕНИЕ
Исходные данные:
f= (2,475; 0,921; 3,638); t=(0,0000162; 0,0000220; 0,0000311)
Рисунок 77.
Вспомогательные расчеты
Объем конечного потребления в структуре конечного спроса: 
Рисунок 78.
Величина конечного спроса с учетом корректирующих статей:
Рисунок 79.
Решение.
1. 
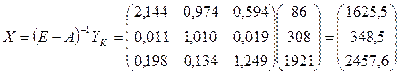трлн. руб.
Рисунок 80
Общий объем валового выпуска = 1625,5 + 348,5 + 2457,6 = 4431,6
2. 
трлн. руб.
Рисунок 81
Итого: 1227,1 трлн. руб.
трлн. руб.
Рисунок 82
Итого: 3542,3 трлн. руб.
3. 
4.
5. 
трлн. руб.
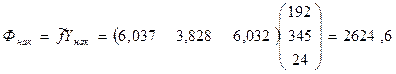трлн. руб.
трлн. руб.
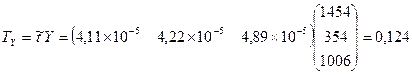трлн. чел.- часов
Рисунок 83.
(объем прямых затрат труда для обеспечения вал. выпуска = t х X = 0,110 трлн. чел.- часов)
трлн. чел.- часов
трлн. чел.- часов
4. 
4,678 руб. на 1 руб. валового накопления
6,024 руб. на 1 руб. конечного потребления
чел. - часов на рубль валового накопления
чел.- часов на рубль конечного потребления
Рисунок 85.
6. Объем межотраслевых поставок продукции (трлн. руб.) 
| 0,511 * 1625,5 = 830,6 | 0,442*348,5= 154,0 | 0,226 * 2457,6 = 555,4 |
| 0,004* 1625,5=6,5 | 0,004*348,5= 1,4 | 0,013 * 2457,6 =31,9 |
| 0,077* 1625,5= 125,2 | 0,037 * 348,5 = 12,9 | 0,162*2457,6=398,1 |
| Итого = 962,3 | Итого = 168,3 | Итого = 985,4 |
7. Z1 = X1 - 962,3 = 1625,5 - 962,3 = 663.2 трлн. руб.
Z2 = X2 - 168,3 = 348,5 - 168,3 = 180,2 трлн. руб.
Z3= Х3 - 985,4 = 2457,6 - 985,4 = 1472,2 трлн. руб.
Рисунок 86.
Итак, теперь исходя из по полученных результатов, можно составить схему межотраслевого баланса.
| Промышленность | Строительство | Другие отрасли | Всего использовано ресурсов на промежуточное потребление | Конечное потребление | Валовое накопление | Экспорт | Всего использовано ресурсов вценах покупателей | Корректировочные статьи (—) | Всего использовано отечественных ресурсов в основных ценах | |
| Промышленность | 830,6 | 154,0 | 555,4 | 1540,0 | ||||||
| Строительство | 6,5 | 1,4 | 31,9 | 39,8 | 393,8 | 347,8 | ||||
| Другие отрасли | 125,2 | 12,9 | 398,1 | 536,2 | 1542,2 | -915 | 2457,2 | |||
| Промежуточное потребление — всего | 962,3 | 168,3 | 985,4 | 2116,0 | ||||||
| Валовая добавленная стоимость (в основных ценах) | 663,2 | 180,2 | 1472,2 | 2315,6 | ||||||
| Выпуск товаров и услуг (в основных ценах) | 1625,5 | 348,5 | 2457,6 | 4431,6 |
Таблица 12. Схема межотраслевого баланса (в ценах покупателей)
Итак, можно сделать следующие краткие выводы:
1. Аналитический метод «затраты выпуск» наполнил практическим содержанием теорию общего экономического равновесия, он способствовал усовершенствованию математического аппарата. Так динамическая модель Леонтьева раскрыла некоторую ограниченность статичной математической модели одного из основоположников неоклассической экономической школы Л Вальраса.
2. Метод Леонтьева отличает ясность и простота, универсальность и глобальность, другими словами пригодность как для экономики отдельных стран и регионов, так и для мирового хозяйства в целом.
Модели В. Леонтьева, и межотраслевой анализ может служить основным инструментом стратегического планирования.
3. В настоящее время в национальной экономике существуют и продолжают возникать сложные проблемы, требующие межотраслевых обоснований. Использование же метода “затраты - выпуск” межотраслевого баланса позволяет не только изучить взаимозависимость между различными отраслями экономики, проявляющуюся во взаимовлиянии цен, объемов производства, капиталовложений и доходов, но и решать следующие задачи:
- прогноз основных макроэкономических показателей (выпуск валового и конечного продукта, чистая продукция, материальные затраты, производственное потребление продукции и другие в разрезе отраслей материального производства) в зависимости от изменения как внешних, так и внутренних факторов;
- прогноз динамики оптовых цен продукции, а также уровня инфляции, и стоимости потребительской корзины;
- прогноз уровня безработицы и занятости;
- прогноз экологической обстановки и оценка затрат на проведение природоохранных мероприятий;
- оценка эффективности предложений по размещению производительных сил;
- оценка эффективности межрегиональных связей;
- и так далее и тому подобное.
Таким образом, на основе моделей В. В. Леонтьева может быть разработан комплекс моделей функционирования экономики с целью разработки рациональных стратегий управления социально-экономическим развитием региона и страны в целом.
Таблица 13. Схема статического межотраслевого баланса.
| Производящая отрасль | Потребляющая отрасль | Продукция. | |||||
| j | n | Конечная | Валовая | ||||
| x11 | x12 | x13 | … | x1n | y1 | X1 | |
| x21 | x22 | x23 | … | x2n | y2 | X2 | |
| x31 | x32 | x33 | … | x3n | y3 | X3 | |
| I | … | … | … | I … | … | II... | … |
| N | xn1 | xn2 | xn3 | … | xnn | yn | Xn |
| Оплата труда | v1 | v2 | v3 | … | vn | vкон | - |
| Чистый доход | m1 | m2 | m3 | … | mn | mкон | - |
| Амортизация | с1 | с2` | с3 | III … | сn | IV | - |
| Валовая продукция | X1 | X2` | X3 | … | Xn | - | ∑Xi=∑Xj |
Примечания: 1. в I квадранте – а11, а12, а13 и.т.д. (удельные коэффициенты); 2. Во II квадранте – С (личное потребление); I (инвестиции); G (гос. закупки); X (экспорт); 3. В III квадранте – W (зарплата); P (прибыль, процент, рента); M (импорт).
Модель В. В. Леонтьева отвечает на вопрос: можно ли в условиях данной технологии удовлетворить конечный спрос? Ответ на этот вопрос сводится к существованию конуретного решения системы относительно переменных. Условия существования и единственности решения такой системы хорошо известны из курса линейной алгебры. Однако здесь речь идет о решении этой системы, имеющем реальный экономический смысл. А именно, все элементы модели В. В. Леонтьева, по их определению, являются неотрицательными величинами, в том числе переменные. Поэтому мы обязаны говорить о существовании неотрицательных решений системы.
Определение: Модель В. В. Леонтьева называется продуктивной, если система имеет неотрицательное решение.
Матрица называется невырожденной, если она имеет обратную матрицу, определяемую условиями. Обратная матрица существует и неотрицательна, если все главные миноры матрицы B положительны (условие Хокинса-Саймона):
Справедливы следующие утверждения.
Теорема: Матрица D системы, элементы которой удовлетворяют условиям, неотрицательно обратима тогда и только тогда, когда уравнение имеет неотрицательное решение (т.е. продуктивно).
(Квадратная матрица D называется неотрицательно обратимой, если она невырожденна и ее обратная матрица неотрицательна).
Теорема: Уравнение продуктивно тогда и только тогда, когда матрица
удовлетворяет условию Хокинса - Саймона, то есть все главные ее миноры положительны.
Из приведенных утверждений следует, что необходимым и достаточным условием продуктивности модели В. В. Леонтьева является существование неотрицательно обратимой матрицы, то есть, чтобы матрица была невырожденна и обратная матрица была неотрицательна.
Итак, если эти условия выполнены, то искомый вектор выпуска x определяется по формуле. Матрица предоставляет информацию о том, каким образом вектор конечного спроса с пересчитывается в необходимый вектор валового выпуска x. Из линейности модели В. В. Леонтьева по x и c следует, что приращение вектора c и соответствующее приращение вектора x связаны между собой уравнением.
Следовательно, матрица позволяет вычислить системное изменение валового выпуска, вызванное изменением конечного потребления. Поэтому матрицу часто называют матричным мультипликатором. Элемент матричного мультипликатора можно интерпретировать так - это количество продукта одного вида, необходимое для выпуска одной единицы продукции другого вида.
Известно, что такие матрицы можно представить в виде степенного ряда матриц:
Видим, что вычисление (аппроксимация) обратной матрицы связано со
сходимостью бесконечного степенного ряда.
Если матрица неотрицательно обратима, то ряд сходится, то есть сумма конечна.
Подведя итоги сказанного, мы можем утверждать, что для продуктивной модели В. В. Леонтьева вектор валового выпуска x представляется матричным рядом
Важным следствием модели В. В. Леонтьева являются результаты, получаемые с применением двойственной к ней модели где - транспонированная матрица. Уравнению можно придать смысловую стоимостную окраску. Действительно, можно интерпретировать как вектор цен продуктов отраслей, - как вектор добавленной стоимости (то есть прибавка к стоимости товара после ее производства) на единицу выпуска, - как вектор суммы издержек на единицу выпуска. Тогда разность есть вектор чистого дохода от единицы выпуска. Этот чистый доход и приравнивается добавленной стоимости.
Существование решения двойственного уравнения относительно вектора цен связано опять с неотрицательностью всех его элементов.
Если уравнение имеет неотрицательное решение, то двойственная модель В. В. Леонтьева называется прибыльной. Это свойство является двойственным к понятию продуктивности модели В. В. Леонтьева в том смысле, что выполнение одного из свойств оюязательно влечет справедливость другого. Данное положение является следствием наличия тесной математической связи между взаимно двойственными уравнениями.
Теорема: Для того чтобы модель затраты - выпуск В. В. Леонтьева была продуктивной, необходимо и достаточно, чтобы двойственная к ней модель была прибыльной.
Мы здесь рассмотрели классическую (исходную) модель В. В. Леонтьева, которая описывает производство по схеме затраты-выпуск. Значимость модели В. В. Леонтьева заключается еще и в том, что она применяется для описания ряда других экономических задач, а также служит отправной точкой для различных обобщений.
При трактовке уравнения как модели торговли n означает число торгующих между собой стран, - национальный доход i-ой страны, - национальные расходы i –ой страны, - объем импорта из страны i в страну j, приходящийся на одну единицу национального дохода страны j. Элементу придается смысл коэффициента внутреннего потребления своей продукции i -ой страной.
И в такой интерпретации, очевидно, все элементы модели В. В. Леонтьева должны быть неотрицательными и, более того, национальный доход и национальные затраты всегда являются положительными величинами. В данном случае модель дает ответ на вопрос: каковы должны быть объемы национальных доходов стран, обеспечивающие стабильный уровень национальных расходов и установившийся режим обмена товарами между странами?
Выше уже было замечено, что одним из существенных упрощений модели В. В. Леонтьева является отсутствие в ней первичных (невозобновляемых) факторов производства.
Модель будет более близкой к реальности, если наряду с воспроизводимыми (вторичными) ресурсами, описываемыми в произведением Ax, будут учтены и первичные факторы. Так вот оказывается, что такое обобщение превращает модель В. В. Леонтьева в оптимизационную задачу.
Предположим, что в модели каждый товар производится с использованием продукций всех отраслей и еще m видов первичных ресурсов. Обозначим через количество k-го первичного фактора, затрачиваемого в производство xj количества j-го товара, а через - количество k -го первичного фактора, необходимое для производства одной единицы товара вида j.
Таким образом, для каждого товара j мы имеем n+m видов представления его выпускаемого объема:
Поэтому производство во всех n отраслях может быть описано n линейными производственными функциями.
Суммируя обе части этих уравнений по j, получим выражения, определяющие суммарные по всем отраслям объемы затрат вторичных и первичных факторов производства:
Так как уравнения относятся к товарам каждой отрасли, используемым как на производственное, так и на конечное потребление, должно быть или в матричной форме.
Введем в рассмотрение матрицу, трактуемую как технологическая матрица для первичных ресурсов, и предположим, что известен вектор запасов всех первичных ресурсов.
Поставим следующий вопрос: при каком векторе выпуска реализация конечного продукта приведет к максимальному доходу с учетом наличного запаса первичных ресурсов? В ответ получаем задачу линейного программирования.
Так как по смыслу задачи максимизация дохода осуществляется через вектор выпуска, эту задачу целесообразно переписать, выразив в целевой функции вектор спроса c
Решение задачи дает вектор спроса на товары, а решение задачи
- вектор предложения первичных факторов. Для пары задач и их решений c и v верны все утверждения для двойственных задач линейного программирования.
Согласно общего определения равновесия, набор будет равновесным в модели Леонтьева, если выполнены соотношения.
Благодаря линейности задач, такое равновесие существует.
2.6. Теория массового обслуживания
Теория систем массового обслуживания (СМО) или теория очередей, начала развиваться в начале 20 века. Основателем СМО считается математик Иохансен, сформулировавший в 1907 году теоретические предпосылки новой теории.
Первые практические задачи теории массового обслуживания были рассмотрены сотрудником Копенгагенской телефонной компании, инженером Эрлангом (1878—1929) в период между 1908 и 1922 годами. Целью решения задач было упорядочить работу телефонной станции и заранее рассчитать качество обслуживания потребителей (очередь в ожидании) в зависимости от числа используемых устройств. В 1909 году Эрланг применил теорию вероятностей к исследованию зависимости обслуживания телефонных связей от числа поступающих на телефонную станцию вызовов. До сих пор эти идеи используются провайдерами сотовой связи.
В СССР развитием данной проблематики занимался математик Хинчин, одной из главных работ которого, является «Теория очередей».
Теория систем массового обслуживания посвящена разработке методов анализа, проектирования и рациональной организации систем, относящихся к различным областям деятельности, таким как связь, вычислительная техника, экономика, системы управления и организация производства, транспорт, торговля, здравоохранение, военное дело, логистика. Несмотря на все свое разнообразие, все приведенные системы обладают рядом типичных свойств, а именно:
· СМО представляют собой системы определенного специфического вида. Под системой понимается совокупность взаимосвязанных и целенаправленно взаимодействующих частей (элементов).
· СМО (системы массового обслуживания) - это модели системы, в которых с одной стороны возникают массовые запросы (требования) на выполнение каких-либо услуг, а с другой стороны происходит удовлетворение этих запросов.
· СМО представляет собой совокупность обслуживающего оборудования и персонала при соответствующей организации процесса обслуживания.
· Задать СМО значит задать структуру системы и статистические характе-ристики последовательности поступления заявок и последовательности их обслуживания.
Каждая система массового обслуживания состоит из какого-то числа обслуживающих устройств, приборов, линий связи, кассовых аппаратов и тому подобное, восполняющих определенные операции. Все они в дальнейшем (тра-диционно) будут называться каналами обслуживания.
Обслуживанию подлежит поток заявок или требований, поступающих в системы. Заявки поступают чаще всего в случайные моменты времени. Длительность обслуживания каждой заявки так же является случайной величиной. В связи с этим работа системы протекает нерегулярно. В какие-то моменты каналы обслуживания простаивают, в другие моменты происходит накапливание заявок. Это приводит либо к отказу обслуживания каких-то заявок, либо к образованию из них очередей.
Для уменьшения степени влияния подобных негативных факторов разрабатываются рекомендации по создпнию рациональной организации системы в соответствии с требуемой пропускной способностью и другими характеристиками эффективности ее работы. Разработка подобных конкретных рекомендаций и методов расчета характеристик эффективности систем и есть предмет теории массового обслуживания.
Системы массового обслуживания (СМО)— это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.
С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания.
Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.
Примерами систем массового обслуживания могут служить:
1. магазины;
2. банки;
3. ремонтные мастерские;
4. почтовые отделения;
5. посты технического обслуживания автомобилей, посты ремонта автомобилей;
6. персональные компьютеры, обслуживающие поступающие заявки или требования на решение тех или иных задач;
