Определение момента инерции тел

Цель работы: определить с помощью крутильного маятника зависимость момента инерции тела от расстояния до оси вращения, проверить выполнение теоремы Штейнера.

Оборудование: крутильный маятник, секундомер, исследуемое тело (составной цилиндр).

 

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

 

Момент инерции – это физическая величина, являющаяся мерой инертности тела при его вращательном движении. В этом смысле он подобен массе, являющейся мерой инертности тела при поступательном движении. Величина момента инерции, по определению, равна сумме произведений масс частиц тела на квадраты их расстояний r до оси вращения:

J = S m _i r_i² или J = ò r ² dm. (1)

 

Величина момента инерции тела зависит не только от массы тела, но и от расположения частей тела относительно оси вращения. Чем дальше от оси находятся части тела, тем больше момент инерции.

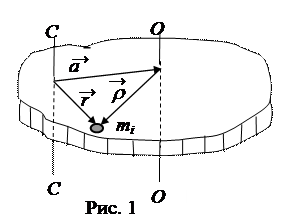Теоретический расчет момента инерции тел упрощается при применении теоремы Штейнера. Получим уравнение теоремы. Пусть точка О – центр масс тела, через которую проходит ось О – О, а параллельно ей на некотором расстоянии а ось С− С (рис. 1). Установим связь между моментами инерции тела относительно этих осей. Представим вектор от оси С–С до некоторого элемента массы m _i как сумму векторов 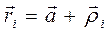(рис. 1). Подставив в определяющую формулу момента инерции (1) радиус - вектор r и возведя сумму в квадрат, получим

 

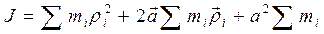. (2)

Первый член этого уравнения J ₀ – момент инерции тела относительно оси О – О, проходящей через центр масс. Во втором члене сумма определяет положение центра масс тела относительно оси О – О, и так как ось проходит через центр масс, то эта сумма равна нулю. Третий член – это произведение суммы масс частиц, то есть массы тела, на квадрат расстояния между осями. Итак,

 

J = J ₀ + m a ². (3)

 

Это уравнение теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, и произведению массы тела на квадрат расстояния между осями. В тех случаях, когда момент инерции относительно оси, проходящей через центр масс J ₀ , можно сравнительно легко рассчитать, теорема Штейнера позволяет определить момент инерции относительно произвольной оси J, избежав весьма трудоемких расчетов. Теорему Штейнера можно экспериментально проверить, если измерить момент инерции тела при разных расстояниях от оси вращения до центра масс тела. Если зависимость J от a ² будет линейной с угловым коэффициентом, равным массе тела, то теорема верна.

Одним из методов измерения момента инерции тел является метод крутильного маятника. Крутильный маятник – это тело, произвольной формы, подвешенное на упругих струнах. В лабораторной установке – это рамка (рис.1). Если рамку отклонить от положения равновесия и отпустить, то она под действием момента упругих сил струны (M =−kα) возвращается к положению равновесия,но по инерции проходит положение равновесия, закручивая струну в противоположном направлении. Возникают вращательные колебания. Применим основной закон динамики вращательного движения: произведение момента инерции рамки на угловое ускорение равно моменту упругих сил подвеса:

 

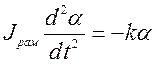. (4)

 

Это дифференциальное уравнение второго порядка. Его решением должна быть функция, обращающая его в тождество. Например, это может быть функция косинус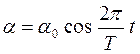а: , где Т – период колебаний. Подставив функцию в уравнение (4), получим, что она будет решением, при условии, если период колебаний маятника равен

 

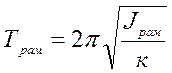. (5)

Исследуемое тело представляет собой составной цилиндр из двух половин, полуцилиндров. Наденем их на стержень на одинаковом расстоянии а от оси(рис. 2). Момент инерции маятника изменится и будет равен сумме момента инерции рамки и исследуемого цилиндра. Период тоже изменится и станет равным

 

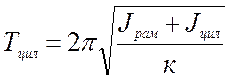. (6)

 

Решая совместно уравнения (5) и (6), исключая коэффициентупругости подвеса к, получим формулу для экспериментального определения момента инерции цилиндра по известному моменту инерции рамки

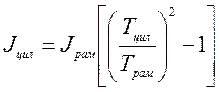. (7)

 

ВЫПОЛНЕНИЕ РАБОТЫ

 

1. Убедиться, что флажок рамки при колебаниях не задевает фотоэлемент. Снять полуцилиндры со стержня, определить массу цилиндра (как суммарную массу половин). Записать массу и момент инерции рамки, указанный на установке, в табл. 1.

Включить установку в сеть 220 В, нажать кнопку Сеть на задней стенке секундомера.

2. Определить период колебаний ненагруженной рамки Т_р. Для этого отвести рамку к электромагниту. Магнит притянет рамку. Нажать кнопку Пуск. Магнит отпустит рамку. Начнется счет времени и числа колебаний. Чтобы измерить время десяти колебаний t следует после совершения девятого колебания нажать кнопку Стоп. Период равен T_р=t/ 10. Результат записать в табл. 1.

Таблица 1

Момент инерции Jрам, кг∙м2	0,815∙10-4
Масса цилиндра mцил, кг
Период колебаний, Трам, с

3. Надеть на стержень полуцилиндры, расположить симметрично вплотную в центре и закрепить. Расстояние между центром составного цилиндра и осью будет равно половине толщины полуцилиндра. Нажать кнопку «Сброс» для обнуления индикаторов. Отвести рамку к магниту. Нажать кнопку Пуск. Определить период колебаний Т _цил .

4. Сместить оба полцилиндра от оси по стержню на одинаковое расстояние в противоположные стороны. Измерить расстояние между осью маятника и серединой полуцилиндров. Измерить соответствующий период колебаний. Опыт повторить не менее пяти раз во всём интервале расстояний а. Результаты записать в табл. 2.

Выключить установку.

Таблица 2

 

Расстояние а, см
Период с цилиндром Тцил, с
Момент инерции Jцил, кг/м2
Квадрат расстояния а 2, м2

5. Произвести расчеты в системе СИ. Рассчитать момент инерции цилиндра по формуле (7) для различных расстояний полуцилиндров от оси. Рассчитать квадраты расстояний а². Записать в табл. 2.

6. Построить график зависимости момента инерции цилиндра от квадрата расстояния цилиндра от оси а ². Размер графика не менее половины страницы.

Около точек провести прямую линию так, чтобы сумма отклонений была минимальна. Построить на экспериментальной линии, как на гипотенузе, треугольник (рис. 3). Определить угловой коэффициент линии по координатам вершин А, В

 

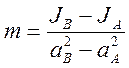. (8)

 

6. Сравнить полученное значение углового коэффициента m с массой составного цилиндра m_цил. Оценить относительную погрешность выполнения теоремы Штейнера

 

.

 

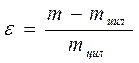7. Сделать выводы.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Дайте определение момента инерции тела, его физический смысл.

2. Выведите и сформулируйте теорему Штейнера и условия ее применения.

3. Выведите формулу для периода колебаний рамки маятника.

4. Выведите формулу для экспериментального определения момента инерции исследуемого цилиндра по измеренным периодам колебаний маятника и маятника с цилиндром.

5. При каких условиях может быть подтверждена теорема Штейнера?

6. С какой целью определяют угловой коэффициент экспериментальной линии на графике J (a ²)?

Работа 7