÷ель работы: проверить выполнение основного закона динамики вращательного движени€, определить момент инерции ма€тника ќбербека.
ќборудование: ма€тник ќбербека, секундомер, грузы.
“≈ќ–≈“»„≈— ќ≈ ¬¬≈ƒ≈Ќ»≈
¬ращательное движение тела вокруг неподвижной оси Ц это движение, при котором траектории всех точек тела €вл€ютс€ концентрическими окружност€ми, центры которых лежат на линии, €вл€ющейс€ осью вращени€. ѕараметрами вращательного движени€ тела €вл€ютс€: угловой путь j, то есть угол поворота тела вокруг оси; углова€ скорость w =  ; и угловое ускорение e =
; и угловое ускорение e =  . Ёто аксиальные векторы, то есть векторы, направленные по оси вращени€. ≈сли вращать буравчик вместе с телом, то направление его поступательного движени€ вдоль оси совпадает с вектором угловой скорости.
. Ёто аксиальные векторы, то есть векторы, направленные по оси вращени€. ≈сли вращать буравчик вместе с телом, то направление его поступательного движени€ вдоль оси совпадает с вектором угловой скорости.
”гловое ускорение тела ε, согласно основному закону динамики вращательного движени€, пр€мо пропорционально моменту силы M, действующему на тело,и обратно пропорционально моменту инерции тела относительно оси:
 . (1)
. (1)
ћомент силы по определению Ц это вектор, равный векторному произведению радиус-вектора точки приложени€ силы на вектор
силы:  . ¬еличину проекции вектора момента силы на ось вращени€ можно определить как произведение величины силы на ее плечо:
. ¬еличину проекции вектора момента силы на ось вращени€ можно определить как произведение величины силы на ее плечо:
ћ = F d. (2)
ѕлечо силы d Ц это длина перпендикул€ра, опущенного из оси вращени€ на линию действи€ силы. Ќаправление вектора момента силы относительно оси также определ€етс€ правилом буравчика: это аксиальный вектор, направленный в сторону поступательного движени€ буравчика под воздействием сил, действующих на ручки.
ћомент инерции по определению Ц это скал€рна€ физическа€ величина, равна€ сумме произведений масс частиц тела mi (или dm)на квадраты их рассто€ний r до оси вращени€:
J = å m i r i 2, или 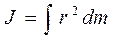 . (3)
. (3)
‘изический смысл момента инерции можно установить по уравнению (1). Ёто мера инертности тела при вращательном движении. „ем больше момент инерции тела, тем меньше его угловое ускорение при действии того же момента сил. ¬ этом смысле он €вл€етс€ аналогом массы, €вл€ющейс€ мерой инертности тела при поступательном движении. Ќо момент инерции зависит не только от массы, но и от ее распределени€. „ем дальше от оси вращени€ наход€тс€ части тела, тем больше момент инерции, тем меньше угловое ускорение, тем медленнее раскручиваетс€ или тормозит вращающеес€ тело.
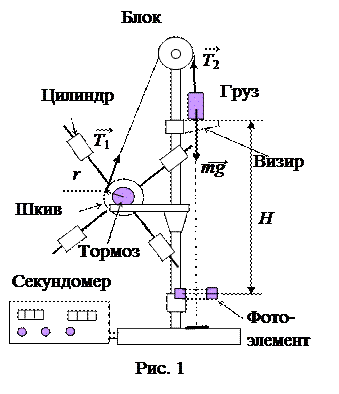
»зучение закономерностей вращательного движени€ в работе производитс€ с помощью ма€тника ќбербека (рис.1). ќн представл€ет собой крестовину, котора€ может вращатьс€ вокруг оси. Ќа спицах крестовины расположены цилиндры. Ќа шкив ма€тника наматываетс€ нить, на конце которой подвешен груз массы m. ¬ращение крестовины происходит под воздействием момента силы нат€жени€ нити  , где r Ц радиус шкива, €вл€ющийс€ плечом силы нат€жени€.
, где r Ц радиус шкива, €вл€ющийс€ плечом силы нат€жени€.
ƒл€ подтверждени€ основного закона динамики вращательного движени€ (1) следует независимо определить момент силы нат€жени€ нити и угловое ускорение крестовины ма€тника и убедитьс€ в том, что они пропорциональны друг другу. оэффициент пропорциональности равен величине, обратной моменту инерции 1/ J.
|
|
|
—илу нат€жени€ нити определим из уравнени€ второго закона Ќьютона дл€ груза, движущегос€ под действием силы т€жести mg и силы нат€жени€ нити:
m a = mg Ц T 2. (4)
ќткуда T 2 = m (g Ц a). “огда момент силы нат€жени€ нити можно рассчитать по формуле M = m (g Ц a) r. ¬ лабораторной установке ускорение падени€ груза много меньше ускорени€ свободного падени€, a<<g. ѕоэтому момент силы, вращающий крестовину, можно определить достаточно точно по приближенной формуле
M = mgr. (5)
”гловое ускорение e крестовины св€зано с тангенциальным ускорением точек поверхности шкива радиусом соотношением a = e r. “акое же ускорение имеет груз. ƒл€ экспериментального определени€ ускорени€ груза применим уравнение кинематики равноускоренного движени€  . “огда угловое ускорение крестовины можно определить по формуле
. “огда угловое ускорение крестовины можно определить по формуле
 , (6)
, (6)

где Ќ Ц высота падени€ груза; t Ц врем€ падени€; r Ц радиус шкива.
ќсновной закон динамики будет подтвержден, если на построенном графике зависимости углового ускорени€ крестовины от момента силы экспериментальные точки будут близко расположены относительно линии пр€мо пропорциональной зависимости.
Ќа самом деле существует момент сил трени€ в подшипниках оси, и экспериментальна€ пр€ма€ будет смещена по оси абсцисс на величину момента сил трени€. ќднако угловой коэффициент теоретической и экспериментальной линий будет одинаков. Ёто позвол€ет определить среднее значение момента инерции крестовины графическим методом как отношение катетов пр€моугольного треугольника, построенного на экспериментальной линии как на гипотенузе (рис. 2):
 . (7)
. (7)
¬џѕќЋЌ≈Ќ»≈ –јЅќ“џ
1. ”бедитьс€, что крестовина сбалансирована и не вращаетс€ при ненат€нутой нити. ѕри необходимости сместить цилиндры на спицах и закрепить. ”становить визир на некоторой высоте. »змерить высоту H падени€ груза по шкале как рассто€ние между визиром и лучом фотоэлемента. »змерить радиус выбранного шкива r. »змерить рассто€ние от оси до цилиндров l. –езультаты записать в табл. 1.
“аблица 1 “аблица 2
| ¬ысота падени€ Ќ, см | |
| –адиус шкива r, мм | |
| –ассто€ние до цилиндров l, см |
| m, г | t, c | e, рад/с | M, Ќ∙м |
2. ”становить наименьший груз, определить его массу. Ќамотать нить на шкив, враща€ крестовину, так чтобы дно груза оказалось на уровне визира. ¬ключить установку в сеть 220 ¬.
Ќажать кнопку —еть (на задней панели), при этом будет включен электромагнитный тормоз. Ќажать кнопку ѕуск. “ормоз отпустит крестовину, начнетс€ счет времени секундомером. ¬ момент перекрыти€ грузом луча фотоэлемента счет прекратитс€, тормоз остановит вращение. «аписать массу груза и врем€ падени€ в табл. 2. ¬ыключить секундомер кнопкой Ђ—етьї дл€ отключени€ тормоза.
3. ¬раща€ крестовину, снова подн€ть груз к визиру. —нова включить секундомер кнопкой —еть. ѕовторить измерени€ времени падени€ груза не менее шести раз, увеличива€ разновесами массу груза. «аписать суммарную массу грузов и врем€ падени€ в каждом опыте в табл.2.
|
|
|
¬ыключить установку.
4. ѕроизвести расчеты в системе —». ќпределить по формулам (5) и (6) угловое ускорение крестовины e и момент силы нат€жени€ нити ћ в каждом опыте. –езультаты записать в табл. 2.
5. ѕостроить график зависимости углового ускорени€ крестовины от момента силы нат€жени€. –азмер графика не менее половины страницы, на ос€х координат указать равномерный масштаб. ѕровести около точек пр€мую линию так, чтобы отклонени€ точек от экспериментальной линии были минимальны.
6. ѕостроить на экспериментальной линии как на гипотенузе пр€моугольный треугольник (рис. 2). ѕо координатам вершин ј и ¬ по формуле (7) рассчитать среднее значение момента инерции < J >.
7. ќценить случайную погрешность измерени€ графическим методом (рис. 2)
 . (8)
. (8)
8. «аписать результат в виде J = < J > ± d J, – = 0,90. ќценить разумность результата, сравнив его среднее значение по пор€дку величины с расчетным значением момента инерции четырех цилиндров
Jцил = 4 mцил l 2 . —делать выводы.
ќЌ“–ќЋ№Ќџ≈ ¬ќѕ–ќ—џ
1. —формулируйте основной закон динамики вращательного движени€.
2. ƒайте определение момента силы. „ему равен момент силы, действующий на крестовину ма€тника?
3. ƒайте определение момента инерции, каков его физический смысл? ќт чего зависит момент инерции?
4. ак изменитс€ момент инерции, угловое ускорение крестовины, если цилиндры на спицах сместить ближе к оси?
5. ќт каких параметров зависит угол наклона экспериментальной линии на графике e (M)?
6. ак изменитс€ момент силы нат€жени€ и угловое ускорение крестовины при увеличении массы груза в чашке?
–абота 5
ќѕ–≈ƒ≈Ћ≈Ќ»≈ — ќ–ќ—“» ѕ”Ћ»
–”“»Ћ№Ќџћ ћјя“Ќ» ќћ
÷ель работы: определить скорость пули с помощью крутильно-баллистического ма€тника, познакомитьс€ с применением закона сохранени€ момента импульса.
ќборудование: крутильно-баллистический ма€тник с мишенью, пружинный пистолет, пул€, секундомер.
“≈ќ–≈“»„≈— ќ≈ ¬¬≈ƒ≈Ќ»≈
ќдним из способов определени€ скорости пули €вл€етс€ способ с применением крутильно-баллистического ма€тника. Ёто обусловлено тем, что после удара ма€тник поворачиваетс€ на угол, пропорциональный моменту импульса и скорости пули. рутильно-баллистический ма€тник Ц это массивное по сравнению с пулей тело произвольной формы, подвешенное на упругих нит€х.
ѕусть горизонтально лет€ща€ пул€ на рассто€нии r от оси попадает в мишень ма€тника и застревает в ней (рис. 1). ѕосле удара ма€тник и пул€ поворачиваютс€ совместно, и это €вл€етс€ признаком неупругого удара. “ак как процесс удара €вл€етс€ кратковременным, то за врем€ удара ма€тник не успевает повернутьс€ и силы упругости еще незакрученных нитей подвеса отсутствуют. ƒействуют только сравнительно большие внутренние силы удара. «начит, система тел пул€ Ц ма€тник на врем€ удара €вл€етс€ замкнутой. ѕоэтому выполн€етс€ закон сохранени€ момента импульса: в замкнутой системе тел сумма моментов импульсов тел посто€нна или сумма моментов импульсов тел до взаимодействи€ тел равна сумме моментов импульсов тел после взаимодействи€:  .
.
ћоментом импульса твердого тела относительно оси называетс€ аксиальный вектор, то есть вектор, направленный по оси вращени€, равный произведению момента инерции тела на вектор угловой скорости: 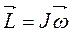 . ћоментом импульса материальной точки называют вектор, равный векторному произведению радиус-вектора точки r на вектор импульса
. ћоментом импульса материальной точки называют вектор, равный векторному произведению радиус-вектора точки r на вектор импульса  . ћомент импульса Ц это аксиальный вектор, направленный по оси вращени€ согласно правилу буравчика, как и вектор угловой скорости. ≈сли вращать буравчик вместе с телом, то вектор угловой скорости совпадает по направлению с поступательным движением буравчика.
. ћомент импульса Ц это аксиальный вектор, направленный по оси вращени€ согласно правилу буравчика, как и вектор угловой скорости. ≈сли вращать буравчик вместе с телом, то вектор угловой скорости совпадает по направлению с поступательным движением буравчика.
 ѕулю, размер которой много меньше рассто€ни€ от линии полета до оси вращени€ ма€тника r, можно считать материальной точкой. ѕо закону сохранени€ момента импульса момент импульса пули до удара будет равен моменту импульса ма€тника с застр€вшей пулей после удара. ¬ проекции на ось вращени€ уравнение будет иметь вид
ѕулю, размер которой много меньше рассто€ни€ от линии полета до оси вращени€ ма€тника r, можно считать материальной точкой. ѕо закону сохранени€ момента импульса момент импульса пули до удара будет равен моменту импульса ма€тника с застр€вшей пулей после удара. ¬ проекции на ось вращени€ уравнение будет иметь вид
|
|
|
mV r = (mr2 + J) w 0. (1)
≈сли пренебречь добавкой момента инерции пули mr 2 к моменту инерции ма€тника, то уравнение закона сохранени€ момента импульса будет иметь более простой вид: mVr = Jw 0. ќтсюда получим формулу дл€ скорости пули
 . (2)
. (2)
”гловую скорость w 0 ма€тника и момент инерции J можно определить из уравнени€колебаний. ≈сли ма€тник вывести от положени€ равновеси€ и отпустить, то он под действием момента упругих сил подвеса будет поворачиватьс€ к положению равновеси€, но по инерции пройдет его и отклонитс€ в противоположную сторону. «атем процесс повторитс€, возникнут вращательные колебани€. ”равнение основного закона динамики вращательного движени€ имеет вид: произведение момента инерции ма€тника на угловое ускорение 
 равно моменту упругих сил подвеса ћ = −ka:
равно моменту упругих сил подвеса ћ = −ka:
 . (3)
. (3)
–ешением дифференциального уравнени€ €вл€етс€ функци€, превращающа€ его в тождество. Ёто могут быть функции косинуса или
синуса
 , (4)
, (4)
где a 0Ц амплитуда колебаний, то есть наибольший угол отклонени€ ма€тника; “ 0 Ц период колебаний, то есть врем€ одного колебани€. ≈сли подставить функцию (4) в уравнение (3), то оно обратитс€ в тождество при условии, если период колебаний ма€тника будет равен
 . (5)
. (5)
»з этой формулы момент инерции определить пока невозможно, так как неизвестен коэффициент упругости подвеса k. „тобы его исключить, наденем на штыри рамки два груза с массой mгр на рассто€нии l от оси. ћомент инерции ма€тника измен€етс€ на величину, 2 mгр l 2. ѕериод колебаний ма€тника тоже изменитс€ и станет равным
 . (6)
. (6)
–еша€ уравнени€ (6) и (5), исключив коэффициент k, получим формулу дл€ момента инерции
 . (7)
. (7)
ѕолучим формулу дл€ расчета угловой скорости ма€тника. ”глова€ скорость, по определению, равна первой производной от угла поворота по времени. ƒифференциру€ уравнение (4), получим  . ќтсюда углова€ скорость ма€тника сразу после удара, при t = 0, может быть рассчитана по формуле
. ќтсюда углова€ скорость ма€тника сразу после удара, при t = 0, может быть рассчитана по формуле
 . (8)
. (8)
рутильный ма€тник представл€ет собой рамку, подвешенную к кронштейну на стальных струнах. ¬ыстрел пулей производитс€ с помощью пружинного пистолета. ”гол отклонени€ штанги ма€тника определ€етс€ по шкале по положению флажка на штанге. ѕериод колебаний определ€етс€ с помощью секундомера, управл€емого фотоэлементом.
¬џѕќЋЌ≈Ќ»≈ –јЅќ“џ
1. ”бедитьс€, что лини€ полета пули проходит через мишень, рамка может колебатьс€, не задева€ фотоэлемент; в положении равновеси€ флажок рамки находитс€ против нул€ шкалы. ѕри необходимости отрегулировать. —н€ть добавочные грузы.
2. ¬звести пружинный пистолет с пулей. ѕроизвести выстрел в мишень. »змерить угол первого отклонени€ ма€тника по шкале a 0. »змерить рассто€ние от оси до точки удара пули r. ќпыт произвести не менее п€ти раз. –езультаты записать в табл. 1.
“аблица 1
| r, см | ||||||
| α, 0,рад | < α 0> =, рад |
3. ќпределить массу пули, массу грузов, измерить рассто€ние от оси до середины грузов l. –езультаты записать в табл. 2.
¬ключить установку в сеть 220 ¬.
4. »змерить период колебаний ма€тника без грузов “ 0. ƒл€ этого нажать кнопку —еть (на задней панели секундомера), отвести рамку ма€тника на небольшой угол к электромагниту, магнит прит€нет рамку. Ќажать кнопку ѕуск, магнит отпустит рамку. Ќачнетс€ счет времени и числа колебаний. „тобы измерить врем€ дес€ти колебаний t, следует после совершени€ дев€того колебани€ нажать кнопку —топ секундомера. ѕериод равен T 0 =t/ 10. –езультат записать в табл. 2.
5. »змерить период колебаний “ 1 рамки с грузами. ƒл€ этого надеть на рамку добавочные грузы. Ќажать кнопку —брос дл€ обнулени€ индикаторов и включени€ магнита. ќтвести рамку к магниту, нажать ѕуск, измерить врем€ дес€ти колебаний. –езультат записать в табл. 2. ¬ыключить установку.
|
|
|
“аблица 2
| ћасса пули m, г | |
| –ассто€ние до груза l, см | |
| ћасса груза mгр , г | |
| ѕериод без грузов “ 0, с | |
| ѕериод с грузами “ 1, с | |
| ћомент инерции J,кг м2 | |
| ”глова€ скорость <w 0> 1 /с |
6. ѕроизвести расчеты в системе —». ќпределить момент инерции ма€тника по формуле (7). ќпределить среднее значени€ угла поворота <a 0 >. ќпределить среднее значение амплитуды угловой скорости <w 0 > по формуле (8) по среднему значению угла <α 0 >. ќпределить среднее значение скорости <V> по формуле (2). –езультаты записать в табл. 1 и 2.
7. ќценить случайную погрешность измерений скорости пули, полага€, что основной вклад вносит случайна€ погрешность измерени€ угла поворота, по формуле
 , где
, где  . (9)
. (9)
8. «аписать результат работы в виде V = <V> ± d V, P = 0,9. —делать выводы.
ќЌ“–ќЋ№Ќџ≈ ¬ќѕ–ќ—џ
1. ƒайте определение крутильного ма€тника. ¬ыведите и объ€сните формулу дл€ периода колебаний ма€тника.
2. ƒайте определение момента импульса материальной точки, твердого тела. ак определить направление момента импульса тела?
3. —формулируйте закон сохранени€ момента импульса. ѕочему его можно применить дл€ процесса удара пули о мишень ма€тника?
4. «апишите закон сохранени€ момента импульса дл€ удара пули о мишень ма€тника.
5. —делайте вывод формулы дл€ расчета амплитуды угловой скорости ма€тника.
6. ќбъ€сните метод определени€ момента инерции ма€тника с помощью добавочных грузов.
–абота 6






