Дисперсию дискретной случайной величины  вычисляют по формулам:
вычисляют по формулам:
 или
или  .
.
Пусть  -постоянная величина.
-постоянная величина.
Свойства математического ожидания: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  , если
, если  и
и  независимы.
независимы.
Свойства дисперсии: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 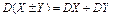 , если
, если  и
и  независимы.
независимы.
Случайная величина  называется непрерывной случайной величиной (НСВ), если её функция распределения представляется в виде
называется непрерывной случайной величиной (НСВ), если её функция распределения представляется в виде  ,
,  , где
, где 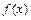 -неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности (распределения) вероятностей. Множество возможных значений непрерывной случайной величины несчётно и обычно представляет собой некоторый конечный или бесконечный промежуток числовой прямой.
-неотрицательная и интегрируемая в бесконечных пределах функция, называемая функцией плотности (распределения) вероятностей. Множество возможных значений непрерывной случайной величины несчётно и обычно представляет собой некоторый конечный или бесконечный промежуток числовой прямой.
Функция распределения 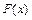 непрерывной случайной величины
непрерывной случайной величины  является непрерывной неубывающей функцией на всей числовой прямой, причём вероятность попадания в любую фиксированную точку равна нулю:
является непрерывной неубывающей функцией на всей числовой прямой, причём вероятность попадания в любую фиксированную точку равна нулю: 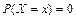 ,
,  .
.
Функция 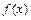 является плотностью вероятностей некоторой НСВ
является плотностью вероятностей некоторой НСВ  , тогда и только тогда, когда: 1)
, тогда и только тогда, когда: 1)  ; 2)
; 2)  .
.
Для непрерывной случайной величины  с плотностью вероятностей
с плотностью вероятностей 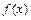 :
: 
 .
.
Математическим ожиданием непрерывной случайной величины  называется число
называется число  , если интеграл сходится абсолютно.
, если интеграл сходится абсолютно.
Дисперсию непрерывной случайной величины  вычисляют по формулам:
вычисляют по формулам:
 или
или  .
.
Медианой непрерывной случайной величины  называется число
называется число  , удовлетворяющее условию
, удовлетворяющее условию  или
или  .
.
Тема 16. Элементы математической статистики. Предварительная обработка статистических данных.
Выборкой объёма  из генеральной совокупности
из генеральной совокупности  называется совокупность
называется совокупность  наблюдаемых значений случайной величины
наблюдаемых значений случайной величины  , соответствующих
, соответствующих  независимым повторениям случайного эксперимента с которым связана величина
независимым повторениям случайного эксперимента с которым связана величина  . В математической статистике генеральную совокупностьотождествляют со случайной величиной, совокупность всех возможных значений которой и называют генеральной совокупностью.
. В математической статистике генеральную совокупностьотождествляют со случайной величиной, совокупность всех возможных значений которой и называют генеральной совокупностью.
Выборка может быть записана в виде вариационного и статистического (дискретного или интервального) рядов. Выборку, записанную в виде статистического ряда, называют группированной.
Вариационным рядом выборки  называется такой способ её записи, при котором элементы выборки упорядочиваются по величине, т.е. записываются в виде последовательности
называется такой способ её записи, при котором элементы выборки упорядочиваются по величине, т.е. записываются в виде последовательности  , где
, где  . Разность
. Разность  называется размахом выборки. Всюду в дальнейшем выборочные характеристики будем, как правило, обозначать символом с «
называется размахом выборки. Всюду в дальнейшем выборочные характеристики будем, как правило, обозначать символом с « » наверху.
» наверху.
Различные значения  ,
,  (
( ), называются вариантами. Число
), называются вариантами. Число  повторений варианты
повторений варианты  в выборке называется её частотой, а отношение
в выборке называется её частотой, а отношение  называется её относительной частотой.
называется её относительной частотой.
Дискретным статистическим рядом называется упорядоченная в порядке возрастания значений вариант  последовательность пар
последовательность пар  ,
,  . Обычно его записывают в виде таблицы, первая стока которой содержит варианты
. Обычно его записывают в виде таблицы, первая стока которой содержит варианты  , а вторая их частоты.
, а вторая их частоты.
Полигоном частот называется фигура, расположенная под ломаной линией с вершинами в точках  , построенных в прямоугольной системе координат.
, построенных в прямоугольной системе координат.
Интервальным статистическим рядом называется последовательность пар  ,
,  , где
, где  - непересекающиеся интервалы, как правило, равной длины, объединением которых является отрезок
- непересекающиеся интервалы, как правило, равной длины, объединением которых является отрезок  , содержащий все выборочные значения;
, содержащий все выборочные значения;  - частота интервала
- частота интервала  , равная числу элементов выборки, значения которых попали в данный интервал. Обычно его записывают в виде таблицы, первая строка которой содержит границы интервалов или их середины
, равная числу элементов выборки, значения которых попали в данный интервал. Обычно его записывают в виде таблицы, первая строка которой содержит границы интервалов или их середины  , а вторая – частоты интервалов.
, а вторая – частоты интервалов.
Гистограммой частот называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах группировки так, что площадь каждого прямоугольника равна частоте  ,
,  . Если длины всех интервалов одинаковы и равны
. Если длины всех интервалов одинаковы и равны  , то высоты прямоугольников равны
, то высоты прямоугольников равны  .
.






