Функция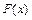 
называется первообразной для функции 
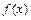на промежутке 
, если 
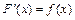для всех 
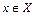. Функция 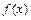может иметь различные первообразные, но все они отличаются друг от друга только постоянными слагаемыми. Поэтому все первообразные для 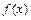содержатся в выражении 
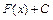, где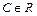 
- произвольная постоянная, которое и называется неопределённым интегралом от функции 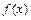и обозначается 
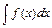. Таким образом, по определению 
.
Операция нахождения первообразной или неопределённого интеграла от функции 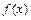называется интегрированием этой функции. Функция 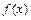для которой на промежутке существует первообразная или неопределённый интеграл называется интегрируемой на этом промежутке. Первообразная и неопределённый интеграл на промежутке существуют у любой непрерывной на этом промежутке функции. Нахождение неопределённого интеграла состоит в таком преобразовании подынтегрального выражения, чтобы получить интегралы из таблицы основных интегралов (приложение 6.3).
Основные свойства неопределённого интеграла:
1.. 2..
3. 
(
).
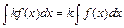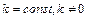4..
5. Если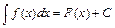 
, то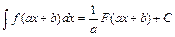 
, 
.
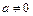Основными методами интегрирования являются: непосредственное интегрирование, интегрирование заменой переменной и по частям.
Непосредственным интегрированием (интегрированием методом разложения) функции 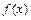называют отыскание неопределённого интеграла 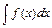с помощью тождественных преобразований подынтегральной функции 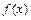, свойств 3-4 неопределённого интеграла и таблицы основных интегралов.
Часто, заменой переменной интегрирования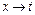 
, удаётся свести нахождение интеграла 
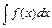к нахождению более простого интеграла 
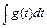с последующей заменой 
.
Очень часто применяют следующий способ замены переменной интегрирования:
,
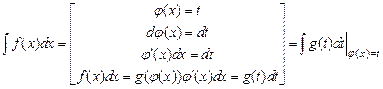где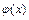 
- некоторая дифференцируемая функция. Функция 
подбирается таким образом, чтобы подынтегральное выражение приняло более удобный для интегрирования вид. Выбор её определяется конкретным видом подынтегрального выражения.
Если 
и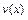 
- дифференцируемые функции, то справедлива формула интегрирования по частям:
или кратко 
.
Эта формула используется в тех случаях для вычисления 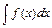, когда подынтегральное выражение 
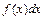можно так представить в виде 
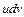, что интеграл 
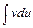может оказаться проще интеграла 
.
Этим методом вычисляются: 1) интегралы вида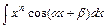 
,
, 
, 
, причём в качестве выбирается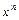 
; 2) интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций: 
, 
, 
, 
, 
, 
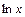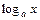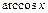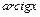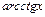, причём в качестве выбирается одна из указанных выше функций. Указанные группы интегралов не исчерпывают всех без исключения интегралов, берущихся методом интегрирования по частям.
Вычисление интегралов вида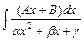 
и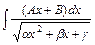 
, выделяя в квадратном трёхчлене 
полный квадрат 
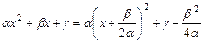и делая замену переменной интегрирования 
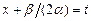, сводят к вычислению табличных интегралов (см. приложение 6.3) и интегралов вида 
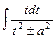и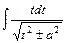 
, которые сводят к табличным заменой переменной 
.
