Решением системы называется всякий упорядоченный набор чисел  , обращающий каждое уравнение системы в равенство. Совокупность всех решений называется множеством решений системы.
, обращающий каждое уравнение системы в равенство. Совокупность всех решений называется множеством решений системы.
Система называется совместной, если она имеет, по крайней мере, одно решение; определённой, если она имеет только одно решение; неопределённой, если она имеет бесконечно много решений; несовместной, если она не имеет решений.
Однородная система уравнений всегда совместна, так как всегда имеет, по крайней мере, нулевое решение  . Треугольная система является определённой, трапециевидная система – неопределённой.
. Треугольная система является определённой, трапециевидная система – неопределённой.
Две системы называются эквивалентными, если множества их решений совпадают.
Элементарными преобразованиями систем уравнений называются:
1) перестановка уравнений;
2) перестановка местами слагаемых  в каждом из уравнений системы;
в каждом из уравнений системы;
3) умножение уравнения на число, отличное от нуля;
4) прибавление к уравнению другого, умноженного на любое число;
5) вычёркивание уравнения вида:  .
.
Основными точными методами решения систем линейных уравнений являются методы: Крамера, обратной матрицы и Гаусса.
Если число уравнений в системе  совпадает с числом неизвестных
совпадает с числом неизвестных  и определитель матрицы системы
и определитель матрицы системы  , то система имеет единственное решение, которое можно найти:
, то система имеет единственное решение, которое можно найти:
а) методом Крамера по формулам:  ,
,  , где
, где  - определитель, получаемый из определителя матрицы системы
- определитель, получаемый из определителя матрицы системы  заменой
заменой 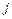 -ого столбца на столбец свободных членов;
-ого столбца на столбец свободных членов;
б ) методом обратной матрицы по формуле  .
.
Методом Гаусса находят решение произвольной системы линейных уравнений. Метод состоит в приведении системы уравнений, с помощью элементарных преобразований, к системе специального вида, эквивалентной исходной, решение которой очевидно. Преобразования по методу Гаусса выполняют в два этапа. Первый этап называют прямым ходом, второй - обратным.
В результате прямого хода выясняют: совместна или нет система и если совместна то, сколько имеет решений - одно или бесконечно много. Преобразования прямого хода выполняют, как правило, над расширенной матрицей системы  , которую получают, приписывая справа к матрице системы
, которую получают, приписывая справа к матрице системы  столбец свободных членов
столбец свободных членов 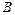 . В результате элементарных преобразований строк и перестановкой столбцов, матрица системы
. В результате элементарных преобразований строк и перестановкой столбцов, матрица системы  должна быть приведена к матрице
должна быть приведена к матрице  треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами  . При этом, система уравнений, матрица которой
. При этом, система уравнений, матрица которой  , является треугольной с диагональными элементами
, является треугольной с диагональными элементами 
 , будет иметь единственное решение; система уравнений, матрица которой
, будет иметь единственное решение; система уравнений, матрица которой  , является трапециевидной с элементами
, является трапециевидной с элементами 
 , будет иметь бесконечно много решений. Если, при выполнении преобразований расширенной матрицы
, будет иметь бесконечно много решений. Если, при выполнении преобразований расширенной матрицы  , в преобразованной матрице
, в преобразованной матрице  появится строка
появится строка 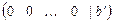 , где
, где  , то это говорит о несовместности исходной системы уравнений.
, то это говорит о несовместности исходной системы уравнений.
В результате обратного хода находят решение системы. Преобразования обратного хода часто выполняют непосредственно над уравнениями системы, соответствующей последней расширенной матрице  прямого хода. В случае единственного решения, его получают, находя последовательно значения всех неизвестных из уравнений системы, начиная с последнего.
прямого хода. В случае единственного решения, его получают, находя последовательно значения всех неизвестных из уравнений системы, начиная с последнего.
Тема 4. Векторы.
Арифметическим вектором называют упорядоченную совокупность из 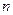 чисел:
чисел:  и обозначают
и обозначают  . Числа
. Числа 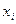 называют компонентами вектора
называют компонентами вектора  , число компонент называют его размерностью.
, число компонент называют его размерностью.
Векторы  и
и  называют равными, если они одинаковой размерности и их соответствующие компоненты равны:
называют равными, если они одинаковой размерности и их соответствующие компоненты равны:  ,
,  .
.
Суммой векторов  и
и  одной размерности, называют вектор
одной размерности, называют вектор  той же размерности, для которого:
той же размерности, для которого:  ,
,  .
.
Произведением вектора  на число
на число 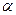 называют вектор
называют вектор 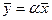 той же размерности, для которого:
той же размерности, для которого:  ,
,  .
.
Множество всех 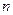 -мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторнымпространством и обозначают
-мерных векторов, в котором введены операции сложения и умножения на число, удовлетворяющие определённым требованиям (аксиомам) называют векторнымпространством и обозначают 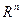 .
.
Скалярным произведением двух арифметических векторов  и
и  называют число:
называют число:
 .
.
Два вектора  и
и  называют ортогональными, если
называют ортогональными, если  .
.
Вектором (геометрическим) называется направленный отрезок, задаваемый упорядоченной парой точек (началом и концом вектора). Обозначают вектор  или
или  . Расстояние между началом и концом вектора называется его длиной и обозначается
. Расстояние между началом и концом вектора называется его длиной и обозначается  или
или  . Углом между векторами
. Углом между векторами  и
и  называется угол
называется угол  ,
,  , на который следует повернуть один из векторов, чтобы его направление совпало с направлением другого вектора, при условии, что их начала совпадают. Проекцией вектора
, на который следует повернуть один из векторов, чтобы его направление совпало с направлением другого вектора, при условии, что их начала совпадают. Проекцией вектора  на вектор
на вектор  называется число
называется число  .
.
Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются компланарными, если они расположены в одной плоскости или в параллельных плоскостях.
Векторы 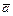 и
и  называются равными и пишут
называются равными и пишут  , если они коллинеарны, одинаково направлены и имеют равные длины. Векторы
, если они коллинеарны, одинаково направлены и имеют равные длины. Векторы 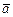 и
и  называются противоположными и пишут
называются противоположными и пишут  , если они коллинеарны, направлены в разные стороны и имеют равные длины.
, если они коллинеарны, направлены в разные стороны и имеют равные длины.
Суммой векторов 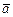 и
и  называется вектор
называется вектор  , соединяющий начало вектора
, соединяющий начало вектора 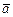 и конец вектора
и конец вектора  , при условии, что конец вектора
, при условии, что конец вектора 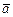 совпадает с началом вектора
совпадает с началом вектора  (правило треугольника). Произведением вектора
(правило треугольника). Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  :
:
1) коллинеарный вектору  ; 2) имеющий длину
; 2) имеющий длину 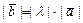 ; 3) направленный одинаково с вектором
; 3) направленный одинаково с вектором  , если
, если  , и противоположно, если
, и противоположно, если  .
.
Ортом вектора  , называется вектор
, называется вектор  , имеющий единичную длину и направление вектора
, имеющий единичную длину и направление вектора  :
:  .
.
Базисом в пространстве  называется упорядоченная тройка некомпланарных векторов, базисом на плоскости
называется упорядоченная тройка некомпланарных векторов, базисом на плоскости  – упорядоченная пара неколлинеарных векторов, базисом на прямой
– упорядоченная пара неколлинеарных векторов, базисом на прямой  – любой ненулевой вектор на этой прямой. Базис, в котором все векторы попарно перпендикулярны и имеют единичную длину, называется ортонормированным. Векторы ортонормированного базиса обозначаются:
– любой ненулевой вектор на этой прямой. Базис, в котором все векторы попарно перпендикулярны и имеют единичную длину, называется ортонормированным. Векторы ортонормированного базиса обозначаются:  и
и 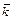 , и называются базисными ортами. Различают правый и левый ортонормированные базисы. Базис
, и называются базисными ортами. Различают правый и левый ортонормированные базисы. Базис  -называется правым, если кратчайший поворот от
-называется правым, если кратчайший поворот от 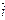 к
к  совершается против хода часовой стрелки, в противном случае он – левый. Базис
совершается против хода часовой стрелки, в противном случае он – левый. Базис  -называется правым, если из конца вектора
-называется правым, если из конца вектора 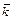 кратчайший поворот от вектора
кратчайший поворот от вектора 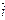 к
к  виден совершающимся против хода часовой стрелки, в противном случае он – левый.
виден совершающимся против хода часовой стрелки, в противном случае он – левый.
Условием коллинеарности векторов  и
и  является равенство:
является равенство:  , где
, где 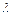 - некоторое число. Условием компланарности векторов
- некоторое число. Условием компланарности векторов  ,
,  и
и 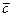 является равенство:
является равенство: 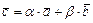 , где
, где  - некоторые числа.
- некоторые числа.
Всякий геометрический вектор может быть разложен единственным образом по векторам базиса, коэффициенты разложения называются при этом координатами вектора в данном базисе. Например, если 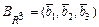 - базис
- базис  и
и  , то всегда существует единственное разложение:
, то всегда существует единственное разложение: 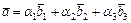 , где числа
, где числа  - координаты вектора
- координаты вектора  в базисе
в базисе  , при этом пишут
, при этом пишут 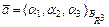 . Если в
. Если в  зафиксирован ортонормированный базис
зафиксирован ортонормированный базис  и
и 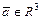 , то равносильны записи:
, то равносильны записи:  и
и 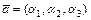 (в записи вектора в координатной форме ортонормированный базис не указывают).
(в записи вектора в координатной форме ортонормированный базис не указывают).
Представление геометрических векторов в координатной форме, позволяет выполнять действия над ними, как над арифметическими векторами:
 ;
;
 .
.
Декартовой прямоугольной системой координатв пространстве называется совокупность точки 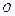 (начало координат) и правого ортонормированного базиса
(начало координат) и правого ортонормированного базиса  и обозначается
и обозначается  . Прямые
. Прямые  ,
,  ,
, 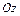 , проходящие через начало координат в направлении базисных векторов, называются координатными осями: первая – осью абсцисс, вторая – осью ординат, третья – осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Аналогично вводится система координат на плоскости:
, проходящие через начало координат в направлении базисных векторов, называются координатными осями: первая – осью абсцисс, вторая – осью ординат, третья – осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Аналогично вводится система координат на плоскости:  .
.
Пусть  - произвольная точка пространства, в котором введена система координат
- произвольная точка пространства, в котором введена система координат  =
=  . Радиус-вектором точки
. Радиус-вектором точки  называется вектор
называется вектор  , который всегда единственным образом можно представить в виде:
, который всегда единственным образом можно представить в виде: 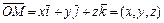 . Числа
. Числа 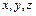 , являющиеся координатами радиус-вектора, совпадают с проекциями вектора
, являющиеся координатами радиус-вектора, совпадают с проекциями вектора  на базисные орты
на базисные орты  и
и 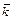 (на координатные оси
(на координатные оси  и
и 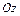 ). Координатами точки
). Координатами точки  в системе координат
в системе координат  называются координаты её радиус-вектора
называются координаты её радиус-вектора  и пишут
и пишут  . В свою очередь, координаты точки
. В свою очередь, координаты точки  полностью определяют её радиус-вектор
полностью определяют её радиус-вектор  . Всякий геометрический вектор
. Всякий геометрический вектор 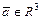 в системе координат
в системе координат  , всегда можно представить как радиус-вектор некоторой точки и записать в виде:
, всегда можно представить как радиус-вектор некоторой точки и записать в виде:  .
.
Длина 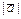 вектора
вектора  , заданного координатами
, заданного координатами  , определяется формулой:
, определяется формулой:  . Направляющими косинусами вектора
. Направляющими косинусами вектора  называются числа:
называются числа:  ,
,  ,
,  , при этом
, при этом  .
.
Координаты вектора  , заданного точками
, заданного точками  и
и  определяются по формуле:
определяются по формуле:  . Расстояние
. Расстояние 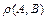 между точками
между точками  и
и  определяется как длина вектора
определяется как длина вектора  и находится по формуле:
и находится по формуле:
 .
.
Координаты точки  делящей отрезок
делящей отрезок  пополам находятся по формулам:
пополам находятся по формулам:  ,
,  ,
,  .
.
Скалярным произведением векторов  и
и  называется число
называется число  . Скалярное произведение обладает свойствами:
. Скалярное произведение обладает свойствами:
1)  ; 2)
; 2)  где
где  - число;
- число;
3)  ; 4)
; 4) 
5)  ; 6)
; 6)  ,
, 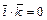 ,
,  ,
, 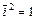 ,
,  ,
,  . Для векторов
. Для векторов  и
и  , заданных своими координатами
, заданных своими координатами  ,
,  скалярное произведение вычисляется по формуле:
скалярное произведение вычисляется по формуле:
 .
.
Скалярное произведение применяют: 1) для вычисления угла между векторами  и
и  по формуле:
по формуле:  ; 2) для вычисления проекции вектора
; 2) для вычисления проекции вектора  на вектор
на вектор  по формуле:
по формуле:  ; 3) в качестве условия перпендикулярности векторов
; 3) в качестве условия перпендикулярности векторов  и
и  :
:  .
.
Векторным произведением векторов 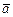 и
и  называется вектор
называется вектор 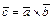 , определяемый условиями: 1)
, определяемый условиями: 1)  ;
;
2)  и
и  ; 3)
; 3)  - правая тройка векторов.
- правая тройка векторов.
Упорядоченная тройка  некомпланарных векторов называется правой тройкой, если из конца третьего вектора
некомпланарных векторов называется правой тройкой, если из конца третьего вектора 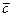 , кратчайший поворот от первого вектора
, кратчайший поворот от первого вектора  ко второму
ко второму  , виден совершающимся против хода часовой стрелки. В противном случае, тройка
, виден совершающимся против хода часовой стрелки. В противном случае, тройка  называется левой.
называется левой.
Векторное произведение обладает свойствами:
1)  ; 2)
; 2) 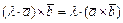 , где
, где  - число;
- число;
3)  ; 4)
; 4)  5)
5)  ;
;
6)  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Для векторов  и
и  , заданных координатами
, заданных координатами  ,
,  векторное произведение вычисляется по формуле:
векторное произведение вычисляется по формуле:
 .
.
Векторное произведение  применяют: 1) для вычисления площадей треугольника и параллелограмма, построенных на векторах
применяют: 1) для вычисления площадей треугольника и параллелограмма, построенных на векторах  и
и  , как на сторонах, по формуле:
, как на сторонах, по формуле:  ; 2) в качестве условия параллельности векторов
; 2) в качестве условия параллельности векторов  и
и  :
:  .
.
Смешанным произведением упорядоченной тройки векторов  ,
,  и
и  называется число
называется число  .
.
Смешанное произведение обладает свойствами:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  и
и 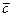 -компланарны
-компланарны  ;
;






