К понятию определённого интеграла можно прийти, решая задачу о вычислении площади криволинейной трапеции, т.е. фигуры, заключённой между прямыми  ,
,  ,
,  и кривой
и кривой  . Число, равное площади криволинейной трапеции, причём площадь той части, которая лежит выше оси
. Число, равное площади криволинейной трапеции, причём площадь той части, которая лежит выше оси  берётся со знаком «+», и ниже её – со знаком «
берётся со знаком «+», и ниже её – со знаком « » и называется определённым интегралом от функции
» и называется определённым интегралом от функции 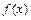 на отрезке
на отрезке  . Определённый интеграл обозначается
. Определённый интеграл обозначается  , где числа
, где числа 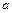 ,
, 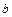 называются нижним и верхним пределами интегрирования.
называются нижним и верхним пределами интегрирования.
Функция  , для которой на отрезке
, для которой на отрезке  существует определённый интеграл, называется интегрируемой на этом отрезке. Достаточным условием интегрируемости функции
существует определённый интеграл, называется интегрируемой на этом отрезке. Достаточным условием интегрируемости функции  на отрезке
на отрезке  является её непрерывность на данном отрезке. Если функция
является её непрерывность на данном отрезке. Если функция 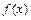 интегрируема на
интегрируема на  , то, по определению, полагают
, то, по определению, полагают  ,
,  .
.
Основные свойства определённого интеграла:
1.. 2..
3..
Понятие определённого интеграла тесно связано с понятием неопределённого интеграла (первообразной).
Если функция 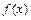 непрерывна на отрезке
непрерывна на отрезке  и
и 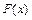 - одна из её первообразных, то справедливо равенство:
- одна из её первообразных, то справедливо равенство:
 (формула Ньютона-Лейбница).
(формула Ньютона-Лейбница).
Следствиями формулы Ньютона-Лейбница являются формулы замены переменной: 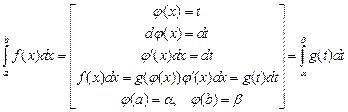 и интегрирования по частям
и интегрирования по частям  в определённом интеграле. При замене переменной в определённом интеграле в отличие от вычисления неопределённого не нужно возвращаться к исходному аргументу, так как преобразованный определённый интеграл берётся по тому отрезку, по которому изменяется новый аргумент.
в определённом интеграле. При замене переменной в определённом интеграле в отличие от вычисления неопределённого не нужно возвращаться к исходному аргументу, так как преобразованный определённый интеграл берётся по тому отрезку, по которому изменяется новый аргумент.
При вычислении неопределённого интеграла по умолчанию предполагалось, что первообразная находится на тех промежутках, на которых выполняемые преобразования подынтегральной функции являются тождественными. При вычислении же определённого интеграла первообразная находится на заданном отрезке, поэтому здесь уже необходимо следить за тождественностью выполняемых преобразований.
Площадь фигуры (рис.1)  ,
,  равна
равна
 .
.
Площадь фигуры (рис.2)  ,
,  равна
равна
 .
.

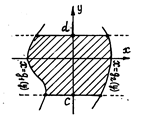
Рис.1 Рис.2
Если функция  интегрируема на отрезке
интегрируема на отрезке  , то несобственным интегралом по бесконечному промежутку интегрирования от функции
, то несобственным интегралом по бесконечному промежутку интегрирования от функции 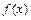 на промежутке
на промежутке  называется
называется  и обозначается
и обозначается  , т.е.
, т.е. 
 . Аналогично:
. Аналогично: 
 .
.
Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Тема 12. Дифференциальные уравнения первого порядка.
Уравнение вида  , где
, где  - искомая функция, называется обыкновенным дифференциальным уравнением первого порядка. Функция
- искомая функция, называется обыкновенным дифференциальным уравнением первого порядка. Функция 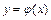 , обращающая уравнение в тождество, называется решением уравнения. Если решение уравнения задано в неявном виде
, обращающая уравнение в тождество, называется решением уравнения. Если решение уравнения задано в неявном виде  , то оно обычно называется интегралом уравнения. Процесс нахождения решений называется интегрированием дифференциального уравнения.
, то оно обычно называется интегралом уравнения. Процесс нахождения решений называется интегрированием дифференциального уравнения.
Уравнение вида  , где
, где  - заданная функция переменных
- заданная функция переменных  и
и  , называется ДУ первого порядка, разрешённым относительно производной. Эту форму записи ДУ называют нормальной. Учитывая, что
, называется ДУ первого порядка, разрешённым относительно производной. Эту форму записи ДУ называют нормальной. Учитывая, что 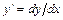 , ДУ первого порядка, разрешённое относительно производной, можно всегда записать в дифференциальной форме:
, ДУ первого порядка, разрешённое относительно производной, можно всегда записать в дифференциальной форме:  , где
, где 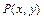 и
и 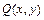 - заданные функции переменных
- заданные функции переменных  и
и  .
.
Условие 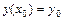 , где
, где  ,
,  -заданные числа, называется начальным условием. Задача нахождения решения уравнения
-заданные числа, называется начальным условием. Задача нахождения решения уравнения  , удовлетворяющего заданному начальному условию
, удовлетворяющего заданному начальному условию 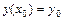 , называется задачей Коши.
, называется задачей Коши.
Общим решением ДУ первого порядка называется решение  , зависящее от одной произвольной постоянной
, зависящее от одной произвольной постоянной  , такое, из которого при надлежащем выборе значения постоянной
, такое, из которого при надлежащем выборе значения постоянной  можно получить решение
можно получить решение  , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию 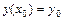 . Общее решение, заданное в неявном виде
. Общее решение, заданное в неявном виде  , называется общим интегралом уравнения.
, называется общим интегралом уравнения.
Частным решением ДУ первого порядка называется решение  , получаемое из общего при конкретном значении постоянной
, получаемое из общего при конкретном значении постоянной  (при этом не исключаются и значения
(при этом не исключаются и значения  ). Частное решение, заданное в неявном виде
). Частное решение, заданное в неявном виде  , называется частным интегралом уравнения.
, называется частным интегралом уравнения.
ДУ вида 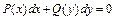 называется уравнением сразделёнными переменными. Его общий интеграл имеет вид
называется уравнением сразделёнными переменными. Его общий интеграл имеет вид  .
.
ДУ вида  или
или  называется уравнением с разделяющимися переменными. Его интегрирование, путём деления обеих частей уравнения на
называется уравнением с разделяющимися переменными. Его интегрирование, путём деления обеих частей уравнения на 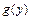 или
или  , сводится (с учётом
, сводится (с учётом 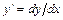 ) к интегрированию уравнения с разделёнными переменными.
) к интегрированию уравнения с разделёнными переменными.
Найти частное решение дифференциального уравнения первого порядка – значит: 1) найти его общее решение  или общий интеграл
или общий интеграл  ; 2) найти то частное решение
; 2) найти то частное решение  (частный интеграл
(частный интеграл  ) которое удовлетворяет заданному начальному условию
) которое удовлетворяет заданному начальному условию 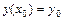 .
.
Дифференциальное уравнение вида  называется однородным.
называется однородным.
Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой 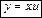 ,
, 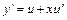 или
или 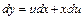 , где
, где 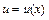 - новая неизвестная функция. Интегрируя ДУ с разделяющимися переменными относительно функции
- новая неизвестная функция. Интегрируя ДУ с разделяющимися переменными относительно функции  и возвращаясь к искомой функции
и возвращаясь к искомой функции 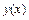 , находим общее решение исходного уравнения. Иногда целесообразно вместо подстановки
, находим общее решение исходного уравнения. Иногда целесообразно вместо подстановки  , использовать подстановку
, использовать подстановку  , где
, где  - новая неизвестная функция.
- новая неизвестная функция.
Уравнение вида  называется линейным. Уравнение
называется линейным. Уравнение  , в котором правая часть тождественно равна нулю, называется однородным линейным уравнением.
, в котором правая часть тождественно равна нулю, называется однородным линейным уравнением.
Общее решение неоднородного линейного уравнения находится подстановкой 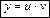 ,
,  , где
, где 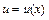 и
и  - неизвестные функции от
- неизвестные функции от  . Уравнение тогда примет вид
. Уравнение тогда примет вид  . Приравняв нулю выражение в скобках, получим уравнение с разделяющимися переменными
. Приравняв нулю выражение в скобках, получим уравнение с разделяющимися переменными  , из которого найдём
, из которого найдём  в виде его частного решения
в виде его частного решения  , где
, где 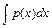 - какая-нибудь первообразная для
- какая-нибудь первообразная для  . Подставив затем найденное выражение
. Подставив затем найденное выражение  в уравнение
в уравнение  , получим уравнение с разделяющимися переменными
, получим уравнение с разделяющимися переменными  , из которого найдём
, из которого найдём 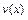 в виде его общего решения. В результате найдём и общее решение исходного уравнения в виде
в виде его общего решения. В результате найдём и общее решение исходного уравнения в виде 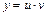 .
.
Уравнение вида  , где
, где  и
и 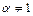 , называется уравнением Бернулли. Решение уравнения Бернулли, также как и линейного, находится подстановкой
, называется уравнением Бернулли. Решение уравнения Бернулли, также как и линейного, находится подстановкой 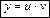 .
.
Тема 13. Дифференциальные уравнения высших порядков.
Уравнение вида  , где
, где  - искомая функция, называется дифференциальным уравнением
- искомая функция, называется дифференциальным уравнением  -го порядка. Функция
-го порядка. Функция 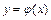 , обращающая уравнение в тождество, называется решением уравнения. Если решение уравнения задано в неявном виде
, обращающая уравнение в тождество, называется решением уравнения. Если решение уравнения задано в неявном виде  , то оно называется интегралом уравнения.
, то оно называется интегралом уравнения.
Уравнение вида  , называется уравнением, разрешённым относительно старшей производной. Эту форму записи ДУ
, называется уравнением, разрешённым относительно старшей производной. Эту форму записи ДУ  -го порядка называют нормальной.
-го порядка называют нормальной.
Условия 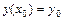 ,
, 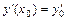 ,…,
,…,  , где
, где  ,
,  ,
,  ,…,
,…,  - заданные числа, называются начальными условиями. Задача нахождения решения уравнения
- заданные числа, называются начальными условиями. Задача нахождения решения уравнения  , удовлетворяющего заданным начальным условиям, называется задачей Коши.
, удовлетворяющего заданным начальным условиям, называется задачей Коши.
Общим решением ДУ  -го порядка называется решение
-го порядка называется решение  , зависящее от
, зависящее от  произвольных постоянных
произвольных постоянных 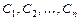 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных 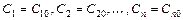 можно получить решение
можно получить решение  , удовлетворяющее заданным начальным условиям
, удовлетворяющее заданным начальным условиям 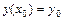 ,
, 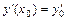 ,…,
,…,  . Общее решение, заданное в неявном виде
. Общее решение, заданное в неявном виде 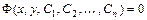 , называется общим интегралом уравнения.
, называется общим интегралом уравнения.
Частным решением ДУ -го порядка называется решение, получаемое из общего при конкретных значениях постоянных. Частное решение, заданное в неявном виде, называется частным интегралом.
Уравнение вида  называется простейшим дифференциальным уравнением
называется простейшим дифференциальным уравнением  -го порядка. Его общее решение находят, выполняя последовательно
-го порядка. Его общее решение находят, выполняя последовательно  интегрирований, и записывают в виде
интегрирований, и записывают в виде
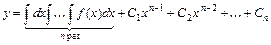 .
.
Функции  ,
,  ,…,
,…,  называются линейно зависимыми на
называются линейно зависимыми на  , если существуют постоянные
, если существуют постоянные  ,
, 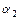 ,…,
,…,  , не все равные нулю, такие, что
, не все равные нулю, такие, что  для всех
для всех  . Если равенство выполняется для всех
. Если равенство выполняется для всех  только при условии
только при условии  , то данные функции называются линейно независимыми на
, то данные функции называются линейно независимыми на  .
.
Уравнение вида  называется линейным дифференциальным уравнением ( ЛДУ )
называется линейным дифференциальным уравнением ( ЛДУ )  -го порядка, где коэффициенты
-го порядка, где коэффициенты 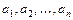 - непрерывные функции или постоянные. Если
- непрерывные функции или постоянные. Если  , то уравнение называется однородным. Однородное линейным уравнение
, то уравнение называется однородным. Однородное линейным уравнение  -го порядка имеет вид
-го порядка имеет вид  .
.
Любая система из  линейно независимых частных решений
линейно независимых частных решений  ,
,  ,…,
,…,  однородного линейного уравнения называется фундаментальной системой его решений.
однородного линейного уравнения называется фундаментальной системой его решений.
Общее решение однородного линейного уравнения  имеет вид
имеет вид  , где
, где 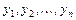 - фундаментальная система его решений;
- фундаментальная система его решений; 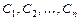 - произвольные постоянные.
- произвольные постоянные.
Фундаментальная система решений 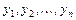 однородного ЛДУ с постоянными коэффициентами
однородного ЛДУ с постоянными коэффициентами  строится на основе характера корней характеристического уравнения
строится на основе характера корней характеристического уравнения  .
.
А именно: 1) если 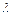 - действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение
- действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение  дифференциального уравнения; 2) если
дифференциального уравнения; 2) если 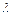 - действительный корень кратности
- действительный корень кратности  , то ему в ФСР соответствует
, то ему в ФСР соответствует  линейно независимых частных решений:
линейно независимых частных решений:  ,
,  ,
,  ,…,
,…,  ; 3) если
; 3) если 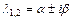 - пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения:
- пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения:  ,
,  .
.
Общее решение неоднородного ЛДУ  имеет вид
имеет вид 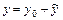 , где
, где  - общее решение соответствующего однородного уравнения,
- общее решение соответствующего однородного уравнения, 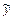 - какое-нибудь частное решение данного неоднородного уравнения.
- какое-нибудь частное решение данного неоднородного уравнения.
Частное решение 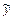 уравнения с правой частью специального вида
уравнения с правой частью специального вида  ищется методом неопределённых коэффициентов в виде
ищется методом неопределённых коэффициентов в виде 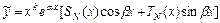 , где
, где  , если число
, если число  не является корнем характеристического уравнения, и
не является корнем характеристического уравнения, и  равно кратности корня
равно кратности корня  в противном случае;
в противном случае;  и
и 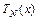 - полные многочлены степени
- полные многочлены степени  с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени
с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени  соответственно являются:
соответственно являются:  ,
,  ,
,  ,
,  ,…. Для нахождения коэффициентов многочленов
,…. Для нахождения коэффициентов многочленов  и
и 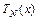 , надо подставить решение
, надо подставить решение 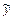 в неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
в неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
Тема 14. Случайные события и их вероятности.
При классическом определении вероятность  случайного события
случайного события  определяется равенством
определяется равенством  , где
, где 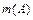 - число элементарных исходов эксперимента (опыта, испытания), благоприятствующих появлению события
- число элементарных исходов эксперимента (опыта, испытания), благоприятствующих появлению события  ;
;  - общее число равновозможных элементарных исходов эксперимента. Каждый из исходов (далее неделимых и взаимно исключающих друг друга) эксперимента называется его элементарным исходом (элементарным событием) и обозначается
- общее число равновозможных элементарных исходов эксперимента. Каждый из исходов (далее неделимых и взаимно исключающих друг друга) эксперимента называется его элементарным исходом (элементарным событием) и обозначается  . Элементарные исходы называются равновозможными, если в силу условий проведения эксперимента можно считать, что ни один из них не является объективно более возможным, чем другие. Множество всех элементарных исходов эксперимента называется пространством элементарных исходов и обозначается
. Элементарные исходы называются равновозможными, если в силу условий проведения эксперимента можно считать, что ни один из них не является объективно более возможным, чем другие. Множество всех элементарных исходов эксперимента называется пространством элементарных исходов и обозначается  . Исход
. Исход  называется благоприятствующим данному событию, если его появление влечёт за собой наступление такого события.
называется благоприятствующим данному событию, если его появление влечёт за собой наступление такого события.
Противоположным событию  называется событие
называется событие 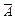 , состоящее в том, что событие
, состоящее в том, что событие  не происходит. Например, противоположным событию, определяемому словами «хотя бы один…» является событие, определяемое словами «ни один…». Если вероятность
не происходит. Например, противоположным событию, определяемому словами «хотя бы один…» является событие, определяемое словами «ни один…». Если вероятность  известна или легко может быть найдена, то вероятность
известна или легко может быть найдена, то вероятность  вычисляют по формуле:
вычисляют по формуле:  .
.
Для вычисления общего числа  элементарных исходов и числа
элементарных исходов и числа 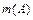 элементарных исходов, благоприятствующих рассматриваемому событию, широко используются правила и формулы комбинаторики. Одной из основных задач комбинаторики является подсчёт числа комбинаторных конфигураций (комбинаций элементов), образованных из элементов некоторых конечных множеств в соответствии с заданными правилами. Примерами таких комбинаций являются перестановки, размещения и сочетания.
элементарных исходов, благоприятствующих рассматриваемому событию, широко используются правила и формулы комбинаторики. Одной из основных задач комбинаторики является подсчёт числа комбинаторных конфигураций (комбинаций элементов), образованных из элементов некоторых конечных множеств в соответствии с заданными правилами. Примерами таких комбинаций являются перестановки, размещения и сочетания.
Сочетаниями из  элементов по
элементов по  называются комбинации элементов, отличающиеся друг от друга только составом элементов. Они рассматриваются как элементарные исходы эксперимента, состоящего в одновременном выборе без возвращения любых
называются комбинации элементов, отличающиеся друг от друга только составом элементов. Они рассматриваются как элементарные исходы эксперимента, состоящего в одновременном выборе без возвращения любых  элементов из
элементов из  различных элементов, а их общее число
различных элементов, а их общее число 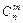 определяется формулой:
определяется формулой:
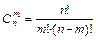 , где
, где  ,
, 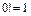 .
.
Размещениями из  элементов по
элементов по  называются комбинации элементов, отличающиеся друг от друга как составом элементов, так и порядком их следования. Они рассматриваются как элементарные исходы эксперимента, состоящего сначала в одновременном выборе без возвращения любых
называются комбинации элементов, отличающиеся друг от друга как составом элементов, так и порядком их следования. Они рассматриваются как элементарные исходы эксперимента, состоящего сначала в одновременном выборе без возвращения любых  элементов из
элементов из  различных элементов, а затем в произвольном их упорядочивании. Общее число
различных элементов, а затем в произвольном их упорядочивании. Общее число  размещений определяется формулой:
размещений определяется формулой:  .
.
Перестановками из  элементов называются комбинации элементов, отличающиеся друг от друга только порядком их следования. Они рассматриваются как элементарные исходы эксперимента, состоящего в произвольном упорядочивании множества, состоящего из
элементов называются комбинации элементов, отличающиеся друг от друга только порядком их следования. Они рассматриваются как элементарные исходы эксперимента, состоящего в произвольном упорядочивании множества, состоящего из  различных элементов, а их общее число
различных элементов, а их общее число  определяется формулой
определяется формулой  .
.
Для подсчёта числа всевозможных комбинаторных конфигураций широко используются правила комбинаторики.
Пусть  - элементы (действия) из некоторого конечного множества элементов (действий), которые можно выбрать (выполнить), соответственно,
- элементы (действия) из некоторого конечного множества элементов (действий), которые можно выбрать (выполнить), соответственно,  способами. Тогда справедливы следующие правила.
способами. Тогда справедливы следующие правила.
Правило сложения. Осуществить выбор (выполнение) только одного из элементов (действий) можно 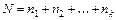 способами.
способами.
Правило умножения. Осуществитьпоследовательный выбор(выполнение) всех элементов (действий) можно  способами.
способами.
Всякое случайное событие  можно рассматривать как подмножество
можно рассматривать как подмножество  (обратное утверждение, вообще говоря, места не имеет), состоящее из всех тех
(обратное утверждение, вообще говоря, места не имеет), состоящее из всех тех  , которые благоприятствуют событию
, которые благоприятствуют событию  (
( ). Множество
). Множество  называют достоверным событием, а пустое множество
называют достоверным событием, а пустое множество  , являющееся по определению подмножеством
, являющееся по определению подмножеством  , называют невозможным событием.
, называют невозможным событием.
Если  , то говорят, что событие
, то говорят, что событие  влечёт событие
влечёт событие 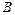 .
.
Произведением событий 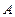 и
и 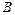 называют событие
называют событие  , происходящее тогда и только тогда, когда происходят одновременно оба события
, происходящее тогда и только тогда, когда происходят одновременно оба события  и
и 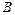 . События
. События 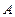 и
и 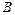 называют несовместными, если
называют несовместными, если 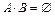 .
.
Суммой событий  и
и 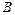 называют событие
называют событие  , происходящее тогда и только тогда, когда происходит хотя бы одно из событий
, происходящее тогда и только тогда, когда происходит хотя бы одно из событий  или
или 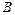 .
.
Разностью событий  и
и 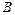 называют событие
называют событие  , происходящее тогда и только тогда, когда происходит событие
, происходящее тогда и только тогда, когда происходит событие  , но не происходит событие
, но не происходит событие 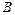 . Событие
. Событие  , происходящее тогда и только тогда, когда событие
, происходящее тогда и только тогда, когда событие  не происходит, называют противоположным событию
не происходит, называют противоположным событию  . Разность событий
. Разность событий  всегда можно представить в виде
всегда можно представить в виде 
 .
.
Из определения вероятности следуют следующие её свойства:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) Если
; 4) Если  , то
, то  ;
;
5)  ; 6)
; 6)  .
.
Пусть  и
и 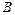 - наблюдаемые события в эксперименте, причём
- наблюдаемые события в эксперименте, причём  . Условной вероятностью
. Условной вероятностью  осуществления события
осуществления события 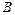 при условии, что событие
при условии, что событие  произошло в результате данного эксперимента, называется величина, определяемая равенством:
произошло в результате данного эксперимента, называется величина, определяемая равенством: 
 .
.
События 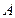 и
и 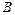 , имеющие ненулевую вероятность, называются независимыми, если выполняется равенство
, имеющие ненулевую вероятность, называются независимыми, если выполняется равенство 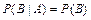 или
или 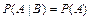 , в противном случае события
, в противном случае события 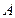 и
и 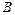 называются зависимыми.
называются зависимыми.
Сложным называют событие, наблюдаемое в эксперименте и выраженное через другие наблюдаемые в том же эксперименте события с помощью допустимых алгебраических операций над событиями.
Вероятность осуществления того или иного сложного события вычисляется с помощью формул умножения вероятностей:
1)  ,
, 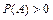 ;
;
2) 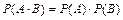 (для независимых событий)
(для независимых событий)
и формул сложения вероятностей:
3) 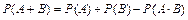 ;
;
4) 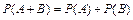 (для несовместных событий).
(для несовместных событий).
Пусть  - наблюдаемые события для данного эксперимента, попарно несовместные (
- наблюдаемые события для данного эксперимента, попарно несовместные ( при
при  ) и образующие полную группу событий (
) и образующие полную группу событий (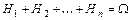 ). Такие события
). Такие события  принято называть гипотезами по отношению к событию
принято называть гипотезами по отношению к событию  . Тогда для любого наблюдаемого в эксперименте события
. Тогда для любого наблюдаемого в эксперименте события  имеет место формула полной вероятности:
имеет место формула полной вероятности:
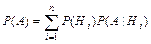 , где
, где  .
.
Пусть  - совокупность гипотез по отношению к событию
- совокупность гипотез по отношению к событию  , безусловные вероятности которых
, безусловные вероятности которых  , называемые априорными (доопытными), известны и пусть стало известно, что в результате эксперимента событие
, называемые априорными (доопытными), известны и пусть стало известно, что в результате эксперимента событие  произошло. Тогда апостериорные (послеопытные) вероятности
произошло. Тогда апостериорные (послеопытные) вероятности  гипотез
гипотез  при условии, что событие
при условии, что событие  имело место, вычисляются по формуле Байеса:
имело место, вычисляются по формуле Байеса:
 , где
, где 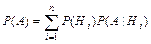 .
.
Формула Байеса позволяет переоценить вероятность каждой из гипотез после поступления дополнительной информации относительно осуществления тех или иных наблюдаемых событий.
Схемой Бернулли называют последовательность испытаний, удовлетворяющую условиям: 1) результатом каждого испытания является один из двух возможных исходов: «успех» (появление некоторого события  ) и «неудача»; 2) испытания являются независимыми, т.е. вероятность «успеха» в каждом следующем испытании не зависит от результатов предыдущих испытаний; 3) вероятность «успеха» во всех испытаниях одинакова и равна
) и «неудача»; 2) испытания являются независимыми, т.е. вероятность «успеха» в каждом следующем испытании не зависит от результатов предыдущих испытаний; 3) вероятность «успеха» во всех испытаниях одинакова и равна 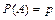 .
.
Вероятность  того, что в
того, что в  испытаниях по схеме Бернулли произойдёт ровно
испытаниях по схеме Бернулли произойдёт ровно  «успехов», определяется формулой Бернулли:
«успехов», определяется формулой Бернулли:
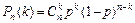 ,
,  .
.
Следствием формулы Бернулли является формула: 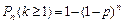 - вероятность того, что в
- вероятность того, что в  испытаниях по схеме Бернулли «успех» наступит хотя бы один раз.
испытаниях по схеме Бернулли «успех» наступит хотя бы один раз.
Тема 15. Случайные величины.
Под случайной величиной  понимают величину, принимающую свои возможные значения
понимают величину, принимающую свои возможные значения  в зависимости от исхода
в зависимости от исхода  эксперимента, с которым она связана.
эксперимента, с которым она связана.
Законом распределения (вероятностей) случайной величины называют любое правило, позволяющее найти вероятность того, что случайная величина примет значение из некоторого подмножества своих возможных значений. Общим законом распределения, присущим всем случайным величинам, является функция распределения.
Функцией распределения (вероятностей) случайной величины  называется функция
называется функция 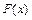 действительной переменной
действительной переменной  ,
,  , определяемая формулой
, определяемая формулой  .
.
Каждая функция распределения 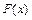 обладает следующими свойствами:
обладает следующими свойствами:
1)  ,
,  ; 2)
; 2) 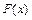 не убывает;
не убывает;
3)  ,
,  ; 4)
; 4) 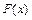 непрерывна слева.
непрерывна слева.
Вероятность события  определяется формулой:
определяется формулой:
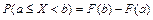 .
.
Случайная величина  называется дискретной случайной величиной (ДСВ), если множество её возможных значений
называется дискретной случайной величиной (ДСВ), если множество её возможных значений  конечно или счётно, причём
конечно или счётно, причём  ,
,  , где суммирование распространяется на все возможные значения
, где суммирование распространяется на все возможные значения  .
.
Закон распределения ДСВ удобно задавать рядом распределения. Рядом распределения ДСВ называют таблицу, в которой перечислены все возможные значения  этой случайной величины и соответствующие им вероятности
этой случайной величины и соответствующие им вероятности  . Для наглядности закон распределения ДСВ изображают графически, для чего в прямоугольной системе координат строят точки
. Для наглядности закон распределения ДСВ изображают графически, для чего в прямоугольной системе координат строят точки 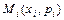 и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Математическим ожиданием дискретной случайной величины  называется число
называется число  , если ряд сходится абсолютно.
, если ряд сходится абсолютно.






