Який геометричний зміст має визначений інтеграл  , якщо f(x)>0? , якщо f(x)>0?
| це є кут нахилу дотичної до осі 0х
| це є довжина відрізка в межах інтегрування
| *це є площа відповідної криволінійної трапеції
| це є площа кола, діаметр якого дорівнює відрізку(a,b)
|
| Вкажіть, чому дорівнює визначений інтеграл з однаковими межами інтегрування?
| *нулю
| одиниці
| мінус одиниці
| нескінченності
|
| Чи зміниться визначений інтеграл, якщо поміняти межі інтегрування?
| не зміниться
| *змінить лише свій знак на протилежний
| зміниться
| зміниться лише величина інтеграла
|
| Нехай f(x)>0 і інтегрована на [ а,b], b > а, то:
|  =0 =0
|  <0 <0
| *  >0 >0
|  = = 
|
| Яка з наведених формул є формулою Ньютона - Лейбніца?
|  = F(a)-F(b) = F(a)-F(b)
|  = F(b) = F(b)
| * 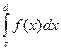 = F(d)-F(c) = F(d)-F(c)
|  = F(а) = F(а)
|
| Яка з наведених формул справедлива для не власного інтеграла?
| * 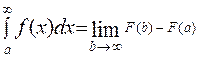
|  = =  F(b)-F(a) F(b)-F(a)
|  = =  + + 
|  = F(b)-F(a) = F(b)-F(a)
|
| Якою буде вірна відповідь для твердження: визначений інтеграл від неперервної функції дорівнює:
| *різниці значень будь-якої первісної для верхньої та нижньої межі інтегрування
| сумі значень первісної для нижньої та верхньої меж інтегрування
| будь-якої первісної по верхній межі інтегрування
| будь-якої первісної по нижній межі інтегрування
|
| Інтеграл з рівними межами інтегрування дорівнює:
| *нулю
|
| -1
| ∞
|
| Як поведе себе визначений інтеграл, якщо поміняти межі інтегрування:
| величина інтеграла не зміниться
| величина інтеграла зміниться
| *величина інтеграла не зміниться, а знак зміниться на протележний
| величина інтеграла зміниться, а знак поміняється на обернений
|
| Функція, для якої на проміжку [а,b] існує визначений інтеграл, називається:
| диференційованою на цьому проміжку
| елементарною
| *інтегрованою на цьому проміжку
| складною функцією
|
| Зміст визначеного інтеграла геометрично полягає в тому, що якщо f(x) ≥0, то він дорівнює:
| тангенсу кута нахилу дотичної до осі 0х
| довжині відрізка в межах інтегрування по осі 0х
| *площі відповідної криволінійної трапеції
| половині площі відповідної криволінійної трапеції
|
| Якщо f(x)>0 і інтегрована на [ а,b], b > а, то:
|  =0 =0
|  <0 <0
| *  >0 >0
|  = = 
|
| Якщо неперервні функції f(х) і φ(х) на проміжку [а, b]справджують нерівність f(х) < φ(х) то:
| 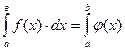
| * 
| 
| 
|
Інтеграл  дорівнює: дорівнює:
| *0
|
| 2
| а
|
Інтеграл  з геометричної точки зору означає: з геометричної точки зору означає:
| відрізок одиничної довжини
| круг, площа якого дорівнює 2
| прямокутник, площа якого дорівнює 2
| *прямокутний трикутник, площа якого дорівнює 2
|
Визначний інтеграл  є є
| сукупність функцій
| * певне число
| множина дійсних чисел
| множина натуральних чисел
|
| Який геометричний зміст має визначений інтеграл?
| кут нахилу дотичної до осі 
| відстань від початку координат до заданої точки
| довжина відрізка в межах інтегрування
| *площа відповідної криволінійної трапеції
|
Якщо 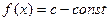 , то чому дорівнює інтеграл , то чому дорівнює інтеграл 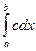
| 
| 
| * 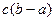
| 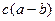
|
Вкажіть правильну відповідь для інтеграла 
| 
| * 
| 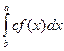
| 
|
Де знаходиться точка с для такого запису 
| a>c>c
| a>c
| c>b
| * a<c<b
|
Якщо  - неперервна для - неперервна для  і b>a, то знайдеться така точка і b>a, то знайдеться така точка 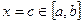 , що: , що:
| * 
| 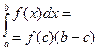
| 
| 
|
Обчисліть інтеграл 
| -1
|
| *0
| 
|
Якщо  >0 і інтегрована для >0 і інтегрована для  а також а також 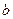 > >  то то  буде буде
|
| <0
|
| *>0
|
Якщо  і і  інтегровані для інтегровані для 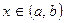 але але  > >  , то: , то:
| *  > > 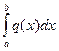
|  < < 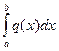
|  = = 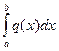
|  + + 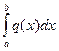 =0 =0
|
Якщо функції 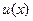 і і  мають неперервні похідні для мають неперервні похідні для  то то  дорівнює дорівнює
| 
| 
| 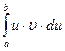
| * 
|
Інтеграл Діріхле  буде збіжним, якщо: буде збіжним, якщо:
| р = 0
| р = 1
| р < 1
| *р > 1
|
Інтеграл Діріхле  буде розбіжним, якщо: буде розбіжним, якщо:
| *р 
| р > 1
| р = 2
| р = 5
|
Невласний інтеграл  обчислюється за формулою: обчислюється за формулою:
| 
| 
| * 
| 
|
Невласний інтеграл  обчислюється за формулою: обчислюється за формулою:
| 
| 
| 
| * 
|
 , якщо f(x)>0?
, якщо f(x)>0?
 =0
=0
 <0
<0
 >0
>0
 =
= 
 = F(a)-F(b)
= F(a)-F(b)
 = F(b)
= F(b)
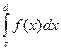 = F(d)-F(c)
= F(d)-F(c)
 = F(а)
= F(а)
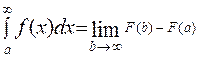
 =
=  F(b)-F(a)
F(b)-F(a)
 =
=  +
+ 
 = F(b)-F(a)
= F(b)-F(a)
 =0
=0
 <0
<0
 >0
>0
 =
= 
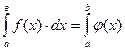



 дорівнює:
дорівнює:
 з геометричної точки зору означає:
з геометричної точки зору означає:
 є
є

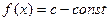 , то чому дорівнює інтеграл
, то чому дорівнює інтеграл 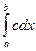


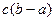
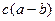



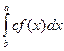


 - неперервна для
- неперервна для  і b>a, то знайдеться така точка
і b>a, то знайдеться така точка 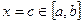 , що:
, що:

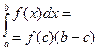




 >0 і інтегрована для
>0 і інтегрована для  а також
а також 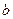 >
>  то
то  буде
буде
 і
і  інтегровані для
інтегровані для 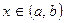 але
але  >
>  , то:
, то:
 >
> 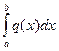
 <
< 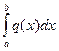
 =
= 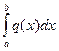
 +
+ 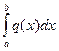 =0
=0
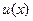 і
і  мають неперервні похідні для
мають неперервні похідні для  то
то  дорівнює
дорівнює


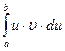

 буде збіжним, якщо:
буде збіжним, якщо:
 буде розбіжним, якщо:
буде розбіжним, якщо:

 обчислюється за формулою:
обчислюється за формулою:




 обчислюється за формулою:
обчислюється за формулою:








