| Диференційована функція зростає на деякому проміжку, якщо:
| похідна цієї функції від’ємна на цьому проміжку
| *похідна додатна на цьому проміжку
| похідна дорівнює нулю
| похідна дорівнює 1
|
| Диференційована функція y=f(x) спадає на деякому проміжку, якщо:
| похідна
| похідна
| *похідна цієї функції від’ємна на цьому проміжку
| похідна цієї функції y'>0 на цьому проміжку
|
| Критичними точками для заданої функції y=f(x) називають ті значення аргументу х, які:
| *перетворюють похідну функції на нуль
| які перетворюють функцію на нескінченність
| в яких похідна від’ємна
| в яких похідна функції дорівнює одиниці
|
| Функція може мати екстремум тільки в тих точках, де похідна:
| y'<0
| y'>0
| *y'=0
| y'=1
|
| Для функції y=f(x) y'(x0)=0, a y''(x0)>0. Що це означає?
| функція f(x0) має максимум
| * f(x0) має мінімум
| f(x0) не має точки екстремуму
| функція f(x0) не визначена в точці х0
|
| Для функції y=f(x) y'(x0)=0, a y''(x0)<0. Що це означає?
| *функція f(x0) має максимум
| функція f(x0) має мінімум
| функція f(x0) не має точки екстремуму
| функція f(x0) невизначена в точці х0
|
| Добуток похідної функції на приріст аргументу y'(x)∆x називається:
| приростом функції ∆y
| приростом аргументу
| *диференціалом функції
| диференціалом аргументу
|
| y=f(x) єнеперервна і диференційована на проміжку (а,b) функція.Щоб функція була сталою на проміжку[а, b] необхідно і достатньо аби:
| 
| 
| 
| * 
|
| Функція Z=f(x,y) має в точці (x0,y0) екстремум. Це означає, що в цій точці:
| 
| 
| 
| * 
|
| Якщо диференційована функція зростає на деякому проміжку, то:
| похідна цієї функції від’ємна на цьому проміжку
| *похідна додатна на цьому проміжку
| похідна дорівнює нулю
| похідна дорівнює 1
|
| Якщо диференційована функція y=f(x) спадає на деякому проміжку, то:
| похідна y'=0
| похідна y'=1
| *похідна цієї функції від’ємна на цьому проміжку
| похідна цієї функції y'>0 на цьому проміжку
|
| Неперервна функція може мати екстремум тільки в тих точках, де похідна:
| y'<0
| y'>0
| *y'=0
| y'=1
|
Якщо  , то функція називається , то функція називається
| обмеженою в точці  ; ;
| *неперервною в точці  ; ;
| диференційовною в точці  ; ;
| розривною в точці  . .
|
| Однією з основних формул для наближених обчислень є формула
| * 
| 
| 
| 
|
Якщо похідна функції  на відрізку на відрізку  додатна, то функція на цьому відрізку додатна, то функція на цьому відрізку
| спадна
| *зростаюча
| не зростаюча
| не спадна
|
Якщо точка  є точкою екстремуму функції є точкою екстремуму функції  , то її похідна в цій точці , то її похідна в цій точці
| *дорівнює 0 або не існує;
| додатна
| від’ємна
| інша відповідь.
|
Якщо точка  є точкою мінімуму функції є точкою мінімуму функції  , то похідна , то похідна  при переході через цю точку при переході через цю точку
| від’ємна в околі т.  ; ;
| змінює знак з (+) на (-);
| додатна в околі т.  ; ;
| *змінює знак з (-) на (+)
|
Якщо точка  є точкою максимуму функції є точкою максимуму функції  , то друга похідна , то друга похідна  : :
| додатна
| *від’ємна
| рівна нулю
| не існує
|
Кажуть, що графік функції  має в інтервалі має в інтервалі  опуклість, напрямлену вниз, якщо опуклість, напрямлену вниз, якщо
| * всі точки графіка функції лежать вище будь-якої своєї дотичної;
| всі точки графіка функції лежать нижче будь-якої своєї дотичної
|  для всіх точок інтервалу для всіх точок інтервалу
|  принаймні в одній точці інтервалу принаймні в одній точці інтервалу
|
Привило Лопіталя для двох диференційованих функцій  та та  записують у вигляді: записують у вигляді:
| 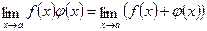
| *  
| 
| 
|
| Необхідна ознака зростання диференційованої функції записується:
| 
|  = 1 = 1
|  < 0 < 0
| *  ≥ 0 ≥ 0
|
Для того, щоб функція  була вгнута на була вгнута на  , достатньо на цьому інтервалі: , достатньо на цьому інтервалі:
| *  > 0 > 0
|  < 0 < 0
|  = -2 = -2
|  = -1 = -1
|
Для того, щоб функція  була на була на  опукла, достатньо щоб на цьому інтервалі: опукла, достатньо щоб на цьому інтервалі:
| *  < 0 < 0
|  > 0 > 0
|  = 1 = 1
|  = 1.5 = 1.5
|
Точка с називається точкою перегину кривої  , ,  , якщо при переході через цю точку її друга похідна: , якщо при переході через цю точку її друга похідна:
| Не змінює свого знаку
| *Змінює знак на протилежний
| Залишається додатною
| Залишається від'ємною
|










 , то функція називається
, то функція називається
 ;
;
 ;
;
 ;
;
 .
.




 на відрізку
на відрізку  додатна, то функція на цьому відрізку
додатна, то функція на цьому відрізку
 є точкою екстремуму функції
є точкою екстремуму функції  , то її похідна в цій точці
, то її похідна в цій точці
 є точкою мінімуму функції
є точкою мінімуму функції  , то похідна
, то похідна  при переході через цю точку
при переході через цю точку
 ;
;
 ;
;
 є точкою максимуму функції
є точкою максимуму функції  , то друга похідна
, то друга похідна  :
:
 має в інтервалі
має в інтервалі  опуклість, напрямлену вниз, якщо
опуклість, напрямлену вниз, якщо
 для всіх точок інтервалу
для всіх точок інтервалу
 принаймні в одній точці інтервалу
принаймні в одній точці інтервалу
 та
та  записують у вигляді:
записують у вигляді:
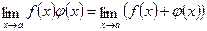





 = 1
= 1
 < 0
< 0
 ≥ 0
≥ 0
 була вгнута на
була вгнута на  , достатньо на цьому інтервалі:
, достатньо на цьому інтервалі:
 > 0
> 0
 < 0
< 0
 = -2
= -2
 = -1
= -1
 була на
була на  опукла, достатньо щоб на цьому інтервалі:
опукла, достатньо щоб на цьому інтервалі:
 < 0
< 0
 > 0
> 0
 = 1
= 1
 = 1.5
= 1.5
 ,
,  , якщо при переході через цю точку її друга похідна:
, якщо при переході через цю точку її друга похідна:






