| Похідною функції y=f(x) за аргументом x називається:
| відношення аргументу до функції, коли остання прямує до нуля
| відношення приросту функції до приросту аргументу
| границя відношення функції до аргументу, коли останній прямує до нуля
| *границя відношення приросту функції до приросту аргументу, коли останній прямує до нуля
|
| Знаходження похідної функції y=f(x) називається:
| *диференціюванням цієї функції
| інтегруванням цієї функції
| відшукання границі функції y=f(x)
| Диференціалом цієї функції
|
| Механічний зміст похідної є:
| середня швидкість зміни функції
| мінімальна швидкість зміни функції в точці
| максимальна швидкість зміни функції в точці
| *миттєва швидкість зміни функції в точці
|
| Функція y=f(x) називається диференційованою в точці функцією, якщо:
| функція в цій точці дорівнює нулю
| якщо похідна в цій точці не існує
| *якщо функція в цій точці має похідну
| якщо функція не має похідну в цій точці
|
| Похідна сталої величини С дорівнює:
| С
| *0
|
| -1
|
| Необхідною умовою диференційованості функції y=f(x) у точці є:
| *її неперервність в цій точці
| рівність нулю похідної в цій точці
| ця точка є точкою розриву функції
| немає вірної відповіді
|
| Похідна алгебраїчної суми двох функцій (u(x) ± v(x))' дорівнює:
| u'(x) + v'(x)
| u'(x) - v'(x)
| u'(x) v'(x)
| *u'(x) ± v'(x)
|
| Похідна добутку двох диференційованих функцій (u(x) *v(x))' дорівнює:
| u'(x) v'(x)
| u'(x) v(x) − v'(x) u(x)
| *u'(x) v(x) + v'(x) u(x)
| v'(x) v(x) + u'(x) u(x)
|
Похідна  , де c-const дорівнює: , де c-const дорівнює:
| cu
| *cu'
|
|
|
| Нехай y=f(u) та u=f(x) диференційовані функції від своїх аргументів, то похідна yx' дорівнює:
| *fu'ux'
| fx ux'
| f(u)  x' x'
| f(x)  (x) (x)
|
| Похідна x'y оберненої функції x=f(y) по змінної у дорівнює:
| x'y= y'x
| *x'y=1/ y'x
| x'y= x'x
| x'y= y'y
|
| Диференціал функції y=f(x) записують:
| dy=y':dx
| dy=x'y'
| dy= 
| *dy=y' x x
|
Область визначення функції  є: є:
| 
| 
| 
| *визначена скрізь, крім х=0
|
| Для функції виконуються умова f(-x)=-f(x),тому функція називається:
| парною 
| *непарною
| періодичною 
| елементарною
|
| Для функції виконується умова f(-x)=f(x), тому функція (x) називається:
| *парною
| непарною
| періодичною
| неперіодичною
|
| Чому дорівнює похідна (cu)', де c-const?
| cu
| *cu'
|
|
|
| Якщо y=f(u) та u=f(x) диференційовані функції від своїх аргументів, то похідна yx' дорівнює:
| *fu'* ux'
| fx'* ux'
| f(u)*  x' x'
| f(x)*  (x) (x)
|
| Похідна x'y оберненої функції x=f(y) по змінної у дорівнює:
| x'y= y'x
| *x'y=1/ y'x
| x'y= x'x
| x'y= y'y
|
| Диференціалом функції у=f(х) називається величина:
| f(x)*Δx
| *f '(x)·Δx
| 
| 
|
| Знайти другий диференціал функції у= х6 - 4х3.
| d2 y=(6x5 – 12x2 )dx2
| * d2 y=(30x4 – 24x)dx2
| d2 y=0
| d2 y=1
|
| Знайти похідну функції у = esin x в точці х=0.
| y' =0
| *y' =1
| y' =-1
| y' =2
|
| Знайти похідну функції у=sіп2х в точці х=0.
| y' =1
| *y' =2
| y' =0
| y' =3
|
Знайти похідну функції   в точці х=2 в точці х=2
| y' = 0
| y' =1
| *y' = 2
| y' = 3
|
| Знайти похідну функції у =sin2 x
| y' = 2sin x
| y' = 2cos x
| * y' = sin 2x
| y' = cos 2x
|
| Якщо функції у=f(х) і у=q(х) неперервні на інтервалі (а, в), то якою буде функція у=f(х)*q(х)?
| *неперервною
| розривною
| неперервною за межами інтервалу
| Не перервною тільки в точці х=а або х=в
|
Для функції виконується умова  , тому функція , тому функція  називається: називається:
| *парною
| непарною
| періодичною
| елементарною
|
Для функції виконується умова  , тому функція , тому функція  називається: називається:
| парною
| *непарною
| періодичною
| елементарною
|
Функція  має область визначення: має область визначення:
| 
| 
| * 
| 
|
Визначити, парна, чи непарна функція  : :
| Функція є парна
| Функція є непарна
| *Функція не є ні парною, ні непарною
| інша відповідь
|
Якщо відношення  має границю при має границю при  , то ця границя називається , то ця границя називається
| *похідною функції  в точці в точці  ; ;
| односторонньою похідною функції  в точці в точці 
| приростом функції  в точці в точці  ; ;
| диференціалом функції  в точці в точці  . .
|
| Якщо функція диференційована в деякій точці, то вона
| має в точці другу похідну
| зростає в деякому околі даної точки
| спадає в деякому околі даної точки
| *неперервна в цій точці
|
Якщо функція  (х) диференційована в точці (х) диференційована в точці  , то , то  дорівнює дорівнює
| кутовому коефіцієнту нормалі до графіка цієї функції в точці 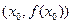
| *кутовому коефіцієнту дотичної до графіка цієї функції в точці 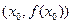
| приросту функції в точці  ; ;
| кутовому коефіцієнту дотичної до графіка функції  в точці в точці 
|
Диференціал функції  у точці у точці  визначається за формулою визначається за формулою
| * 
| 
| 
| 
|
Похідна функції  визначається за формулою визначається за формулою
| 
| 
| * 
| 
|
Якщо  для всіх для всіх  , то графік функції має в інтервалі , то графік функції має в інтервалі 
| графік паралельний осі Ох;
| опуклість, напрямлену вгору
| максимум в одній із точок інтервалу
| *опуклість, напрямлену вниз
|
Якщо   або або  не існує і друга похідна не існує і друга похідна  змінює знак при переході через точку змінює знак при переході через точку  , то точка , то точка 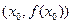 є є
| *точкою перегину
| точкою мінімуму
| точкою максимуму
| критичною точкою.
|
Функція  неперервна на проміжку неперервна на проміжку  якщо вона: якщо вона:
| *Неперервна в кожній точці проміжку 
| Неперервна в точці 
| Неперервна в точці 
| Неперервна в точках  і і 
|
Функція  називається неперервною в точці називається неперервною в точці  справа, якщо: справа, якщо:
| 
| 
| * 
| 
|
| Всі елементарні функції неперервні в інтервалах:
| від 1 до 0
| від 0 до + 
| від -  до + до + 
| *Своєї визначеності
|
Якщо функція  має похідну в кожній точці деякого проміжку, то її називають: має похідну в кожній точці деякого проміжку, то її називають:
| Зростаючою в цьому проміжку
| Інтегрованою на цьому проміжку
| *Диференційованою в цьому проміжку
| Спадною в цьому проміжку
|
Якщо функція  диференційована в деякій точці диференційована в деякій точці  , то вона: , то вона:
| *Неперервна в 
| має розрив в  першого ряду першого ряду
| Має розрив в точці 
| Інтегрована в точці 
|
Геометрично похідна функції  означає: означає:
| Середню швидкість зміни функції
| *Кутовий коефіцієнт дотичної до графіка функції
| Значення кута нахилу функції до осі 
| Площу трикутника
|
В точках розриву функція  : :
| Має похідні
| *Немає похідних
| Має тільки одну похідну
| Має безліч похідних
|
| 155. Похідна функції дорівнює:
| * 
| 
| 
| 
|
Чому дорівнює похідна функції:  (а>0;а≠1) (а>0;а≠1)
| 
| * 
| 
| 
|
Чому дорівнює похідна функції 
| 
| 
| 
| * 
|
Чому дорівнює похідна показникової функції  ? ?
| 
| * 
| 
| 
|
159. Назвіть похідну функції 
| 
| 
| * 
| 
|
Назвіть похідну функції 
| 
| * 
| 
| 
|
Назвіть похідну функції 
| * 
| 
| 
| 
|
Назвіть похідну функції 
| 
| * 
| 
| 
|
Якщо  та та  диференційовані функції від диференційовані функції від  , то чому дорівнює , то чому дорівнює  ? ?
| * 
| 
| 
| 
|
Якщо  та та  диференційовані функції у точках в яких диференційовані функції у точках в яких   , то чому дорівнює , то чому дорівнює 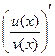 ? ?
| * 
| 
| 
| 
|
Назвіть похідну функції 
| * 
| 
| 
| 
|
Назвіть похідну функції 
| 
| * 
| 
| 
|
Чому дорівнює похідна складної функції  ? ?
| 
| 
| 
| * 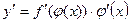
|
Чому дорівнює похідна функції 
| * 
| 
| 
| 
|
Еластичність функції  визначається формулою визначається формулою
| 
| 
| * 
| 
|
Еластичність степеневої функції  дорівнює: дорівнює:
| 
| * 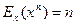
| 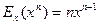
| 
|
Еластичність  показникової функції показникової функції  дорівнює: дорівнює:
| 
| 
| * 
| 
|
Еластичність лінійної функції  дорівнює: дорівнює:
| 
| 
| 
| * 
|
Похідна функції  дорівнює: дорівнює:
| 
| * 
| 
| 
|
| Диференціалом функції називається величина:
| 
| 
| 
| * 
|
Нехай  . Чому дорівнює диференціал . Чому дорівнює диференціал  ? ?
| * 
| 
| 
| 
|
Диференціал сталої величини  дорівнює: дорівнює:
|
| -1
| *0
| 
|
Диференціал  дорівнює: дорівнює:
|
|
| * 
| 
|
Диференціал  дорівнює: дорівнює:
| 
| * 
| 
| 
|
Диференціал  дорівнює: дорівнює:
| * 
| 
| 
| 
|
Диференціал функції  дорівнює: дорівнює:
| 
| 
| * 
| 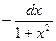
|
Диференціал другого порядку від функції  записують: записують:
| 
| 
| 
| * 
|
Нехай функція  неперервна на неперервна на  , диференційована на , диференційована на  і і  . Чому дорівнює похідна функції в точці . Чому дорівнює похідна функції в точці  , якщо (а< , якщо (а<  < b)? < b)?
|
| *0
| -1
| не існує
|
Нехай функція  неперервна на неперервна на  , диференційована на , диференційована на  і точка і точка  лежить в середині інтервалу, тобто (а< лежить в середині інтервалу, тобто (а<  < b). Чому дорівнює похідна в цій точці < b). Чому дорівнює похідна в цій точці  ? ?
| 
| 
| 
| * 
|
 , де c-const дорівнює:
, де c-const дорівнює:
 x'
x'
 (x)
(x)

 x
x
 є:
є:





 x'
x'
 (x)
(x)



 в точці х=2
в точці х=2
 , тому функція
, тому функція  називається:
називається:
 , тому функція
, тому функція  називається:
називається:
 має область визначення:
має область визначення:




 :
:
 має границю при
має границю при  , то ця границя називається
, то ця границя називається
 в точці
в точці  ;
;
 в точці
в точці 
 в точці
в точці  ;
;
 в точці
в точці  .
.
 (х) диференційована в точці
(х) диференційована в точці  , то
, то  дорівнює
дорівнює
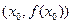
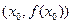
 ;
;
 в точці
в точці 
 у точці
у точці  визначається за формулою
визначається за формулою




 визначається за формулою
визначається за формулою




 для всіх
для всіх  , то графік функції має в інтервалі
, то графік функції має в інтервалі 

 або
або  не існує і друга похідна
не існує і друга похідна  змінює знак при переході через точку
змінює знак при переході через точку  , то точка
, то точка 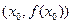 є
є
 неперервна на проміжку
неперервна на проміжку  якщо вона:
якщо вона:



 і
і 
 називається неперервною в точці
називається неперервною в точці  справа, якщо:
справа, якщо:





 до +
до + 
 має похідну в кожній точці деякого проміжку, то її називають:
має похідну в кожній точці деякого проміжку, то її називають:
 диференційована в деякій точці
диференційована в деякій точці  , то вона:
, то вона:

 першого ряду
першого ряду


 означає:
означає:

 :
:




 (а>0;а≠1)
(а>0;а≠1)









 ?
?
























 та
та  диференційовані функції від
диференційовані функції від  , то чому дорівнює
, то чому дорівнює  ?
?




 та
та  диференційовані функції у точках в яких
диференційовані функції у точках в яких 
 , то чому дорівнює
, то чому дорівнює 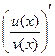 ?
?














 ?
?



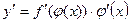





 визначається формулою
визначається формулою




 дорівнює:
дорівнює:

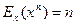
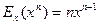

 показникової функції
показникової функції  дорівнює:
дорівнює:




 дорівнює:
дорівнює:




 дорівнює:
дорівнює:








 . Чому дорівнює диференціал
. Чому дорівнює диференціал  ?
?




 дорівнює:
дорівнює:

 дорівнює:
дорівнює:


 дорівнює:
дорівнює:




 дорівнює:
дорівнює:




 дорівнює:
дорівнює:



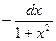
 записують:
записують:




 неперервна на
неперервна на  , диференційована на
, диференційована на  і
і  . Чому дорівнює похідна функції в точці
. Чому дорівнює похідна функції в точці  , якщо (а<
, якщо (а<  < b)?
< b)?
 неперервна на
неперервна на  , диференційована на
, диференційована на  і точка
і точка  лежить в середині інтервалу, тобто (а<
лежить в середині інтервалу, тобто (а<  < b). Чому дорівнює похідна в цій точці
< b). Чому дорівнює похідна в цій точці  ?
?










