Тема 2. Основы линейной алгебры

Элементы содердания	Требования к знаниям и умениям
Умножение матриц	знать: правила выполнения операций над матрицами уметь: выполнять операции над матрицами
Определители третьего порядка	знать: правило вычисления определителей третьего порядка уметь: вычислять определители третьего порядка
Правило Крамера	знать: метод решения систем линейных уравнений по правилу Крамера уметь: решать системы линейных уравнений по правилу Крамера
Действия над матрицами	знать: правила выполнения операций над матрицами уметь: применять правила выполнения операций над матрицами при решении задач
Определители второго порядка	знать: правило вычисления определителя второго порядка уметь: применять правило вычисления определителя второго порядка при решении задач
Системы линейных уравнений	знать: методы решения систем линейных уравнений уметь: решать системы линейных уравнений

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

А =

 

 

Действия с матрицами

1) Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

2) По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.

3) Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

,

то произведением матрицA и B, называется матрица

,

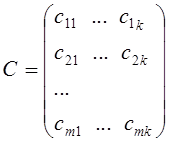элементы которой вычисляются по формуле

c_ij = a _i1 b _1j + a _i2 b _2j +... + a _in b_nj, i = 1, ..., m, j = 1,..., k.

Произведение матриц A и B обозначается AB, т. е. C = AB.

Пусть даны матрицы и .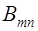

· =

Получаем матрицу С, каждый элемент которой равен сумме произведений элементов i -ой строки матрицы А на соотв. элемент j -го столбца матрицы В.

Произведение А · В определено, если s= m (число столбцов А равно числу строк В). Если 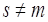, то произведение А · В найти нельзя.

 

Определители

Определители (детерминанты) рассматриваются только для квадратных матриц.

Определитель n-го порядка это число, записываемое в виде таблицы

и может быть вычислено по элементам этой таблицы в соответствии с указанными ниже правилами.

Минором M_ij элемента a_ij называется определитель (n-1)-го порядка, полученный из определителя n -гопорядка вычеркиванием i -й строки и j -го столбца.

Алгебраическое дополнениеA_ij элемента a_ij определяется равенством:

A_ij=(-1)^i+jM_ij.

Определитель D_n (det) находится по правилу:

,

а миноры M_1k – являются определителем (n-1)-го порядка, полученным из D_n вычеркиванием 1-й строки и k -го столбца. Эта формула называется разложением по строке. Можно раскладывать по столбцу:

.

Определители первого, второго и третьего порядков

Определитель первого порядка .

Определитель второго порядка:

D₂= .

Определитель третьего порядка, вычисленный разложением по первой строке:

D₃= .

Правило вычисления определителя 3-го порядка равносильно правилу треугольников (правилу Саррюса):

D₃= a₁₁a₂₂a₃₃+ a₁₂a₂₃a₃₁+ a₂₁a₃₂a₁₃-(a₁₃a₂₂a₃₁+ a₁₂a₂₁a₃₃+ a₂₃a₃₂a₁₁).

Чтобы запомнить, какие произведения в правой части равенства берутся со знаком «+», а какие со знаком «–», полезно использовать следующее правило треугольников (или правило Саррюса):

Это правило позволяет легко записать формулу вычисления определителя 3-го порядка и найти его.