Методические указания и контрольные задания
Для студентов-заочников
По дисциплине: Математика
Заочное отделение
ТЕМА 1. КОМПЛЕКСНЫЕ ЧИСЛА. ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В РАЗНЫХ ФОРМАХ ЗАПИСИ
| Элементы содержания | Требования к знаниям и умениям |
| Действия над комплексными числами, заданными в алгебраической форме | знать: правила выполнения действий с комплексными числами в алгебраической форме уметь: выполнять действия над комплексными числами в алгебраической форме |
| Тригонометрическая форма комплексного числа | знать: формулы перехода от алгебраической формы к тригонометрической форме комплексного числа; правила выполнения действий над комплексными числами, заданными в тригонометрической форме уметь: находить тригонометрическую форму комплексного числа; выполнять действия над комплексными числами, заданными в тригонометрической форме |
| Решение уравнений | знать: определение комплексного числа уметь: находить корни квадратного уравнения с отрицательным дискриминантом |
| Сопряженные комплексные числа | знать: понятие сопряженных комплексных чисел уметь: записывать число, сопряженное заданному комплексному числу |
| Модуль комплексного числа | знать: понятие модуля комплексного числа уметь: вычислять модуль комплексного числа |
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
1. Определение комплексного числа.
Число 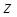 вида
вида 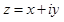 , где
, где 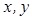 - любые действительные числа, а
- любые действительные числа, а 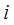 - так называемая мнимая единица, называется комплексным числом.
- так называемая мнимая единица, называется комплексным числом.
 или
или 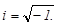
Действительные числа x и y называются соответственно действительной и мнимой частями комплексного числа z и обозначаются 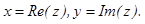
Рассмотрим частные случаи комплексных чисел.
· Пусть y =0, x - любое действительное число. Тогда 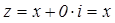 становится действительным числом.
становится действительным числом.
· Пусть 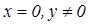 . Тогда
. Тогда  - чисто мнимое число.
- чисто мнимое число.
Таким образом, все действительные числа и все чисто мнимые числа входят в множество комплексных чисел.
Два комплексных числа  и
и 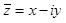 называются сопряженными комплексными числами.
называются сопряженными комплексными числами.
Сравнение комплексных чисел осуществляется по правилам:
1. Два комплексных числа  считаются равными, если
считаются равными, если 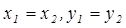 .
.
2. Комплексное число 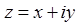 равно нулю только тогда, когда
равно нулю только тогда, когда  одновременно.
одновременно.
3. Операции <, > не имеют смысла на множестве комплексных чисел.
2. Геометрическое изображение комплексных чисел.
Рассмотрим декартову прямоугольную систему координат ХОУ на плоскости. Каждой точке плоскости при этом соответствуют вполне определенные координаты 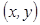 , а следовательно, и вполне определенное комплексное число
, а следовательно, и вполне определенное комплексное число  . Обратно, каждому к
. Обратно, каждому к 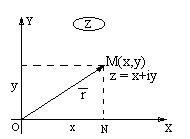 омплексному числу
омплексному числу 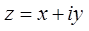 соответствует вполне определенная пара действительных чисел
соответствует вполне определенная пара действительных чисел 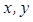 , а следовательно, и вполне определенная точка плоскости
, а следовательно, и вполне определенная точка плоскости 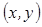 . Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа
. Таким образом установили связь между множеством точек на плоскости и множеством комплексных чисел. Плоскость, точки которой изображают комплексные числа 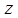 , называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа
, называется комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Очевидно, что изображением комплексного числа 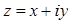 можно считать также и вектор
можно считать также и вектор  .
.
3. Тригонометрическая форма записи комплексного числа.
Длина вектора, изображающего комплексное число 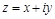 ,
, 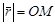 называется модулем комплексного числа.
называется модулем комплексного числа.
Угол j, образуемый этим вектором с положительным направлением действительной оси (Ð MON), называется аргументом комплексного числа.
Обозначение: модуль 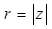 ,
,
аргумент  .
.
Из прямоугольного треугольника OMN

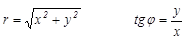 .
.
В качестве главного значения аргумента комплексного числа обычно выбирают значение 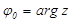 , определенное неравенствами
, определенное неравенствами
 ,
,
 .
.
Итак, 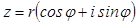 называется тригонометрической формой записи комплексногочисла.
называется тригонометрической формой записи комплексногочисла.
Пример.Записать в тригонометрической форме комплексные числа:
1. 
2. 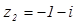
3. 
4. 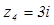 .
.
Решение:
1. 
 .
.
2.  .
.
 .
.
3. 
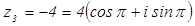 .
.
4. 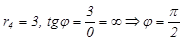
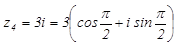 .
.
4. Действия над комплексными числами.
1. Сложение.
Суммой двух комплексных чисел 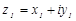 и
и  называется комплексное число
называется комплексное число  , определяемое равенством
, определяемое равенством
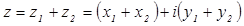 .
.
Из определения вытекают следующие законы сложения:
- Переместительный: 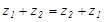
- Сочетательный: 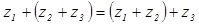
2. Вычитание.
Вычитание комплексных чисел определяется как действие, обратное сложению. Вычесть из числа  число
число  значит найти такое число
значит найти такое число 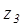 , чтобы имело место равенство:
, чтобы имело место равенство: 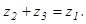 Число
Число  называется разностью чисел
называется разностью чисел  и
и 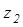 и обозначается
и обозначается 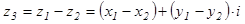 .
.
Вычитаниевсегдавыполнимо.
3. Умножение.
Произведением 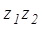 двух комплексных чисел
двух комплексных чисел 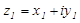 и
и  называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством 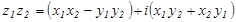 .
.
Из определения следуют законы:
· Переместительный 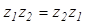
· Сочетательный 
· Распределительный 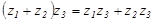 .
.
4. Деление.
Деление – действие, обратное умножению. Разделить комплексное число  на комплексное число
на комплексное число 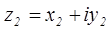 значит найти такое число
значит найти такое число 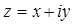 , чтобы имело место равенство
, чтобы имело место равенство 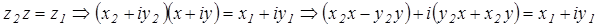 .
.
Тогда получаем систему для определения 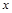 и
и  :
:

Система всегда разрешима, т.к. определитель
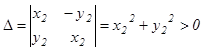 .
.
Число  называется частным.
называется частным.
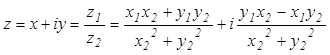 .
.
Итак, чтобы разделить одно комплексное число на другое, надо числитель и знаменатель дроби умножить на комплексное число, сопряженное числу, стоящему в знаменателе.
5. Умножение и деление комплексных чисел, заданных в тригонометрической форме.
Пусть  .
.
Тогда 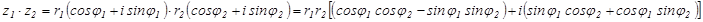
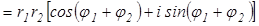 .
.
Следовательно, при умножении комплексных чисел их модули умножаются, а аргументы складываются: 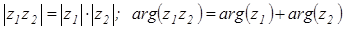 .
.
Деление комплексных чисел, записанных в тригонометрической форме, приводит к формуле:
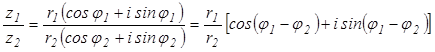 .
.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ:
Вариант 1
1. Решить квадратное уравнение:
х 2 + 2 х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
5 х – 2 у + (х + у) i = 4 + 5 i.
3. Выполнить действия:
a. 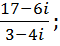
b. (1 - i)3;
c. i 40 – i 21.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 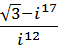
b. 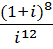
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 2
1. Решить квадратное уравнение:
х 2 + 2 х + 4 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
5 хi – 2+ 4у = 9 i + 2 x + 3 yi.
3. Выполнить действия:
a. 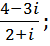
b. (1 + i)3;
c. i 3 – i 100.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 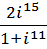
b. 
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 3
1. Решить квадратное уравнение:
х 2-6 х + 18 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
9 + 2 хi +4 уi = 10 i + 5 x – 6 y.
3. Выполнить действия:
a. 
b. (1 - i)4;
c. i 13 – i 33.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 
b. 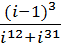
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 4
1. Решить квадратное уравнение:
х 2-4 х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
2 хi +3 уi + 17 = 3 x + 2 y + 18 i.
3. Выполнить действия:
a. 
b. (1 - i)4;
c. i 17 – i 38.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 
b. 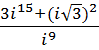
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 5
1. Решить квадратное уравнение:
х 2 + 6 х + 10 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
4 х +5 у – 9 + 7 (3 х - у) i = 10 x + 14 yi.
3. Выполнить действия:
a. 
b. (3 - 4 i)3;
c. i 15 – i 37.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 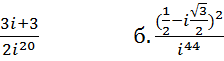
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 6
1. Решить квадратное уравнение:
х 2-10 х + 41 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
3 + 4 хi +5 уi =12 i + 5 x – 2 y.
3. Выполнить действия:
a. 
b. (2 + 5 i)3;
c. i 23 – i 111.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 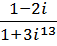
b. 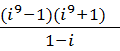
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 7
1. Решить квадратное уравнение:
2 х 2- 2 х + 5 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
х (2 + i) – у (1- i) = 1 + 3 i.
3. Выполнить действия:
a. 
b. (1 + 7 i)3;
c. i 45 – i 11.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 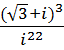
b. 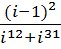
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 8
1. Решить квадратное уравнение:
25 х 2- 20 х + 13 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
х (1 + i) + y(2 – 3i) = 3i + 1.
3. Выполнить действия:
a. 
b. (1 - 5 i)3;
c. i 58 – i 51.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 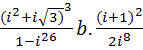
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 9
1. Решить квадратное уравнение:
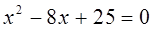 .
.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
9 + 2 ix+4iy = 10 i+5x-6y.
3. Выполнить действия:
a. 
b. (3 - 2 i)3;
c. i 15 – i 57.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости
Вариант 10
1. Решить квадратное уравнение:
х 2-6 х + 18 = 0.
2. Найти действительные числа x и y из условия равенства двух комплексных чисел
2 хi +3 уi+ 17 = 3 x + 2 y + 18.
3. Выполнить действия:
a. 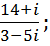
b. (1 - 2 i)4;
c. i 23 – i 35.
4. Выполнить действия и записать результат в тригонометрической форме:
a. 
5. Изобразить решения, полученные в пункте 4, на комплексной плоскости.
ПРИМЕРЫ РЕШЕНИЙ
1. Решите во множестве комплексных чисел уравнение 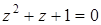 .
.
Решение:
Так как 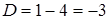 , тогда корни находятся по формуле
, тогда корни находятся по формуле 
( ).
).
Отсюда,  ,
,  .
.
Ответ:  .
.
.
Решите уравнение 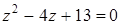
Решение:
По формуле 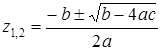 , находим:
, находим:
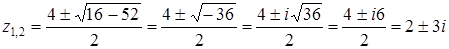 .
.
2. При каких действительных значениях x и y комплексные числа 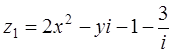 и
и  будут равными?
будут равными?
Решение:
Комплексные числа 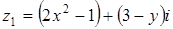 и
и 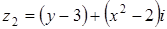 будут равными, если выполняются условия:
будут равными, если выполняются условия:
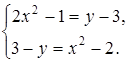

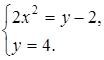
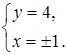
Ответ: 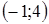 ;
; 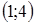 .
.
3. Вычислите 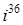 ;
;  ;
; 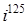 ;
; 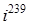 .
.
Решение:
С помощью формулы: 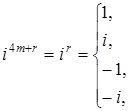

легко получаем:
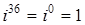 ;
;
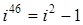 ;
;
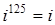 ;
;
 .
.
Ответ:  ;
; 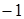 ;
;  ;
;  .
.
4. Выполнить все действия над комплексными числами  и
и  .
.
Решение
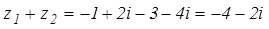
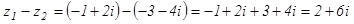

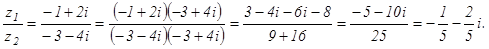
5. Выполните указанные действия:  .
.
Решение
Вычислим значение дроби 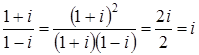 .
.
Следовательно, 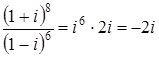
Ответ:  .
.
6. Изобразите на комплексной плоскости следующие комплексные числа:
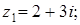

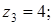
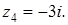
Решение
Данным комплексным числам соответствуют точки комплексной плоскости.
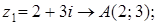
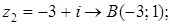


Покажем их.

7. Запишите комплексные числа в тригонометрической форме:
а)  ; б)
; б)  ; в)
; в) 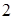 ; г)
; г)  ; д)
; д) 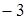 ; е)
; е) 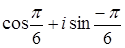 ; ж)
; ж) 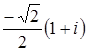 .
.
Решение
Так как тригонометрическая форма комплексного числа имеет вид  , тогда:
, тогда:
а) В комплексном числе 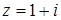 :
: 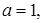
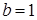 .
.
Тогда 
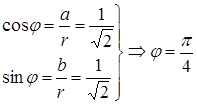 ,
,
Поэтому 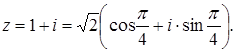
б) 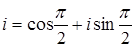 , где
, где 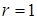 ,
, 
в) 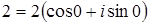 , где
, где 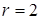 ,
, 
г) 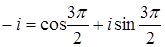 , где
, где 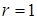 ,
, 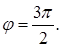
д)  , где
, где  ,
, 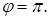
е) 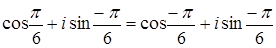 .
.
ж)  , а
, а 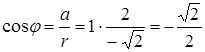 , то
, то  .
.
Поэтому 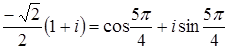
Ответ:  ;
;  4;
4;  ;
; 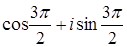 ;
;  ;
;  ;
;  .
.






