ФИЗИКИ АТОМА
Корпускулярно-волновой дуализм.
Формула де Бройля
В явлениях интерференции, дифракции, поляризации, дисперсии и других, свет проявляет волновые свойства, т.е. это электромагнитная волна с l = с/n и w = 2pn.
В явлениях теплового излучения, фотоэффекте, эффекте Комптона свет представляет поток фотонов с E = hn и p = E /c = h/l.
Таким образом, свет может проявлять как волновые, так и корпускулярные свойства, т.е. имеет двойственную природу (корпускулярно - волновой дуализм). В 1924 г. Французский физик Луи де Бройль предположил, что двойственная природа свойственна любым движущимся частицам, а не только фотонам. Частице с энергией Е и импульсом p соответствует волна с длиной волны и частотой, определяемых выражениями
l = h/p; n = E/h. (7.1)
Эти формулы называются соотношениями де Бройля. Волны де Бройля имеют вероятностное, статистическое толкование и не имеют аналогов в классической физике. В 1927 г. гипотеза получила экспериментальное подтверждение – К. Дэвидсон и Л. Джермер наблюдали дифракцию электро- нов на пластинах Ni. В дальнейшем волновые свойства были обнаружены у протонов, нейтронов и других микрочастиц. Опытами Фабриканта и других было показано, что волновые свойства характерны не только для ансамбля частиц, но и для отдельной частицы.
Таким образом, корпускулярно-волновой дуализм микрочастиц - объективная реальность.
Соотношение неопределенностей
Состояние классической частицы полностью определяется ее координатами и импульсом. Зная начальное положение частицы и действующие силы, можно записать и решить уравнение движения (2-ой закон Ньютона) и тем самым определить координаты и импульс частицы для любого момента времени.
Для микрочастицы, вследствие наличия у нее волновых свойств, ситуация другая.
Пусть частица движется вдоль оси Х. Если точно определена координата частицы, то ничего нельзя сказать о ее импульсе, т.к. в соответствии с формулой де Бройля он определяет длину соответствующей волны, но понятие длины волны в данной точке не имеет смысла. Если же точно задан импульс частицы, то получаем монохроматическую волну, имеющую бесконечную протяженность, т.е. не определена координата частицы. Таким образом, координата и импульс частицы не могут быть одновременно определены точно, всегда будет погрешность. Можно показать, что это справедливо не только для координат и соответствующего импульса, но и для энергии и времени. Степень точности задается соотношениями неопределенности (соотношениями Гейзенберга):
Dx . Dpx ³ h,
Dy . Dpy ³ h, (7.2)
Dz . Dpz ³ h,
Dt . DE ³ h.
В силу малой величины h эти соотношения существенны только в микромире и не проявляются в опытах с макроскопическими телами.
Из этих соотношений следует несколько выводов:
1) микрочастица не может находиться в покое;
2) нельзя разделять полную энергию микрочастицы на кинетическую и потенциальную;
3) принципиально невозможно точно определить одновременно координату и импульс частицы.
Уравнение Шредингера
Наличие волновых свойств у микрочастиц не позволяет описывать их с помощью классического уравнения динамики, дающего возможность по заданным силам и начальным условиям найти для любого момента времени координаты частицы и её скорость (импульс). Возникла необходимость получения основного уравнения квантовой механики, которое позволило бы решить аналогичные задачи, но с учётом волновых свойств частиц. Такое уравнение было получено в 1929г. Шредингером. Оно как и уравнения Ньютона, не выводится, а постулируется как основной закон природы. Единственным доказательством его справедливости может быть лишь экспериментальная проверка выводимых из него следствий. Такую проверку уравнение Шредингера выдержало.
В нерелятивистской квантовой механике уравнение имеет вид:
, (7.3)
где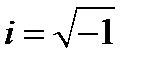 
, m – масса частицы, U(x,y,z,t) – потенциальная энергия частицы в силовом поле, в котором она движется, 
- дифференциальный оператор Лапласа, Y(x,y,z,t) – волновая функция частицы.
Это уравнение является волновым уравнением, решение которого позволяет найти волновую функцию (пси-функцию), однозначно описывающую состояние микро- частицы в любых условиях. Физический смысл имеет не сама волновая функция, а квадрат ее модуля, определяющий плотность вероятности пребывания частицы в данной точке пространства
(7.4)
где Y* - величина, комплексно сопряженная с Y, а dp/dV – плотность вероятности (вероятность, отнесенная к единице объема) пребывания частицы в данной точке пространства. Вероятность нахождения частицы в объеме V определяется формулой
. (7.5)
Связь волновой функции и вероятности приводит к следующим ограничениям на волновую функцию: она должна быть непрерывной, конечной, однозначной, иметь непрерыв- ные производные, удовлетворять условию нормировки
, (7.6)
(наличие частицы в какой либо точке бесконечного пространства - достоверное событие, его вероятность равна 1).
Если потенциальная энергия U(x,y,z) не зависит от времени, то в уравнении волны волновую функцию можно разделить на временную и пространственную части и представить его в виде
, (7.7)
где E – полная энергия частицы, w = E/ ħ. Подставляя эту формулу в общее уравнение, для пространственной части волновой функции получаем:
. (7.8)
Это уравнение называется стационарным уравнением Шредингера или уравнением для стационарных состояний, т.к. плотность вероятности не зависит от времени. Функции Y, удовлетворяющие уравнению, называются собственными функциями, а значения Е, при которых существуют решения – собственными значениями энергии.
Рассмотрим несколько примеров решения этого уравнения.
