Рассмотрим движение микрочастицы в одномерной прямоугольной потенциальной яме длиной l с бесконечно высокими стенками (рис.7.1). Тогда для потенциальной энергии имеем: U = 0 при 0 £ x £ l и U = ∞ при x < 0 и x > l. Внутри ямы уравнение Шредингера имеет вид
,
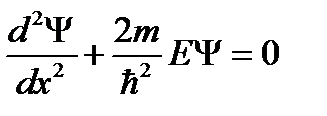или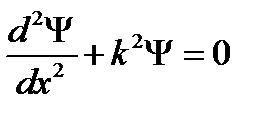 
, (7.12)
| Е4 Е3 Е2 Е1 l x |
| U 0 |
| Рис.7.1 |
Решение уравнения записы- вается в виде
Ψ(x)=Asin(kx)+Bcos(kx), (7.13)
где A и B – постоянные, которые определяются из граничных условий.
Вероятность нахождения частицы вне ямы равна нулю, следовательно, волновая функция вне ямы и на ее границах (в силу непрерывности) также равна 0:
Ψ(0)=Ψ(l)= 0.
Из первого условия Ψ(0)= B получаем B = 0, из второго
Ψ(l)= A sin(k l)= 0
следует, что k l = np или k = np / l, где n = 1, 2, 3 … (n = 0 соответствует Ψ = 0, т.е. отсутствию частицы в яме).
Тогда для собственных значений энергии получаем выражение
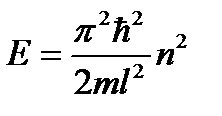, (n = 1, 2, 3 …). (7.14)
Таким образом, энергия и импульс частицы в потенциальной яме могут принимать лишь определенные, дискретные значения, т.е. квантуются (рис.7.1). Минимальное значение энергии равно E = p 2ħ2/(2ml2), т.е. частица в яме не может покоиться, что находится в соответствии с соотношениями неопределенности.
Интервал энергии между соседними уровнями составляет
.
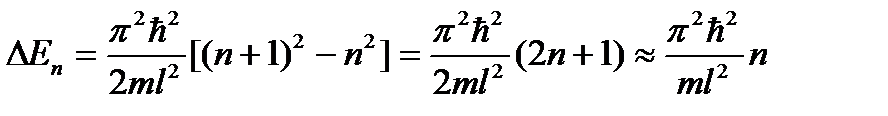Рассмотрим несколько примеров. Для молекул идеального газа (m = 10-26 кг, l = 0,1 м) DEn = 10-20× n эВ, для свободных электронов в металле (m»10-30 кг, l =0,1 м) DEn =10 -16× n эВ, т.е. в этих случаях можно считать, что энергия меняется непрерывно. Для электрона в атоме (m»10-30 кг, l =10-10 м) DEn =102× n эВ. Следовательно, здесь квантование существенно и можно говорить лишь о дискретном спектре энергии.
Относительное расстояние между уровнями DEn/En» 2/n уменьшается с увеличением квантового числа n, уровни располагаются ближе и спектр энергии становится квазинепрерывным.
В этом выражается принцип соответствия Бора: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.
Для определения постоянной A в волновой функции используем условие нормировки:
,
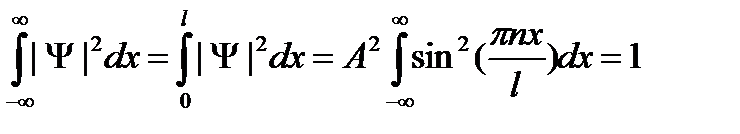откуда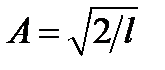 
.
Таким образом, собственные функции выражаются формулой
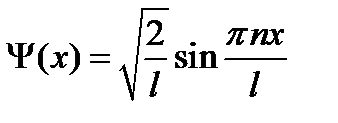, n = 1, 2, 3… (7.15)
Графики собственных функций и соответствующие плотности вероятности приведены на рис.7.2.
Из рисунка видно, что в разных квантовых состояниях есть точки, в которых плотность вероятности обнаружения частицы равна нулю. Такое поведение частицы несовместимо с классическими представлениями о траектории движения и равновероятности всех положений частицы.
| a) в) Рис.7.2 |
| n =3 n =2 n =1 |
| 0 l x |
| n =3 n =2 n =1 |
| 0 l x |
| Y(x) |
| ïY(x)ï2 |
Из формулы 7.15 и рис. 7.2 следует, что существуют лишь такие состояния частицы в потенциальной яме, при которых на ширине ямы укладывается целое число полуволн де Бройля. Здесь можно провести аналогию с механическими волнами. Для колеблющейся струны или закрытого акустического резонатора возникающие стоячие волны удовлетворяют такому же условию, все остальные волны существовать не могут, они затухают.
