Пусть
х1,…,хn (4.1)
выборка (независимая) из некоторого распределения с плотностью р(х; 
)=р(х1,…,хn; ), зависящей от параметра , который может изменяться в интервале 0 < < 1. Пусть у(х1,…,хn) - некоторая статистика (т.е. функция от выборки) и F(х; )=Р{η≤ х} – функция распределения случайной величины η= у(х1,…,хn), когда выборка (4.1) имеет распределение с плотностью р(х1,…,хn; ). Предположим, что F(х; ) есть убывающая функция от параметра . Обозначим 
квантиль распределения F(х; ), т.е. корень уравнения F (х; ) =1-γ.
В этом случае квантиль есть возрастающая функция от . Зададимся малым числом α>0, например, α= 0,05 или α =0,01. Пусть α=α1+α 2. При каждом неравенства
(4.2)
выполняются с вероятностью 1-α, близкой к единице. Обозначим функцию, обратную , т.е. решение уравнения
у=
через = 
.
Тогда неравенства (4.2) при любом выполняются с вероятностью 1-α. Обозначим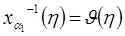 
, 
и запишем (4.3) в следующем виде:
(
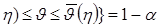. (4.4)
Интервал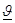 
(
называется доверительным интервалом для параметра , а вероятность 1-α доверительной вероятностью.
Следует различать смысл неравенств (4.2) и (4.3). В неравенстве (4.2) при любом случайная величина ξ попадает в указанный интервал с вероятностью 1-α.
В неравенстве (4.3) параметр неслучайный, а концы интервала случайны, поэтому правильнее будет говорить, что при любом доверительный интервал (со случайными концами) покрывает параметр с доверительной вероятностью 1-α.
Доверительный интервал (4.4), кроме доверительной вероятности 1-α, имеет еще одну характеристику - среднюю длину:
(
.
Мы должны стараться среди всех доверительных интервалов с доверительной вероятностью 1-αвыбрать тот, который имеет наименьшую длину.
Если статистика η=у(х1,…,хn) уже выбрана, то мы можем варьировать разложение αна сумму α 1+ α 2.
В дальнейшем мы встретимся со следующими двумя случаями.
Случай 1. Функция распределения F (х; ) имеет вид F (х - ). В этом случае F (х - ) убывает с ростом . Легко видеть, что при этом
= + 
и 
,
поэтому доверительный интервал (4.3) имеет вид:
(4.5)
Случай 2. Параметр положителен, и F(х; )= 
, F(0)=0. В этом случае при х >0 убывает с ростом , и
= · 
и 
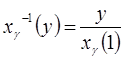
Доверительный интервал (4.3) в этом случае имеет вид:
Доверительные интервалы для параметров
Нормального распределения
Пусть независимая выборка (4.1) взята из нормального распределения с параметрами (а, σ).
а) Доверительный интервал для а при известном σ.
Возьмем за статистику η среднее 
. Это разумно, так как есть достаточная статистика относительно а и является эффективной оценкой а.
Как известно, имеет нормальное распределение с параметрами (а, 
). Обозначим, как и раньше, uγ - квантиль нормального распределения, т.е. 1 -Ф0(uγ)=γ (Ф0(u) - функция распределения нормального распределения).
Пусть α = α 1+ α 2 . Так как u1-γ=- uγ, то неравенство
(4.6)
выполняется с вероятностью 1-α. Разрешая неравенство (4.6) относительно а, имеем доверительный интервал для а
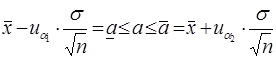, (4.7)
являющийся частным случаем для (4.5).
Доверительная вероятность (4.7) равна 1-α, а его длина
.
Эта длина будет наименьшей, если взять α1=α 2=α2/2.
б) Доверительный интервал для а при неизвестном σ.
Пусть
, 
.
Теорема 1. Статистики 
для выборки (4.1) из нормального распределения независимы. Случайная величина
·(n -1)/σ2 имеет c2 - распределение с (n -1) - й степенью свободы.
Доказательство.
Случайные величины 
независимы и имеют нормальное распределение с параметрами (0, 1). Обозначим
, 
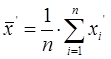тогда
, 
.
Докажем, что 
и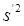 
независимы и что 
·(n-1) имеет c2 - распределение с (n-1)- й степенью свободы. Случайный вектор (х1´,…,хn´) имеет сферическое нормальное распределение с плотностью
(4.8)
Переход от одного ортогонального базиса в Rn к другому осуществляется при помощи преобразования координат
,
коэффициенты которого связаны между собой соотношениями 
. Такое преобразование называется ортогональным.
Пусть у=С·х´ - ортогональное преобразование, заданное соотношениями:
,
, 
.
Тогда у1,у2,…,уn также будут иметь сферически нормальные распределения с плотностью (4.8). Так как у 1=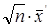 
и 
= 
(из-за ортогональности преобразования С), то
(n-1) · = 
= 
,
поэтому (n-1) · не зависит от 
имеет распределение c2 с (n-1)- й степенью свободы. Теорема доказана.
Следствием только что доказанной теоремы является
Теорема 2. Пусть (4.1) - независимая выборка из нормального распределения. Статистика:
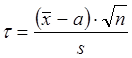, (4.10)
называемая отношением Стьюдента, имеет распределение Стьюдента с (n-1)- й степенью свободы.
Доказательство. Случайная величина 
имеет нормальное распределение с параметрами (0,1), а S/σ не зависит от 
и равно 
, где 
имеет c2 - распределение с (n-1) -й степенью свободы. Поэтому отношение (4.10) имеет распределение Стьюдента с (n-1)- й степенью свободы. Теорема доказана.
Для построения доверительного интервала для а при неизвестном σ воспользуемся отношением Стьюдента (4.10). Пусть Sn(t)- функция распределения Стьюдента с n степенями свободы:
, 
.
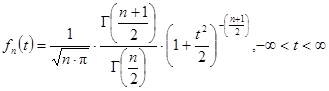Обозначим tγ(n) - квантиль распределения Sn(t), т.е. корень уравнения
Sn(t)=1-γ.
Так как распределение Стьюдента симметрично, 
t1-γ(n)= -tγ(n) и при построении доверительного интервала надо брать α1=α2=α/2. Неравенство
выполняется с вероятностью 1-α. Это дает нам доверительный интервал
в) Доверительный интервал для σ при известном a.
Статистика
является достаточной для оценки параметра σ и имеет c2 - распределение с n степенями свободы. Обозначим через Кn(х) функцию распределения 
и через кγ(n) – квантиль Кn(х),
.
Квантиль кγ(n) – корень уравнения
Кn(х)= 1-γ.
Пусть α=α1+α2 . Тогда неравенства
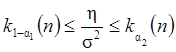
выполняется с вероятностью 1-α.
Это дает нам доверительный интервал
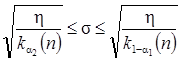(4.11)
г) Доверительный интервал для σпри неизвестном a.
В этом случае за основную статистику η возьмем эмпирическую дисперсию.
По теореме 1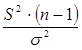 
имеет c2 - распределение с (n -1) - й степенью свободы. Это приводит к доверительному интервалу, аналогичному (4.11)
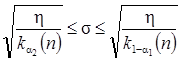
с доверительной вероятностью 1-(α1+α2).
Обычно на практике используют значения 1-α равные 0.9, 0.95 или 0.99.
