На примере выборок из нормального распределения разберем те задачи, которые возникают при проверке сложных гипотез.
Пример 3. Пусть независимая выборка (1.1) взята из нормального распределения с параметрами  , причем
, причем  известно. Рассмотрим простую проверяемую гипотезу
известно. Рассмотрим простую проверяемую гипотезу  и одностороннюю сложную гипотезу
и одностороннюю сложную гипотезу  . Действуя также, как в п.2.4 при различении двух простых гипотез, находим, что критерий
. Действуя также, как в п.2.4 при различении двух простых гипотез, находим, что критерий
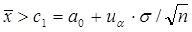 будет иметь уровень значимости
будет иметь уровень значимости  и будет наиболее мощным для любой простой гипотезы
и будет наиболее мощным для любой простой гипотезы  Функция мощности этого критерия
Функция мощности этого критерия 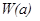 будет иметь график, изображенный на рис.3, и ошибка II рода:
будет иметь график, изображенный на рис.3, и ошибка II рода: 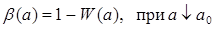
 |
Рис.3
в пределе равна  . Поэтому по критерию
. Поэтому по критерию  мы можем лишь с малой ошибкой
мы можем лишь с малой ошибкой  отвергнуть гипотезу
отвергнуть гипотезу  . В случае
. В случае  , мы не имеем больших оснований утверждать только на основе выборки (1.1), что
, мы не имеем больших оснований утверждать только на основе выборки (1.1), что  а не
а не  так как при
так как при 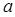 близких к
близких к  вероятность события
вероятность события  близка к единице. Поэтому при
близка к единице. Поэтому при  мы говорим, что выборка (1.1) не противоречит гипотезе
мы говорим, что выборка (1.1) не противоречит гипотезе  , и если эта гипотеза имеет какое-либо обоснование, независимое от выборки (1.1), то выборка в этом случае ее подтверждает.
, и если эта гипотеза имеет какое-либо обоснование, независимое от выборки (1.1), то выборка в этом случае ее подтверждает.
Пример 4. Пусть гипотеза  остается прежней, а конкурирующая гипотеза будет двусторонней
остается прежней, а конкурирующая гипотеза будет двусторонней  . В этом случае для значений
. В этом случае для значений  и
и  терема Неймана-Пирсона дает разные оптимальные критерии
терема Неймана-Пирсона дает разные оптимальные критерии  , т.е. не существует такого критерия с уровнем значимости
, т.е. не существует такого критерия с уровнем значимости  , который максимизировал бы функцию мощности
, который максимизировал бы функцию мощности 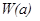 во всех точках
во всех точках  . В этом случае применяют двусторонний критерий, по которому гипотеза
. В этом случае применяют двусторонний критерий, по которому гипотеза  отвергается, когда
отвергается, когда
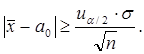
Функция мощности такого критерия равна:
 .
.
 Уровень значимости критерия равен
Уровень значимости критерия равен  , график изображен на рис.4.
, график изображен на рис.4.
Рис. 4.
Пример 5. Сравнение двух дисперсий.
При обработке наблюдений часто возникает необходимость сравнить две или несколько дисперсий. Основная гипотеза, которая при этом проверяется: можно ли сравниваемые выборочные дисперсии оценками одной и той же генеральной дисперсию рассмотрим две независимые выборки из нормальных распределений:

 ,
,
средние значения которых соответственно равны  .
.
Выборочные дисперсии:
 ,
, 
определяются со степенями свободы:
 ,
, 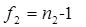 .
.
Требуется выяснить, являются ли выборочные дисперсии  значимо различными или же полученные выборки можно рассматривать как взятые из генеральных совокупностей с равными дисперсиями.
значимо различными или же полученные выборки можно рассматривать как взятые из генеральных совокупностей с равными дисперсиями.
Предположим, что первая выборка сделана из генеральной совокупности с дисперсией  , а вторая- из генеральной совокупности с дисперсией
, а вторая- из генеральной совокупности с дисперсией  . Проверяется нулевая гипотеза о равенстве генеральных дисперсий
. Проверяется нулевая гипотеза о равенстве генеральных дисперсий  :
: 
 .
.
Чтобы отвергнуть эту гипотезу, нужно доказать значимость различий между  при выбранном уровне значимости
при выбранном уровне значимости  . В качестве критерия значимости обычно используется критерий Фишера.
. В качестве критерия значимости обычно используется критерий Фишера.
Распределением Фишера ( -распределением,
-распределением,  -распределением) называется распределение случайной величины (статистики):
-распределением) называется распределение случайной величины (статистики):
 (2.16)
(2.16)
Плотность вероятности  -распределения:
-распределения:
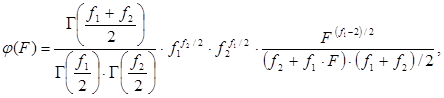
Пусть  -квантиль
-квантиль  -статистики (2.16), тогда
-статистики (2.16), тогда 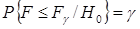 .
.
Квантили  -распределения обладают свойством:
-распределения обладают свойством:

В условиях нулевой гипотезы 
 и
и  , и, следовательно,
, и, следовательно,  -распределение может быть непосредственно использовано для оценки отношения выборочных дисперсий
-распределение может быть непосредственно использовано для оценки отношения выборочных дисперсий  . При доверительной вероятности
. При доверительной вероятности  двусторонняя оценка величины
двусторонняя оценка величины  имеет вид:
имеет вид:  или
или

В условиях нулевой гипотезы 
 , следовательно, с вероятностью
, следовательно, с вероятностью 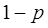 : должно выполняться двустороннее неравенство:
: должно выполняться двустороннее неравенство:
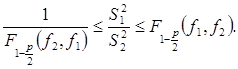 (*)
(*)
Вероятность неравенств, противоположных данным, равна уровню значимости 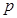 , они образуют критическую область для нулевой гипотезы. Если полученное дисперсионное отношение попадает в критическую область, различие между дисперсиями надо считать значимыми (нуль гипотеза
, они образуют критическую область для нулевой гипотезы. Если полученное дисперсионное отношение попадает в критическую область, различие между дисперсиями надо считать значимыми (нуль гипотеза  отвергается).
отвергается).
При проверке нулевой гипотезы 
 односторонний критерий применяется, если альтернативной гипотезой является гипотеза
односторонний критерий применяется, если альтернативной гипотезой является гипотеза 
 (для определенности
(для определенности  - большая дисперсия, т.е.
- большая дисперсия, т.е.  ), т.е. большей выборочной дисперсии
), т.е. большей выборочной дисперсии  заведомо не может соответствовать меньшая генеральная.
заведомо не может соответствовать меньшая генеральная.
При этом различие между дисперсиями следует считать значимым, если:
 (**)
(**)
Двусторонний критерий значимости применяется для альтернативной гипотезы 
 , т.е. когда соотношение между генеральными дисперсиями неизвестно. При этом в неравенстве (*) надо проверять только правую часть, т.к. левая часть всегда выполняется: по условию
, т.е. когда соотношение между генеральными дисперсиями неизвестно. При этом в неравенстве (*) надо проверять только правую часть, т.к. левая часть всегда выполняется: по условию  , а
, а 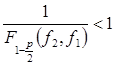 для небольших
для небольших  . При этом различие между дисперсиями следует считать значимым, если
. При этом различие между дисперсиями следует считать значимым, если 
 .
.
Критерий Фишера можно использовать для сравнения дисперсий, если одна из дисперсий является генеральной. Число степеней свободы генеральной дисперсии считается равным  .
.
Пример. 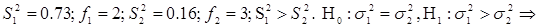 применяем односторонний критерий значимости (**). Дисперсионное отношение
применяем односторонний критерий значимости (**). Дисперсионное отношение  надо сравнить с табличным для уровня значимости
надо сравнить с табличным для уровня значимости  и чисел степеней свободы
и чисел степеней свободы 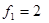 и
и 
 .
.
Таким образом, выборочное дисперсионное отношение меньше табличного и данные не позволяют считать дисперсии значимо различными.






