Мы будем иметь дело с независимой выборкой
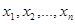 . (3.1)
. (3.1)
Из распределения 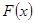 принадлежащего некоторому семейству распределений
принадлежащего некоторому семейству распределений 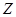 . Пусть
. Пусть 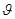 – параметр, однозначно определяемый по каждому распределению
– параметр, однозначно определяемый по каждому распределению 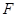 из семейства
из семейства 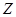 . Например,
. Например,
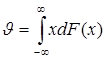 или
или 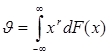 .
.
Таким образом, 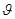 =
= 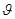 (F) - это значение функционала от распределения
(F) - это значение функционала от распределения 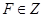 . Очень часто мы будем предполагать, что само семейство
. Очень часто мы будем предполагать, что само семейство 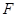 определяется одним или несколькими такими параметрами.
определяется одним или несколькими такими параметрами.
Тогда любая 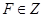 есть функция распределения
есть функция распределения 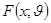 или
или 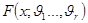 зависящая от одного или нескольких параметров. Такое семейство распределений называется параметрическим. В любом из этих случаев задача оценки (оценивания) параметра
зависящая от одного или нескольких параметров. Такое семейство распределений называется параметрическим. В любом из этих случаев задача оценки (оценивания) параметра 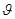 состоит в нахождении такой функции
состоит в нахождении такой функции
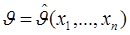 (3.2)
(3.2)
от выборки (3.1), которая в каком-то смысле близка к параметру 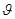 , если выборка взята из распределения
, если выборка взята из распределения 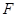 с
с 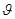 (
(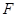 )=
)= 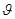 .
.
При этом предполагается, что функция (3.2) не зависит от значения оцениваемого параметра 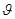 и других неизвестных параметров, от которых может зависеть
и других неизвестных параметров, от которых может зависеть 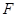 .
.
Вообще, любая функция вида (3.2) от выборки носит название статистики. Таким образом, 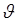 - это статистика (3.2).
- это статистика (3.2).
Оценка 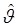 =
= 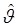 (
(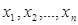 ) называется несмещенной, если при любом возможном
) называется несмещенной, если при любом возможном 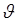
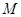
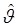 =
= 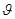 , (3.3)
, (3.3)
т.е. среднее значение 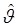 равно
равно 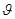 .
.
Приведем примеры несмещенных оценок. Если выборка (3.1) взята из семейства с конечным r -м моментом
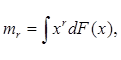
то выборочный r -й момент
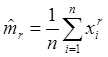 (3.4)
(3.4)
будет несмещенной оценкой mr, так как
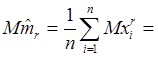
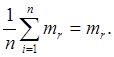
В частности, выборочное среднее 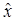 есть несмещенная оценка математического ожидания
есть несмещенная оценка математического ожидания  .
.
Выборочная дисперсия 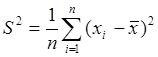 не является несмещенной оценкой дисперсии
не является несмещенной оценкой дисперсии 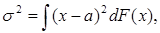 так как
так как 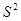 может представить в виде
может представить в виде
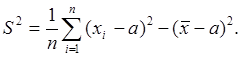
Отсюда
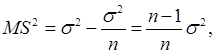 (3.5)
(3.5)
поскольку 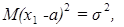 то
то 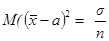 .
.
Равенство (3.5) дает нам возможность построить несмещенную оценку дисперсии
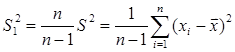 . (3.6)
. (3.6)
Заметим, что из несмещенности оценки S12 для σ2 не следует несмещенность оценки S1 для σ. Поэтому при большом числе N выборок (3.1) для оценки σ предпочтительнее пользоваться оценкой 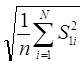 , а не
, а не 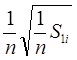 , где S1i - значение выборочной несмещенной дисперсии (3.6) для i -й выборки. Заметим, что обычно вместо S12 в (3.6) пользуются обозначением S2.
, где S1i - значение выборочной несмещенной дисперсии (3.6) для i -й выборки. Заметим, что обычно вместо S12 в (3.6) пользуются обозначением S2.
Очень часто нас интересуют асимптотические свойства оценок 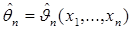 для выборок (1.1) объема
для выборок (1.1) объема 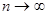 . Оценка
. Оценка 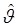 n (вернее, последовательность оценок
n (вернее, последовательность оценок 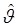 n) называется состоятельной, если при n →∞ она сходится по вероятности к параметру.
n) называется состоятельной, если при n →∞ она сходится по вероятности к параметру.
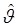 n
n 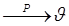
{ 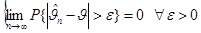 }
}
Примером состоятельной оценки может служить выборочный r -й момент 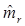 в (3.4), так как при конечности mr по усиленному закону больших чисел (если ξ1,ξ2, …- независимые, имеющие
в (3.4), так как при конечности mr по усиленному закону больших чисел (если ξ1,ξ2, …- независимые, имеющие 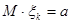 , то
, то 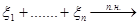 =
= 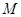 ξ, п.н. – почти наверное, т.е. с вероятностью = 1).
ξ, п.н. – почти наверное, т.е. с вероятностью = 1).
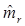
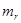 при
при 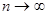 , следовательно,
, следовательно, 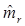
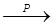
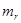 .
.
Для установления состоятельности оценки 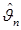 полезна следующая
полезна следующая
Теорема 1. Если при 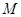
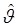 n
n 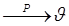
и 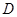
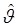 n→
n→  при
при 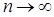 , то оценка
, то оценка 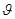 n - состоятельная.
n - состоятельная.
Доказательство.
По неравенству Чебышева при любом 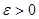
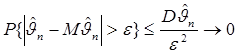 . (3.7)
. (3.7)
Из (3.7) и неравенства
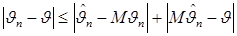
cледует, что при n →∞ вероятность события 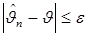 стремится к нулю, что и требовалось доказать.
стремится к нулю, что и требовалось доказать.






