В математической статистике часто требуется проверить гипотезу, что независимая выборка
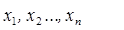(2.17)
взята из генеральной совокупности с функцией распределения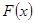 
. Относительно конкурирующей гипотезы, кроме независимости 
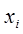в (2.17), других предположений не делается. В этом случае применяются так называемые непараметрические статистические критерии, которые строятся на основе какой-либо статистики 
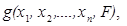зависящей от 
, причем распределение этой статистики при справедливости основной гипотезы известно точно и асимптотически при 
. Обычно статистика положительна, и при любой конкурирующей гипотезе ее значение вырастает.
Выбирается такое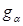 
, чтобы 
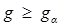при основной гипотезе выполнялось с вероятностью ошибки I рода 
.
Основная гипотеза принимается, если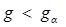 
и отвергается, если .
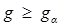Одним из наиболее известных таких критериев является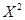 
-критерий Пирсона.
Выберем точки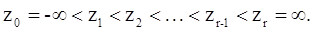 
Обозначим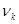 
число тех 
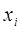из выборки (2.17), которые удовлетворяют условию 
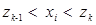. Тогда при справедливости основной гипотезы случайные величины
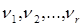(2.18) имеют полиноминальное распределение:
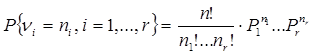, (2.19)
.
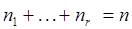Первоначальную задачу мы редуцируем теперь к проверке гипотезы о том, что частоты (2.18) получены из номинального распределения (2.19) с вероятностями
.
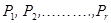Статистика, на основе которой строится критерий, называется 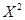-статистикой Пирсона и определяется суммой:
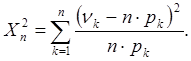(2.20)
Теорема 2. Распределение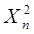 
при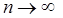 
слабо сходится к 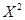-распределению с 
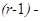й степенью свободы с функцией распределения.
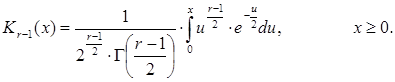(2.21)
Данный факт применяется следующим образом. Задаемся уровнем значимости . Тогда в силу теоремы 2, при больших 
с вероятностью, приближенно равной выполняется неравенство:
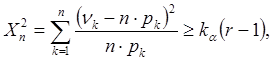(2.22) где 
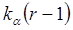- -квантиль 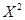-распределения с 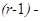й степенью свободы, т.е.
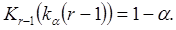(2.23)
Мы считаем основную гипотезу принятой, если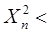 
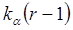, и отвергнутой, если выполнено обратное неравенство.
Выбор точек деления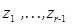 
должен удовлетворять двум требованиям. Во-первых, вероятности 
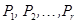должны достаточно хорошо отражать вид функции распределения 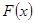(для этого 
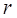должно быть больше, а 
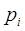меньше). Во-вторых, для того, чтобы можно было пользоваться предельной теоремой 
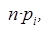и соответственно, 
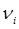должны быть не очень маленькими (для этого r не должно быть очень большим). Обычно на практике требуют, чтобы
, 
.
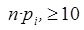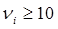Из этих противоположных требований и выбираются точки .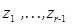
Другим примером непараметрического критерия является критерий Колмогорова. Этот критерий основан на статистике:
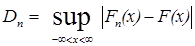, (2.24)
где 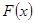-непрерывная функция распределения генеральной совокупности, 
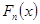-эмпирическая (выборочная) функция распределения, построенная по выборке (1.1):
, 
(
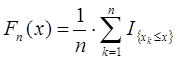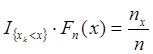, где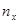 
- число выборочных значений, расположенных левее 
).
Докажем, что распределение случайной величины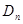 
инвариантно относительно .
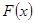Теорема 3. Если 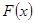непрерывна, то распределение статистики 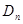не зависит от .
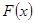Доказательство.
Докажем, что 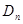при любой непрерывной 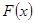имеет такое же распределение, как и в случае, когда 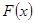задает равномерное распределение на отрезке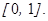 
Пусть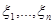 
- независимые случайные величины и каждая их них имеет функцию распределения .
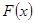Предположим, что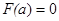 
, 
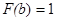и 
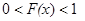при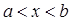 
, причем 
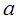и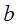 
могут быть бесконечными. Обозначим через 
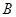множество, состоящее из тех точек 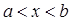, для которых при любом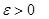 
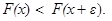Нетрудно видеть, что при любом 
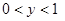существует единственная точка 
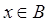, для которой 
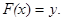Примем это 
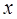за значение обратной функции
.
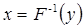Введем случайные величины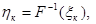 
, 
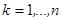. Они независимы, так как 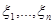- независимы и равномерно распределены в 
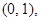так как события 
и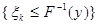 
равносильны и при любом 
.
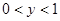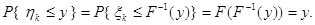
Обозначим более подробно эмпирические функции распределения для выборок 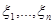и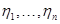 
:
.
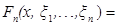
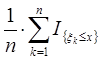
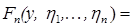
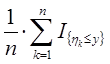Положим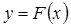 
, 
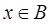. Тогда из равносильности событи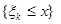й
и следует
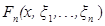. (2.25)
Верхнюю грань в (2.24) можно брать по 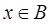, поэтому в силу (2.25) с вероятностью 1:
,
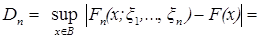
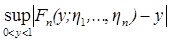что и требовалось доказать.
А.Н.Колмогоров доказал, что при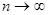 
для любой непрерывной 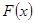имеет место следующее соотношение: 
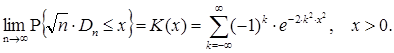(2.26)
На основе предельного соотношения (2.26) строится непараметрический критерий Колмогорова. Пусть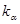 
– -квантиль предельного распределения (2.26)
.
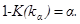Тогда гипотеза о том, что выборка (2.17) взята из распределения с функцией 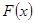, принимается, если 
, и отвергается, если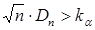 
. Уровень значимости этого критерия приближенно равен .
С той же самой предельной функцией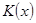 
связан критерий Смирнова. Он состоит в следующем. Пусть 
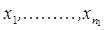и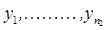 
- две независимые выборки, первая имеет функцию распределения 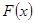, вторая - 
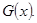Обозначим:
.
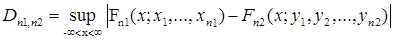Н.В.Смирнов доказал, что если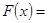 
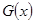непрерывны, то при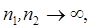 
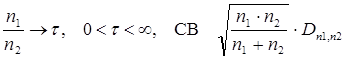в пределе имеет тот же закон распределения 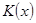, определенный рядом (2.26). Эта предельная теорема позволяет нам строить критерий по проверке гипотезы о том, что выборки 
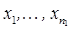и 
взяты из одного и того же распределения.
ОЦЕНКИ ПАРАМЕТРОВ
