Рассмотрим две простые гипотезы: проверяемую 
: 
и конкурирующую: 
: 
. С каждым 
-критерием связаны ошибки двух родов. Ошибка первого рода – отвержение гипотезы , когда она верна; принимая гипотезу , в случае когда верна конкурирующая гипотеза , мы делаем ошибку второго рода.
Обозначим
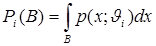, i = 0, 1. (2.1)
Тогда, вероятность ошибки первого рода - критерия равна:
, (2.2)
а вероятность ошибки второго рода равна:
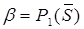, где 
, (2.3)
и 
иногда называют просто ошибками І и ІІ рода.
Задача построения -критерия для проверки простой гипотезы при конкурирующей гипотезе ставится следующим образом. Вероятность ошибки І рода называют уровнем значимости - критерия.
Функцией мощности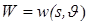 
-критерия называется следующая функция от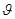 
:
(2.4)
т.е. вероятность отвергнуть гипотезу , если истинное значение параметра равно .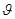
Как видно из (2.2), (2.3) и (2.4), вероятности ошибок І и ІІ рода следующим образом выражаются через функцию мощности:
, 
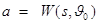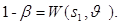
Итак, сначала задается уровень значимости и рассматривается множество 
всех -критериев с уровнем значимости . Среди этих критериев выбирается критерий 
, для которого мощность при 
принимает наибольшее значение, т.е.
, 
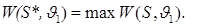
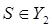
Критерий 
, удовлетворяющий условиям (2.5) называется оптимальным, или наиболее мощным, критерием, который не всегда существует.
Обобщим понятие статистического критерия. Для этого опишем -критерий с помощью функции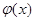 
, определенной по правилу:
(2.6)
Мы можем истолковать 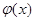, как вероятность отвергнуть гипотезу , когда выборка приобретает значение 
. Критерии, описываемые функцией вида (2.6) называются нерандомизированными. Введем понятие рандомизированого критерия (от англ. random-случайный).
Пусть задана функция 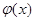, такая, что для любых 
. Мы предполагаем, что с каждыми значением выборки связывается некий случайный эксперимент (рандомизация) с двумя исходами: 1 и 0, причем вероятность 1 равна 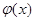, а вероятность 0 равна 
В зависимости от исхода этой рандомизации действует и этот рандомизированный критерий. Если выпала 1, то отвергается, если выпал 0, то принимается.
Функцию мощности этого критерия, который можно назвать 
-критерием обозначим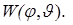 
Она равна:
где 
означает математическое ожидание по распределению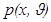 
, а 
- случайная величина, плотность которой равна .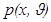
Уровень значимости -критерия равен:
,
а вероятность ошибки II рода равна:
Рассмотрим множество всех -критериев с фиксированным уровнем значимости . Мы будем называть 
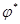-критерий оптимальным или наиболее мощным, если
, 
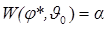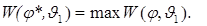(2.7)
Задача (2.7) всегда допускает решения.
