Рассмотрим сначала случай, когда вектор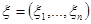 
имеет дискретное распределение
Где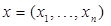 
пробегает конечное или счетное множество возможных значений 
.
Пусть имеется функция 
Условным распределением 
при условии 
назовем совокупность условных вероятностей при фиксированном 
(3.8)
Не более, чем счетное число вероятностей (3.8) отличны от нуля; t выбираем такими, чтобы знаменатель в (3.8) не был равен нулю.
Если 
– числовая функция от векторного аргумента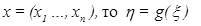 
будет случайной величиной. Ее математическое ожидание равно
Условное математическое ожидание 
определим с помощью условного распределения (3.8):
= 
= 
. (3.9)
Как видно из (3.9), условное математическое ожидание есть функция от . Обозначим ее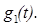 
Подставляя вместо 
случайную величину 
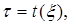мы получаем, что условное математическое ожидание есть случайная величина 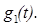Вычислим математическое ожидание от 
= 
.
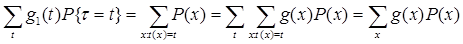Таким образом, мы показали, что
(3.10)
т.е. при вычислении математического ожидания от 
сначала можно вычислить условное математическое ожидание при условии 
а затем усреднить это условное математическое ожидание по вероятностям условий.
Формула (3.10) сохраняет смысл и в том случае, когда ξ имеет не дискретное распределение, а, например, имеет плотность P (x)= P (x 1, …, xn). Пусть плотность 
непрерывна в точке 
, тогда при 
= 
Вычислим условную вероятность
= 
.
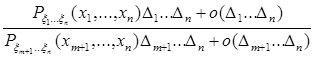Переходя к пределу по ∆i→0, получаем
P{xi<ξi<xi + ∆1, …, xm<ξm<xm + ∆m │ xi<ξi<xi +∆i, i = 
} → 
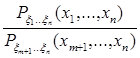, (3.11)
где 
Предел левой части (3.11) называют условной плотностью ξ1,…, ξm при заданных ξm+1,…, ξn:
Математические ожидания
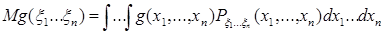
можно вычислять по формуле (3.10), вычислив сначала математическое ожидание
и осредняя его затем по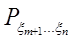 
:
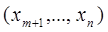(3.12)
Формулу (3.12) можно вывести и в более общем случае. Пусть имеются дифференцируемые функции t1=t1(x), t2=t2(x),…, tm=tm(x). Предположим, что к ним можно подобрать функции yj=yj(x), j=1,…,n-m, такие, что преобразование С, задаваемое функциями
ti=ti(x), i=1,…,m,
yj=yj(x), j=1,…,n-m, (3.13)
взаимно однозначно в соответствующей области. Тогда плотности Рξ(х) и Рτ,η(t,y), где τi = ti(ξ), ηj = yj(ξ), τ=(τ1,…,τm), η=(η1,…, ηn-m), t=(t1,…,tm), y=(y1,…,yn-m), будут связаны равенством
Рξ(х)=Рτ,η(t,y)│J│, (3.14)
где J – якобиан преобразования С. Пусть имеется функция g(ξ1,…, ξn). Вычислим условное математическое ожидание g(ξ1,…, ξn) при условии τ=t. Обозначим xk(t,y)=xk, k=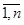 
, x(t,y)= (x1(t,y),…, xn(t,y)) функции, задающие обратное преобразование С -1. Тогда
и
(3.15)
(Здесь мы воспользовались равенством (3.14)).
Достаточные статистики
Определение 1. Пусть ξ=(ξ1,…, ξn) - векторная случайная величина, распределение которой Р(x; 
) зависит от параметра и t(x)=(t1(x),…,tm(x)) - векторная функция (набор m статистик) от х=(х1, …, хn). Мы будем называть t(х) достаточной статистикой, если условное распределение ξ=(ξ1,…, ξn) при условии t(ξ)=t не зависит от параметра .
Мы будем далее иметь в виду два случая: либо Рξ(x; ) - дискретное распределение вероятностей, либо Рξ(x; ) n -мерная плотность и существует взаимно однозначное преобразование С: х=(х1, …, хn) в (t;y), задаваемое формулами (3.13).
Оценки, зависящие только от достаточных статистик, обладают преимуществами по сравнению с другими оценками. Во-первых, они используют не всю информацию, содержащуюся в выборке (3.1), а лишь ту ее часть, которая существенна для оценки параметра. Во-вторых, каждой несмещенной оценке 
с конечной дисперсией соответствует другая несмещенная оценка 
, зависящая от достаточной статистики, с D < D .
Прежде всего, докажем критерий факторизации, позволяющий легко находить достаточные статистики.
Теорема 2. Если распределение Р(x; ) представлено в виде
Р(x; ) =g(t(x); )h(x) (3.16)
то t(х) есть достаточная статистика.
Доказательство. Рассмотрим сначала дискретное распределение Согласно формуле (3.8) условная вероятность ξ=х при условии t(ξ)=t равна
(3.17)
Если выполнено (3.16), то из (3.17) получаем
т.е. t(х) – достаточная статистика.
Если, наоборот, условная вероятность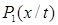 
= 
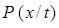не зависит от параметра , то из теоремы умножения вероятностей имеем
Р(x; ) = 
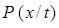
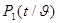
где 
- распределение t, т.е. имеет представление (3.16).
Если Р(x; ) - плотность, то будем предполагать, что имеется преобразование (3.13) и плотности Рξ(x; ) и Pτ,η(t;y; ) связаны соотношением (3.14).
Тогда условная плотность η при условии τ=t, равная
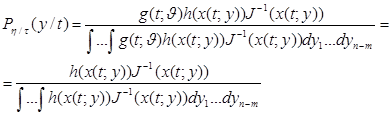
и, следовательно, не зависят от . Так как
не зависит от , то, взяв g(x)= 1 для х 
В и g(х)=0 для х 
В, где В Вn – борелевское множество из Rn, получаем, что Р{ξ 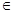B | τ=t} не зависит от при любом В 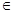Вn, то есть t - достаточная статистика. Пусть наоборот 
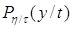не завит от .
Тогда из
и (3.14) имеем
т.е. плотность представлена в виде (3.16).
Теорема 3. (Колмогорова-Блекуэлла)
Пусть t - достаточная статистика семейства распределений Р(x; ), а 
(x) - несмещенная оценка параметра с конечной дисперсией, построенная по выборке (3.1). Тогда условное математическое ожидание при фиксированном t
будет несмещенной оценкой с дисперсией
D 
D .
Доказательство. Из свойства (3.15) имеем
M 
т.е. оценка несмещена ( действительно является оценкой,
так как не зависит от , поскольку - достаточная статистика).
Вычислим D :
D = M ( - )2 = M ( - + - )2 =
= M ( - )2 + M ( - )2 + 2M ( - ) ( - ). (3.18)
Так как
M ( - ) ( - )= M [ M ( - ) ( - )| t ]= M [( - ) M {( - )| t }],
а M {( - )| t }=0, то из (3.18) D 
D . Теорема доказана.
Пример 1. Пусть выборка (3.1) взята из схемы Бернулли (хi= 1, если в i- м испытании был успех, хi =0 в противоположном случае). Параметром в этом случае служить вероятность p. Вероятность появления выборки (3.1) равна
откуда по критерию факторизации следует, что число успехов х1+…+хn есть достаточная статистика.
Пример 2. Пусть (3.1) – независимая выборка из нормального распределения с параметрами (а,ξ). Тогда по критерию факторизации
т.е. 
и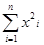 
- достаточные статистики.
Эффективность оценок
Как мы видели в п.3.3, несмещенные оценки параметра с меньшей дисперсией предпочтительней остальных оценок. Естественно поставить вопрос о нахождении оценок с наименьшей дисперсией. Некоторый подход к решению этого вопроса дает неравенство Рао-Крамера. Пусть p(x; )=p(x1,…,xn; ) - плотность, зависящая от параметра , а =φ(x)=φ(x1,…,xn) - оценка параметра по выборке x1,…,xn не обязательно несмещенная. Обозначим g()=M = 
. Предположим, что выполнены некоторые условия регулярности, при которых интегралы
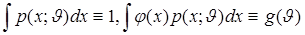
можно дифференцировать по параметру . В этом случае справедливы равенства
(3.19)
(3.20)
Величина, равная математическому ожиданию (здесь ξ имеет распределение P(ξ; ))
(3.21)
называется информацией Фишера относительно семейства p(х; ).
Теорема 4. (Неравенство Рао-Крамера). Если семейство плотностей p(х; ) и оценка = φ(х) таковы, что выполнены условия (3.19) и (3.20), то имеет место неравенство:
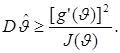(3.22)
Доказательство. Условия (3.19) и (3.20) перепишем в эквивалентном виде:
. (3.23)
Умножим первое из тождеств (3.23) на g () и вычтем его из второго:
(3.24)
Полагая в (3.24) φ1(х)=φ(х)- g (), φ2(х)= 
, применим неравенство Коши-Буняковского
Имеем отсюда:
а это равносильно неравенству (3.22).
Замечание 1. Теорема 4 остается справедливой, если под
p(х; ) понимать вероятности дискретного распределения, а под интегралами – суммы.
Замечание 2. Если тождества (3.19) можно еще раз дифференцировать по :
то информацию Фишера (3.21) можно записать в другом виде:
(3.25)
В самом деле, обозначая 
имеем 
откуда
что и утверждалось.
Замечание 3. Из первого тождества (3.23) следует M 
, поэтому информацию Фишера (3.21) можно записать иначе:
Замечание 4. Если х1,…,хn независимы, то их совместная плотность pn(х1,…,хn; ) есть произведение одномерных плотностей:
pn(х1,…,хn; ) = 
.
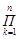
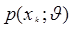В этом случае информация Фишера 
зависит от n линейно:
(3.26)
где 
- информация Фишера одного наблюдения хk, а (3.22) превращается в неравенство следующего вида:
(3.27)
Формула (3.26) следует из
.
Замечание 5. Если оценка 
несмещенная, то 
, и в неравенствах (3.22) и (3.27) числитель равен 
. В условиях теоремы 4 неравенства (3.22) и (3.27) дают оценку снизу дисперсии оценок . Ниоткуда не следует, что эта оценка достигается, однако во многих важных случаях, как мы увидим ниже, она является нижней границей дисперсии хотя бы в асимптотическом смысле при n→∞.
Пример 3. Пусть х1,…,хn - независимая выборка из нормального распределения с параметрами (а, σ), σ - известно. Так как
, 
,
то
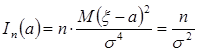
Для оценки 
имеем
т.е. в этом случае в (3.27) достигается равенство.
Ниже мы всегда будем полагать, что условия теоремы 4 выполнены.
Определение 2. Назовем эффективностью оценки отношение
Оценка с эффективностью е()= 1 называется эффективной.
Оценка 
в примере 1 эффективна. Если неравенство в (3.22) или (3.27) для некоторой оценки превращается в равенство, то эффективность оценки - это отношение минимально возможной дисперсии к дисперсии данной оценки:
Эффективность всегда удовлетворяет неравенствам 0≤е()≤1. Конечно, при нарушении условий теоремы 4 равенства (3.22) и (3.27) могут не выполняться и могут существовать “сверхэффективные” оценки с дисперсией D , убывающей при n→∞ быстрее, чем 
.
Пример 4. Пусть х1,….,хn – независимая выборка из распределения с плотностью
В этом случае нарушается условие теоремы (3.19) и оценка
=min xk обладает “сверхэффективностью”, так как
1≤ k<n
.
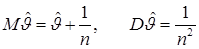Важным понятием в теории статистических оценок является также асимптотическая эффективность. Будем предполагать условия теоремы 4 выполненными.
Определение 3. Асимптотической эффективностью е0( n) оценки n= n(х1,….,хn), построенной по независимой выборке х1,…,хn, назовем предел
если он существует. Оценка n называется асимптотически эффективной, если е0(
n)=1. Таким образом, если - несмещенная оценка с асимптотической эффективностью е0(), то ее дисперсия при больших n асимптотически равна [ е0()·n·J1 
] -1.
Для асимптотически нормальных при n→∞ оценок n полезно другое определение асимптотической эффективности.
Определение 4. Если оценка n при n →∞ асимптотически нормальна с параметрами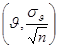 
, то ее асимптотической эффективностью называется отношение:
,
т.е. в этом случае за математическое ожидание и дисперсию оценки мы принимаем математическое ожидание и дисперсию аппроксимирующего нормального закона распределения. Аналогично, если е0()= 1, то оценка будет называться асимптотически эффективной.
Методы нахождения оценок
Метод моментов
Пусть х1,…,хn - независимая выборка из распределения с плотностью р(х; 
), зависящей от r параметров . предположим, что все моменты
конечны, и что система уравнений
,
однозначно разрешима, причем её решение
,
выражается при помощи непрерывных обратных функций 
.
При этих условиях имеет место
Теорема 5. Оценки 
, получаемые как решение системы:
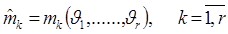, (3.28)
где
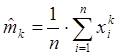- выборочные моменты, состоятельны.
Доказательство. Согласно нашим предположениям, система (3.28) имеет единственное решение:
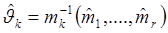
причем 
- непрерывные функции. По усиленному закону больших чисел 
сходятся п.н. к mk , а из непрерывности функций отсюда следует, что k при n→∞ п.н. (почти наверное, т.е. с вероятностью, равной 1) сходятся к 
.
Метод моментов дает состоятельные оценки, но часто их эффективность и асимптотическая эффективность меньше 1.
