путем аналогичных преобразований условного товарооборота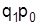 
из тождественного агрегатного индекса
через соответствующие индивидуальные индексы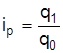 
. Поскольку 
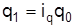, то 
.
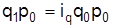Абсолютное изменение индексированной величины определяется по схеме, аналогичной схеме агрегатных индексов.
Пример расчета средневзвешенных индексов цен и количества проданных акций на фондовом рынке приведен в табл. 8.2.
Таблица 8.2
| Рынок | Объем торгов, млн. грн. | Темп прироста, % |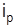 
| 
| ||
базисный период
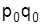
| текущий период
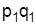
| цен на акции | количества акций | |||
| Первичный | +90 | +35 | 1,9 | 1,35 | ||
| Вторичный | +150 | +20 | 2,5 | 1,20 | ||
| Всего | Х | Х | Х | Х |
Средневзвешенный индекс цен составляет:
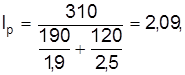
следовательно, в целом по фондовому рынку цены на акции в текущем периоде по сравнению с базисным выросли в среднем в 2,09 раза.
Средневзвешенный индекс количества проданных акций равняется:
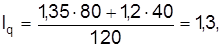
поэтому количество проданных акций в среднем возросло на 30%.
Индексы средних величин 
характеризуют относительное изменение среднего значения показателя х.
Уровень средней зависит от значений признака хи соотношения весов:
,
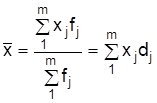где fj – частота; dj – доля j-й составляющей совокупности.
Соответственно динамика средней определяется изменением значений xjи структурными сдвигами dj. Оценка воздействия каждого из факторов осуществляется в рамках системы индексов средних величин: переменного состава, фиксированного состава и структурных сдвигов.
Индекс переменного состава характеризует относительное изменение средней величины в целом за счет обоих факторов: признака xj и структуры совокупности dj.
.
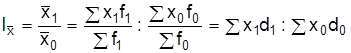Индекс фиксированного состава Ixпоказывает изменение средней величины за счет изменения только значений признака при неизменной структуре совокупности:
.
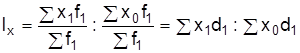Индекс структурных сдвигов Idпоказывает изменение средней за счет сдвигов в структуре совокупности:
.
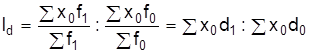Формулы индексов фиксированного состава и структурных сдвигов разновзвешенные. В Ix веса фиксируются на уровне текущего периода, а в Idзначение признака х – на уровне базисного периода. Такой принцип взвешивания обеспечивает увязку трех индексов в систему:
.
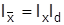Пример. Определим индексы среднего размера страхового тарифа при страховании легковых автомобилей со сроком эксплуатации до 3 лет (табл. 8.3).
Таблица 8.3
| Автомобиль | Страховой тариф, % | Страховая сумма, тыс. грн. | Сумма страхового возмещения, тыс. грн. | ||||
| базисный период x0 | текущий период x1 | базисный период f0 | текущий период f0 | x0f0 | x1f1 | x0f1 | |
| Отечественный | 2,5 | 3,0 | 13,0 | 22,5 | 18,75 | ||
| Зарубежный | 5,0 | 6,0 | 19,0 | 51,0 | 42,50 | ||
| Всего | -- | -- | 32,0 | 73,5 | 61,25 |
Индекс переменного состава составляет
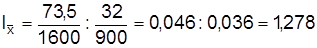
и показывает, что средний страховой тариф в текущем периоде по сравнению с базисным повысился на 27,8%. Индекс фиксированного состава
,
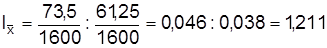т.е. за счет повышения страхового тарифа по каждой группе автомобилей средний страховой тариф увеличился на 21,1%. Индекс структурных сдвигов составляет: Id=0,038:0,036=1,056, следовательно, средний страховой тариф увеличился на 5,6% за счет изменения в составе объектов страхования, а именно – увеличения доли страховой суммы зарубежных автомобилей с более высокой страховой ставкой.
Взаимосвязь взаимозависимых индексов обеспечивается:
=1,211 •1,056=1,278.
Разновидностью индексов средних величин являются территориальные индексы, в которых средние уровни сравниваются по отдельным территориям, объектам.
Для построения территориальных индексов необходимо обосновать базу сравнения и порядок фиксации в пространстве значений признака хjи структуры совокупности dj. База сравнения может быть разной или одинаковой. Разная база, т.е. по каждому объекту "своя", выбирается произвольно, в зависимости от цели сравнения. Одинаковой базой может быть средняя или стандартная для двух объектов, например, при сравнении смертности населения отдельных стран за стандарт берется европейская структура населения по возрасту. Средняя база для значений признака xj определяется как средняя арифметическая взвешенная по двум объектам, а средняя структура – как структура суммарной двух объектов совокупности.
Территориальный индекс переменного состава по объектам А и В вычисляется по формуле
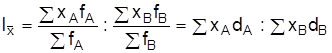
и показывает, в сколько раз средний уровень признака объекта А больше или меньше, чем объекта В.
Территориальный индекс фиксированного состава:
,
где fst – частота; dst – доля стандартной структуры совокупности. Вместо стандартной структуры совокупности может использоваться средняя структура. Ixпоказывает соотношение средних значений признака при фиксированной структуре совокупности.
Пример. Расчет территориальных индексов средней ожидаемой продолжительности жизни населения двух стран показан в табл. 8.4.
Таблица 8.4
| Группа населения | Средняя ожидаемая продолжительность жизни, лет | Структура населения по полу, % | |||
| страна А xA | страна В xB | страна А dA | страна В dB | стандартная dst | |
| Мужчины | |||||
| Женщины | |||||
| Всего | Х | Х |
Территориальный индекс переменного состава составляет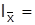 
(72*0,46+78*0,54):(62*0,52+65*0,48)=75,24:63,44=1,186. Следовательно, средняя ожидаемая продолжительность жизни населения страны А в 1,186 раза больше, чем в стране В.
Индекс фиксированного состава за стандартной структурой составляет:
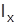= (72*0,49+78*0,51):(62*0,49+65*0,51)=75,06:63,53 =1,181.
Т.е., при условиях стандартной структуры населения в обеих странах средняя ожидаемая продолжительность жизни в стране А превышает уровень страны В на 18,1%.
