Основные требования к методике построения статистических графиков:
1). В график по возможности следует включать исходные данные к его построению. Если это нецелесообразно, то исходные данные должны в табличной форме сопровождать график.
2). Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко было отсчитывать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс.
3). Факторные признаки должны размещаться на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки – по вертикальной шкале и читаются снизу вверх.
При всем своем разнообразии статистические графики классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач.
По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы.
Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. В статистике коммерческой деятельности рынке товаров и услуг наибольшее применение имеют линейные диаграммы. Для их построения обычно применяется система прямоугольных координат. На оси абсцисс откладываются варианты изучаемого показателя (или показания времени), а по оси ординат — величина изучаемого показателя. По отметкам (точкам) обеих осей координат определяется положение каждого уровня на поле графика. Последовательно соединяя точки отрезками линий, получают эмпирическую линию графика, так называемую статистическую кривую. По виду этой линии можно судить о характере развития изучаемого явления в пространстве или во времени.
Важным достоинством линейных графиков является то, что на одном и том же поле графика можно изобразить несколько показателей, что позволяет сравнивать и выявлять специфику их развития во времени или характер изменения одного показателя по разным объектам в пространстве или территории. При этом следует учитывать, что каждую кривую надо изображать отдельной формой линии (сплошная, пунктирная и т. д.) или окрашивать разными цветами.
Другим часто используемым в статистике коммерческой деятельности методом наглядного изображения статистической информации являются столбиковые диаграммы.
При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система координат. При этом каждое значение изучаемого показателя изображается в виде вертикального столбика. По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для всех столбиков. Высота столбиков (в соответствии с принятым по оси ординат масштабом) должна строго соответствовать изображаемым данным.
В статистике коммерческой деятельности находят применение так называемые ленточные (полосовые) графики В этих диаграммах основания столбиков располагаются вертикально, а масштабная шкала наносится на горизонтальную ось. По своей форме ленточная диаграмма представляет ряд простирающихся по оси абсцисс полос одинаковой ширины. Длина полос (лент) соответствует значениям изображаемых показателей При построении ленточных диаграмм соблюдаются те же требования, что и при построении столбиковых графиков (одинаковая ширина полос, начало масштабной шкалы от нулевой отметки и др).
Линейные, столбиковые и полосовые диаграммы имеют широкое применение в изображении статистической информации о коммерческой деятельности на рынке товаров и услуг При этом линейным и столбиковым диаграммам отдается предпочтение, если в изучаемых показателях проявляется общая тенденция роста. Горизонтальные ленты (полосы) нагляднее, если изображаемые показатели отображают результат (итог) функционирования того или иного процесса.
Широкое применение в статистике коммерческой деятельности находят круговые диаграммы. В этих диаграммах площадь окружности принимается за величину всей изучаемой статистической совокупности, а площади отдельных секторов отображают удельный вес (долю) ее составных частей. При этом поскольку площади секторов пропорциональны их центральным углам, то для построения секторной диаграммы сумма всех углов (360°) распределяется пропорционально удельным весам отдельных частей изучаемой совокупности.
Интервальный ряд распределения изображается графически в виде гистограммы.. При ее построении на оси абсцисс откладывают интервалы ряда, высота которых равна частотам, отложенным на оси ординат. Над осью абсцисс строятся прямоугольники, площадь которых соответствует величинам произведений интервалов на их частоты.
В практике экономической работы возникает потребность в преобразовании рядов распределения в кумулятивные ряды, строящиеся по накопленным частотам. С их помощью можно определить структурные средние, прослеживать за процессом концентрации изучаемого явления. Они облегчают анализ данных ряда распределения.
Накопленные частоты определяются путем последовательного прибавления к частотам (или частостям) первой группы этих показателей последующих групп ряда распределения. Используя данные накопленного ряда, строят график в виде кумуляты (кривой сумм).
При графическом изображении кумуляты накопленные частоты наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Длина этих линий равна величине накопленных частот в конкретном интервале. Соединяя затем эти перпендикуляры, получаем ломаную линию, от начала ряда до той точки, которая равна объему данной совокупности, т. е. сумме частот ряда.
Тема 4. Средние величины
Основные понятия
Средняя величина – это обобщающая мера варьирующего признака, которая характеризует ее уровень в расчете на единицу совокупности. Условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой её объем.
В статистической практике используют несколько видов средних: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратичная и т. д. Каждая из указанных средних может приобретать две формы: простую и взвешенную. Если средняя вычисляется по первичным (не сгруппированным) данным, применяется простая форма, если по вторичным (сгруппированным) – взвешенная.
Использование каждого вида средних зависит от двух обстоятельств, во-первых, от характера индивидуальных значений признака (прямые, обратные, квадратичные, относительные). Во-вторых, от характера алгебраической связи между индивидуальными значениями признака и общим объемом (сумма, произведение, степень, квадратичный корень). Эта связь является определяющим свойством совокупности и отражается в логической формуле усредняемого признака. На основании логической формулы выбирается вид средней.
Средняя арифметическая –используется для усреднения прямых значений признаков путем их суммирования. Ее логическая формула имеет вид
 .
.
Если данные несгруппированные, используется средняя арифметическая простая
 ,
,
где x i – отдельные значения признака,
n – объем совокупности.
Пример. Уставный фонд акционерной компании сформирован 6 учредителями; размер взноса каждого из них составляет, млн. грн.: 6; 10; 12; 9; 7; 4. Средний взнос одного учредителя

По формуле средней арифметической простой вычисляются также средние в хронологическом ряде, если интервалы времени, за которые даются значения признаков, одинаковые.
Пример. Квартальный оборот универсальных бирж в течение года составлял, млн. грн.: І кв. – 372; II кв. – 423; III кв. – 340; IV кв. – 455. Среднеквартальный оборот бирж составляет

Если в хронологическому ряду приведены моментные показатели, то для вычисления средней они заменяются полусуммами значений на начало и конец периода. Если моментов больше двух и интервалы между ними одинаковые, то средняя вычисляется по формуле средней хронологической
 ,
,
где n –число моментов.
Пример. В коммерческом банке сумма кредиторской задолженности на начало каждого квартала составляла, млн. грн.: 01.01 – 20; 01.04 – 26; 01.07 – 32; 01.10 – 29; 01.01 следующего года – 22. Среднеквартальная сумма кредиторской задолженности

Если данные сгруппированы, то используют средневзвешенную арифметическую
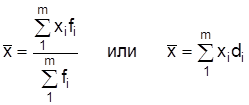 ,
,
где fi – частота;
di – частость i-й группы (удельный вес).
При этом  .
.
Так, по результатам сдачи экзамена студентами группы (табл. 4.1), средний балл оценок составляет 3,8.
Таблица 4.1
| Оценка знаний студентов, баллов | xi | Всего | ||||
| Количество оценок | fi | |||||
| Удельный вес оценок, % | di | 26,7 | 40,0 | 20,0 | 13,3 |
На основании частот
 ,
,
на основании частостей
 .
.
Усреднению подлежат не только отдельные значения вариант, но и их групповые средние  , тогда весом будет частота (частость) каждой группы:
, тогда весом будет частота (частость) каждой группы:
 .
.
Вычисленная таким способом средняя из групповых средних называется общей.
Весом может быть также абсолютная величина, которая логично связана с усредняемым показателем. Выбор весов основывается на логической формуле показателя. Поскольку средняя величина вычисляется в расчете на единицу совокупности, то вес всегда будет находиться в знаменателе логической формулы. Например, при определении средней суммы расходов на одно рекламное сообщение весом будет количество рекламных сообщений. При вычислении средней суммы расходов на одного рекламодателя весом будет количество рекламодателей.
Средняя арифметическая имеет определенные математические свойства, которые раскрывают ее суть. Так, сумма отклонений отдельных вариант от средней равна нулю, а сумма квадратов таких отклонений приближается к минимуму. Эти два свойства положены в основу изучения вариации признаков.
Если отдельные значения вариант увеличить (уменьшить) на величину А или в kраз, то средняя изменится соответственно.
Например, если денежные взносы граждан в Сбербанк откорректировать на уровень инфляции, что составляет 1,2, то средний размер взноса увеличится соответственно в 1,2 раза.
Средняя не изменится при пропорциональном изменении всех весов, но ее размер претерпевает изменения при определенных структурных сдвигах.
Например, при неизменной курсовой стоимости акций отдельных эмитентов средняя стоимость акций может повыситься за счет увеличения доли "дорогих" акций в общем количестве их продаж.
Отмеченные свойства средней используют в случае усреднения признаков порядковой (ранговой) шкалы. Варианты признака можно оцифровать порядковыми рангами Ri = 1, 2,..., n или центрированными R0 = -2, -1, 0, 1, 2 (табл. 4.2). Очевидно, что  . Средний центрируемый бал отклоняется от среднего порядкового на величину
. Средний центрируемый бал отклоняется от среднего порядкового на величину  .
.
Средний центрируемый балл приобретает положительные или отрицательные значения и свидетельствует о позитивной или негативной оценке явления. Кроме того, его используют для сравнения оценок различных явлений, поскольку он не зависит от размерности шкалы.
Поприведенными в табл. 4.2 данным об отношении населения к приватизации земли,
 ;
;
 .
.
Следовательно, уровень поддержки приватизации земли позитивный, но пока что невысокий.
Таблица 4.2
| Отношение к приватизации | Частота ответов, % | Ранги | |
| Ri | R0 | ||
| Полностью поддерживаю | |||
| Частично поддерживаю | |||
| Не поддерживаю | - 1 | ||
| Всего | - | - |






