.
Если данные сгруппированы, то используют среднюю гармоническую взвешенную
.
Очевидно, что среднюю гармоническую взвешенную целесообразно использовать, когда отсутствует информация о значении знаменателя логической формулы, т.е. отсутствуют веса.
Пример. Окупаемость расходов на развитие новаторских работ характеризуется данными табл. 4.3.
Таблица 4.3
| Новаторские работы | Доход от использования, млн. грн. | Окупаемость 1 млн. расходов на развитие новаторства, млн. грн. |
| Изобретения | 4,6 | |
| Рационализаторские предложения | 6,5 | |
| Всего | -- |
Логическая формула окупаемости расходов на развитие новаторства будет иметь вид
.
Поскольку в роли веса fi выступают расходы на развитие работ, которые в таблице отсутствуют, то применяется средняя гармоническая
Рассчитывать среднюю можно и в том случае, когда отдельные значения вариантов не указаны, а известны только итоги (суммарные значения числителя и знаменателя) логической формулы.
Пример. Общий размер капитала пяти самых влиятельных коммерческих банков составлял 318,8 млн. грн., а общая сумма прибыли – 51,7 млн. грн. Средняя прибыльность капитала будет определяться по логической формуле
.
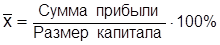Отсюда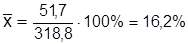 
.
Средняя геометрическая определяется как произведение относительных величин динамики xi, которые являются кратными соотношению i-го значения показателя к предыдущему (i –1). Формула средней геометрической простой
,
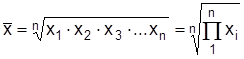где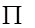 
– символ произведения;
n – число усредняемых величин.
Пример. Количество зарегистрированных преступлений за четыре года выросло в 1,57 раза, в том числе за первый год – в 1,08, за второй – в 1,1, за третий – в 1,18, за четвертый – в 1,12 раза. Среднегодовой темп роста количества зарегистрированных преступлений составляет
,
т.е. число зарегистрированных преступлений росло ежегодно в среднем на 12%.
Если часовые интервалы неодинаковые, используют среднюю геометрическую взвешенную
,
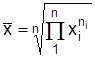где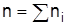 
– часовой интервал.
Средняя квадратичная рассматривается как характеристика вариации (тема 5).
Социально-экономические явления чрезвычайно сложные и многогранные. Любой показатель отражает только одну грань предмета познания. Комплексная характеристика последнего предусматривает использование системы показателей. Каждый показатель системы имеет самостоятельный смысл и в то же время является составляющей обобщающего свойства, которая дает основания для конструирования интегральных оценок явлений. Поскольку показатели системы, как правило, разноименные, то объединение их в интегральную оценку предусматривает стандартизацию – приведение к одному виду. При стандартизации индивидуальные значения показателей заменяются рангами, баллами, относительными величинами, стандартными отклонениями и тому подобное.
Так, рейтинговая оценка финансового состояния банков интегрирует пять параметров деятельности: качество капитала, качество активов, банковский менеджмент, прибыльность, ликвидность. Каждый параметр оценивается баллами – от 1 (сильный) до 5 (неудовлетворительный). Средний невзвешенный балл выступает как рейтинговая оценка финансового состояния банка. Если оценка качества капитала 3 балла, активов – 4, менеджмента – 3, прибыльности – 2 и ликвидности – 3, то средний балл составляет 15:5=3, т.е. финансовое состояние банка посредственное.
При стандартизации при помощи относительных величин базой сравнения может быть или эталонное значение (норма, стандарт) или среднее значение показателя по совокупности:
,
где xi j – значение і-го показателя j-го элемента совокупности;
xi, st – эталонное значение этого показателя;
– среднее.
Среди показателей системы выделяются стимуляторы и дестимуляторы. Показатели-стимуляторы свидетельствуют о высоком уровне i-го показателя при pi j > 1; дестимуляторы – при pi j < 1. Чтобы привести их к однозначной характеристике, для дестимуляторов pi jвычисляется как обратная величина.
Средняя величина относительных m признаков, т.е. многомерная средняя, является интегральной оценкой j–го элемента совокупности:
.
Если показатели системы считаются неравновесными, каждому из них присваивается определенный вес di, а расчет многомерной средней ведется по формуле арифметической взвешенной:
.
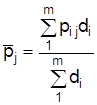При 
уровень явления j-го элемента выше среднего в совокупности или нормативного; при 
, наоборот, ниже.
В табл. 4.4 приведен расчет многомерной средней для оценки инвестиционной привлекательности j-го предприятия-эмитента. Показатели считаются равновесными, первые два – стимуляторы, третий и четвертый – дестимуляторы.
Многомерная средняя составляет 
, т.е. финансовое состояние эмитента можно считать привлекательным для инвесторов.
Таблица 4.4
| Показатель | Уровень показателя xi j | Норматив xi, st | Pi j |
| Рентабельность активов, % | 47,20 | 20,00 | 2,36 |
| Оборотность активов, | 0,80 | 0,67 | 1,19 |
| Коэффициент капитализации, % | 3,90 | <10,0 | 2,56 |
| Коэффициент задолженности | 0,34 | 0,70 | 2,06 |
| Всего | -- | -- | 8,17 |
