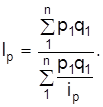Основные понятия
Динамический ряд – это размещенные в хронологической последовательности значения определенного статистического показателя. Составляющими динамичного ряда являются признак времени t(момент или интервал) и числовые значения показателя – уровни yt. В соответствиис классификацией показателей по признаку времени динамичные ряды делят на моментные и интервальные. Вмоментных рядах уровни фиксируют состояние явления на определенные моменты времени, винтервальных – агрегированный результат за определенный промежуток времени. Примеры указанных рядов динамики приведены в табл. 7.1: где поквартальные объемы экспорта товаров – это интервальный ряд, а суммы резервов иностранной валюты на конец квартала – моментный ряд
Таблица 7.1.
| Год, квартал | Объем экспорта товаров в ценах ФОБ, млн. дол. США | Сумма резервов иностранной валюты на конец квартала, млн. дол. США |
| 1998 IV | – | 4,7 |
| 1999 I | 2,8 | 6,3 |
| II | 3,5 | 14,1 |
| III | 3,9 | 9,9 |
| IV | 4,2 | 9,1 |
Уровни динамичных рядов меняются, варьируют. Обобщающей их характеристикой есть средний уровень, который в интервальном ряду рассчитывается по формуле средней арифметической простой, а в моментном – по формуле средней хронологической. По данным табл. 7.1 среднеквартальный объем экспорта товаров составлял
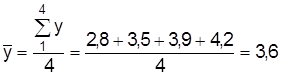млн. долл. США,
а среднеквартальный резерв иностранной валюты
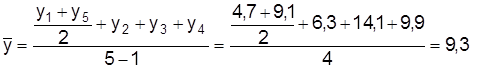млн. долл. США.
Изучая особенности развития социально-экономических явлений, определяют абсолютные и относительные характеристики динамики: абсолютный прирост и абсолютное значение 1% прироста; темп роста (индекс) и темп прироста. Расчет их основывается на сравнении уровней динамичного ряда. Если база сравнения постоянная, характеристики динамики называют базисными, если база сравнения переменная, в качестве которой используют предшествующий уровень – цепными.
Абсолютный прирост (уменьшение)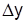 
– это разница уровней динамичного ряда
цепные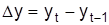 
, базисные 
.
Очевидно, что сумма цепных абсолютных приростов равно конечному базисному:
.
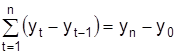Темп роста Tpрассчитывается как отношение уровней ряда; выражается коэффициентом или процентом:
цепные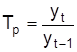 
, базисные 
.
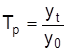Произведение цепных Tp равно конечному базисному:
.
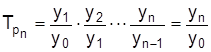Темп прироста Тпрпоказывает, на сколько процентов уровень ytбольше (меньше) уровня, взятого за базу сравнения. Его можно определить как отношение абсолютного прироста к базе сравнения или непосредственно на основании темпа роста. Так, для цепных характеристик:
.
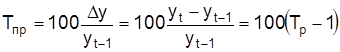Аналогично взаимосвязаны и базисные характеристики динамики.
Абсолютное значение 1% прироста показывает, чего стоит один процент; рассчитывается как отношение абсолютного прироста и темпа прироста. Алгебраическое это отношение равно 0,01 уровня, взятого за базу сравнения:
.
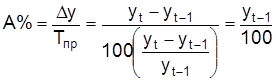Для базисных темпов прироста значения А%одинаковые.
Порядок расчета характеристик динамики рассмотрим на примере объема экспорта товаров (табл. 7.2).
За II–IV кварталы экспорт товаров из региона увеличился на 1,4 млн. долл. США, или на 50% по сравнению с І кварталом. Поквартальные абсолютные приросты и темп прироста уменьшались, однако абсолютное значение 1%прироста росло.
Таблица 7.2.
| Квартал | Объем экспорта, млн. долл. США | Абсолютный прирост, млн. дол. США | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, тыс. дол. США | |||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| І | 2,8 | -- | -- | -- | -- | -- | ||
| ІІ | 3,5 | 0,7 | 0,7 | |||||
| ІІІ | 3,9 | 0,4 | 1,1 | |||||
| IV | 4,2 | 0,3 | 1,4 |
Обобщающими характеристиками интенсивности динамики являются средний абсолютный прирост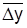 
и средний темп роста 
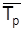. Средний абсолютный прирост рассчитывается как средняя арифметическая простая цепных абсолютных приростов:
.
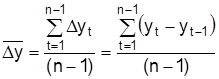Средний темп роста рассчитывают по формуле средней геометрической:
.
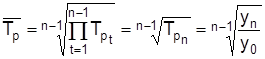По данным табл. 7.2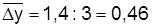 
млн. долл. США, 
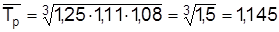, т.е. ежеквартально объем экспорта рос в среднем на 460 тыс. долл. США, или на 14,5%.
Если абсолютная или относительная скорость динамики в границах изучаемого периода неодинакова, сравнением одноименных характеристик за различные интервалы времени измеряется ускорение (замедление) динамики. Разница абсолютных цепных приростов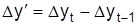 
характеризует абсолютное ускорение (+) или замедление (-) динамики. Для положительных абсолютных приростов можно определить относительное ускорение (
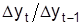). Если интервалы времени неодинаковые, используют средние абсолютные приросты соответствующих интервалов.
На основании темпов роста (базисных или средних) проводят сравнительный анализ интенсивности динамики параллельных рядов, например, грузооборота железнодорожного и автомобильного транспорта. Соотношение темпов роста типа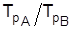 
называют коэффициентом опережения.
Если ряды динамики взаимосвязаны, т.е. их уровни представляют фактор хи результат y, из соотношения темпов прироста этих признаков определяют, на сколько процентов меняется yс изменением х на 1%. По содержанию отношение темпов прироста является коэффициентом эластичности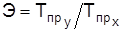 
. Например, цены на товар выросли на 5%, а спрос уменьшился на 3%. Темпы прироста цен и снижения спроса составляют, соответственно, 
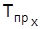= -3%, 
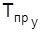= +5%. Следовательно, 
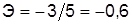, т.е. с ростом цен на 1% спрос уменьшается на 0,6%.
Предпосылкой анализа динамичных рядов является сравнимость данных, которая обеспечивается на этапах их сбора и обработки. Однако возможна ситуация, когда через изменение в методологии расчета показателя, структурные или территориальные сдвиги, изменение цен и тому подобное данные окажутся несравнимыми. Тогда используют специальные приемы соединения прерывистых рядов – "статистические ключи". Например, имеем прерывистый ряд:
| Период | |||
| Уровень ряда: | |||
| до изменений | -- | ||
| после изменений | -- | 22,5 |
Преодолеть прерывистость такого ряда можно двумя способами:
а) скорректировав одну из частей ряда на отношение уровней во 2-м периоде, например, 12•18/15= =12•1,2=14,4;
б) для каждой части ряда определить базисные темпы роста, приняв уровень 2-го периода за базу сравнения, т.е.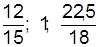 
.
Тенденция – это основное направление развития. В рядах с четко определенной тенденцией ее описывают аналитически при помощи определенной функции:
,
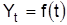где t = 0, 1, 2,..,. n – переменная времени; Yt – теоретические уровни ряда.
Указанную функцию называют трендовым равенством. Выбор функционального вида тренда зависит от характера динамики. Так, при относительно стабильных абсолютных приростах используют линейный тренд Yt=a+bt, при стабильных темпах прироста – показательную функцию Yt=abt ит.д. Соответственно параметр b влинейной функции характеризует средний абсолютный прирост, в показательной – средний темп роста. Параметр а вобеих функциях – это теоретическое значение уровня при t=0.
Рассчитываются параметры уравнений тренда методом наименьших квадратов, при этом нелинейные функции приводятся к линейному виду, например, логарифмированием lgYt = lga + t lgb. Система нормальных уравнений имеет вид:
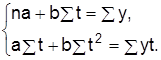
Если начало отсчета времени (t=0)перенести в середину ряда, то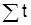 
=0, а следовательно,
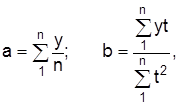
где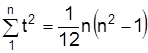 
.
Пример. Расчет линейного тренда показан в табл. 7.3 на примере экспорта сахара. По данным таблицы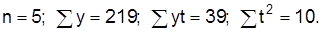 
Таблица 7.3
| Год | Экспорт сахара, тыс. т yt | t | tyt | Yt | yt-Yt | (yt-Yt)2 |
| - 2 | - 74 | 36,0 | - 1,0 | 1,00 | ||
| - 1 | - 39 | 39,9 | - 0,9 | 0,81 | ||
| 43,8 | - 0,8 | 0,64 | ||||
| 47,7 | 0,3 | 0,09 | ||||
| 51,6 | 0,4 | 0,16 | ||||
| Всего | -- | 2,70 |
Параметры уравнения тренда составляют:
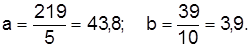
Следовательно, Yt=43,8+3,9 t, т.е. средний уровень экспорта сахара составлял 43,8 тыс. т. Ежегодно экспорт сахара растет в среднем на 3,9 тыс. т. При условии, что комплекс причин, который формирует тенденцию, вскоре не изменится, можно продолжить тенденцию за границы динамичного ряда (экстраполировать тренд). Ожидаемый объем экспорта сахара в 1997 г. (t=3) составляет:
Y1997=43,8+3,9•3=55,5 или Y1997=51,6+3,9=55,5 тыс.т.
Это точечная оценка прогноза. Интервальная оценка прогноза, т.е. доверительные границы, определяется с определенной вероятностью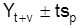 
, где sp – погрешность прогноза;
t – доверительное число для принятого уровня вероятности;
v – период прогнозирования.
Погрешность прогноза spрассчитывается по формуле:
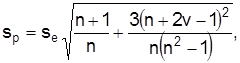
где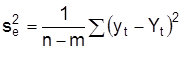 
– оценка остаточной дисперсии.
По данным табл. 7.3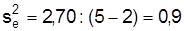 
, а следовательно, 
.
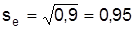Подкоренное выражение равно 2,1, а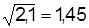 
. Критическое значение двухстороннего t-критерия для а=0,05и числа степеней свободы (n-2)=5-2=3 составляет t0,95(3)=2,57 (Приложение).
Таким образом, sp=2,57•0,95•1,45=3,5, а доверительные границы прогнозного уровня 55,5±3,5.
Если в ряду динамики тенденция четко не проявляется, то прибегают к сглаживанию ряда. Суть его заключается в укрупнении интервалов времени и замене уровней первичного ряда средними по интервалам. Интервалы длиной mможно сформировать двояко:
а) последовательно, например, при m=3 уровни объединяются: 1-3, 4-6 и т.д; рассчитанные средние называют ступенчатыми;
б) скользящим способом, когда первый уровень i-го интервала заменяется следующим уровнем за границами интервала, например, 1-3, 2-4, 3-5 и т.д. Интервальные средние называют скользящими. Очевидно, что ряд скользящих средних короче первичного ряда на (m-1).
Для оценки вариации уровней динамичного ряда используют абсолютную меру – среднее квадратичное отклонение sp и относительную меру – коэффициент вариации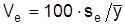 
. Поданным табл. 7.3, se=0,95, Ve=100•0,95/43,8=2,2%. Разницу 100-Ve используют для оценки постоянства динамичного ряда.
Разновидностью колебаний динамичных рядов являются сезонные колебания, т.е. более-менее устоявшиеся колебания по месяцам или кварталам года. При изучении сезонных колебаний используют относительные величины – индексы сезонности Ic. При отсутствии тенденции Icрассчитываются как отношение фактических уровней ytк среднему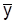 
, т.е. 
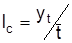. При наличии тенденции базой сравнения служат теоретические уровни Yt, т.е. Ic=yt/Yt.
Таблица 7.4.
| Месяц | Зарегистрировано браков | Ic | Ic-100 | (Ic-100)2 |
| Январь | - 3 | |||
| Февраль | -4 | |||
| Март | - 16 | |||
| Апрель | - 5 | |||
| Май | - 19 | |||
| Июнь | ||||
| Июль | ||||
| Август | ||||
| Сентябрь | ||||
| Октябрь | ||||
| Ноябрь | ||||
| Декабрь | - 2 | |||
| Всего | -- |
Пример. Анализ сезонной волны представлен в табл. 7.4 на примере числа зарегистрированных браков. Первичный ряд динамики не выявляет четкой тенденции, а поэтому индексы сезонности рассчитываются на основании постоянной средней.
Абсолютной мерой сезонных колебаний является амплитуда колебаний R=Imax-Imin. Поданным табл. 7.4 R=122-81=41. Для сравнения интенсивности сезонных колебаний используют также среднее линейное отклонение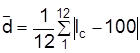 
или среднее квадратичное 
.
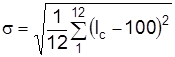По данным табл. 7.4 среднее квадратичное отклонение составляет 
пункта.
Для характеристики закономерных колебаний в рядах динамики с меньшими интервалами времени (декада, пятидневка, сутки) вычисляют коэффициенты неравномерности: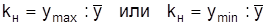 
.
Тема 8. Индексы
Основные понятия и категории
Индекс – это относительная величина, которая характеризует изменение явления во времени, пространстве или степень отклонения от стандарта.
Как относительная величина индекс выражается в форме коэффициента, процента или промилле. Название индекса отражает его социально-экономическое содержание, а числовое значение – интенсивность изменения или степень отклонения. Например, региональный индекс преступности – 1,47, а отраслевой индекс производительности труда – 0,96.
Индексы выполняют две функции: синтетическую – это обобщающая характеристика изменения явления; аналитическую – изучение воздействия отдельных факторов на изменение явления. Большинство индексов выполняет обе функции одновременно.
В зависимости от цели сравнения индексы делятся на: динамичные – характеризуют изменение явления во времени; территориальные – отражают результат сравнения явления в пространстве (по различным объектам, регионам), межгрупповые – характеризуют отклонение от стандарта (эталонного, минимального, максимального) или от среднего уровня. Например, индекс превышения смертности мужчин по сравнению с женщинами.
В зависимости от вида величины, которая индексируется, различают индексы абсолютных и средних величин. По степени агрегированности информации индексы делят на индивидуальные и сводные. Индивидуальные индексы характеризуют соотношения уровней показателя для отдельных элементов совокупности или однородных групп, сводные – для определенного множества элементов. Основой построения сводных индексов является обобщение информации путем ее агрегирования (агрегатные индексы) или осреднения (средневзвешенные индексы). В структурируемой совокупности индексы могут быть групповыми (субиндексами) илиобщими. Например, индексы динамики заболеваемости по отдельным инфекционным болезням являются субиндексами, а динамики заболеваемости по инфекционным болезням в целом – общим индексом.
Показатель, который сравнивается во времени или пространстве, называют индексированной величиной. В международной статистике используют такую систему обозначений индексированных величин: р – цена; q – физический объем, а именно количество товаров, продукции и тому подобное; с – себестоимость единицы продукции; t – трудоемкость работы или производства продукции.
В динамичных индексах предыдущее значение величины, которое принимается за базу сравнения, обозначается подстрочной отметкой "0", а текущее, оценочное значение – "1". В территориальных индексах база сравнения произвольная. Например, индивидуальный индекс динамики цен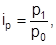 
а территориальный индекс количества проданных товаров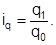 
Предпосылкой расчета индивидуальных индексов есть сопоставимость измерения числителя и знаменателя. При агрегировании совокупности элементов, которые имеют различные единицы измерения, их физические объемы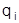 
приводят к сравнимому виду посредством определенных соизмерителей. Используют соизмерителистоимостного характера (цена, себестоимость), тогда агрегатом будет 
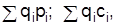или трудового (трудоемкость) – агрегат принимает вид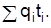 
В агрегированных данных индексироваться могут: отдельно соизмерители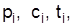 
отдельно "веса" 
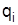или агрегат в целом. Если индексируется соизмеритель, то весы фиксируют на неизменном уровне (базисном или текущем). Так же фиксируется соизмеритель, если меняются веса. Используют две равноправных индексных системы:
| базисно-взвешенную (Ласпереса) | текуще-взвешенную (Пааше) | |
| индекс цен |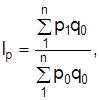 
| 
|
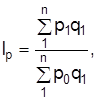
| индекс физического объема |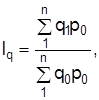 
| 
|
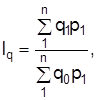
Относительное изменение агрегата в целом оценивается сводным индексом стоимости товаров (товарооборота)
Принимая во внимание мультипликативную связь между соизмерителем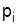 
и весами 
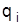, указанные индексы связываются в систему:
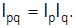
Эта связь обеспечивается, если один из индексов-сомножителей вычисляется по базисному весу, а второй – с текущим соизмерителем:
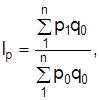
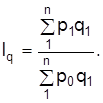
Или наоборот, один индекс – по текущему весу, а второй – с базисным соизмерителем:
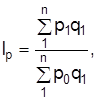
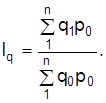
Взаимосвязаны также индексы прямых и обратных показателей. Например, индекс трудоемкости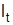 
и производительности труда 
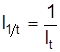или индекс потребительских цен 
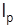и покупательной способности денежной единицы 
.
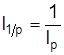Например, если потребительские цены на товары выросли на 7,5%, то покупательная способность денежной единицы снизилась на 7%:
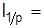1:1,075=0,930.
В рамках системы взаимозависимых индексов определяется роль каждого отдельного фактора в относительном или абсолютном изменении агрегата.
Абсолютное изменение определяется как разница между числителем и знаменателем соответствующего индекса. Например, абсолютное изменение товарооборота в целом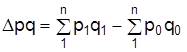 
раскладывается на две составляющие:
за счет изменения цен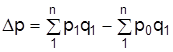 
и за счет изменения физического объема товаров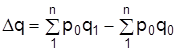 
.
Пример. Расчет сводных взаимозависимых индексов рассмотрим по данным рынка автобензина в регионе (табл. 8.1).
Таблица 8.1
| Марка бензина | Продано за период, тыс. л | Цена за 1 л в периоде, грн. | Товарооборот, тыс. грн. | ||||
базисный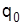 
| текущий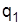 
| базисном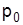 
| текущем 
| 
| 
| 
| |
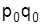
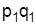
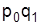
| А-76 | 0,46 | 0,48 | 45,6 | 43,7 | |||
| А-92 | 0,55 | 0,58 | 63,8 | 60,5 | |||
| А-95 | 0,60 | 0,66 | 82,5 | 75,0 | |||
| Всего | – | – | Х | Х | 191,9 | 179,2 |
Индекс товарооборота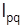 
=191,9/177,0=1,084 показывает, что стоимость проданного автобензина в целом по региону увеличилась на 8,4%.
Как свидетельствует индекс цен 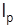=191,9/179,2=1,071, цены на бензин трех марок выросли в среднем на 7,1%.
Индекс физического объема составляет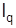 
=179,2/177,0=1,012, т.е. объем проданного автобензина увеличился в среднем на 1,2%.
Произведение взаимозависимых индексов 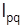=1,071*1,012=1,084 подтверждает результаты расчета.
Абсолютный прирост стоимости проданного автобензина в целом составляет: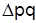 
=191,9-177,0=14,9 тыс. грн., в том числе за счет повышения цен 
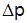=191,9 - 179,2=12, 7 тыс. грн., за счет увеличения объемов продажи – 
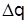=179,2-177,0=2,2 тыс. грн.
Сводные индексы могут определяться также как средние соответствующих индивидуальных индексов. Условиями применения средневзвешенных индексов являются однонаправленность изменений составляющих индивидуальных индексов и сравнимость элементов во времени или пространстве.
Средневзвешенный индекс – это среднее индивидуальных индексов, взвешенных на объемы, имеющие одинаковую размерность и зафиксированные на неизменном уровне.
Такими объемами являются известные уже агрегаты: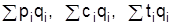 
Уровень, на котором фиксируются объемы, выбирается, исходя из агрегатной формулы соответствующего индекса.
Средневзвешенный индекс цен определяют по тождественному агрегатному индексу
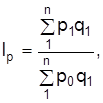
где условный товарооборот 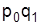вычисляется через индивидуальный индекс цен 
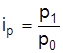, отсюд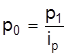а 
, а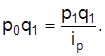 
Следовательно, средневзвешенный индекс цен и любого другого соизмерителя определяется по формуле средней гармонической взвешенной
