Основные понятия
Выборочный метод – это система научных принципов случайного отбора определенной части совокупности, которая представляла бы всю совокупность и характеристики которой служили бы надежной основой статистического вывода.
Совокупность, из которой отбираются элементы для обследования, называют генеральной, а совокупность, которую непосредственно обследуют, – выборочной. Статистические характеристики выборочной совокупности рассматриваются как оценки соответствующих характеристик генеральной совокупности. Поскольку выборочная совокупность не точно воспроизводит структуру генеральной, то выборочные оценки также не совпадают с характеристиками генеральной совокупности. Разногласия между ними называют погрешностями репрезентативности. По причинам возникновения эти погрешности делятся на систематические ( тенденциозные) и случайные. Систематические погрешности возникают при условии, что во время формирования выборочной совокупности нарушается принцип случайности отбора (предубежденный отбор элементов, несовершенная основа выборки и тому подобное). Случайные погрешности –- это следствие случайности отбора элементов совокупности для обследования.
При организации выборочного обследования важно предотвратить возникновение систематических погрешностей. Что касается случайных погрешностей, то избежать их невозможно, однако на основании теории выборочного метода можно определить их размер и по мере возможности регулировать.
В практике выборочных наблюдений используют два типа выборочных оценок – точечные и интервальные. Точечная оценка – это значение параметра по данным выборки: выборочная средняя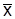 
или выборочная частица p. Интервальная оценка – это интервал значений параметра, рассчитанный по данным выборки для определенной вероятности, т.е. доверительный интервал. Его границы определяются на основе точечной оценки и граничной погрешности выборки 
:
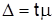для средней 
для частости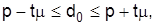 
где 
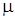– средняя, или стандартная погрешность выборки;
t – квантиль распределения вероятностей (доверительное число);
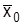и 
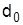– средняя и частость генеральной совокупности.
Стандартная погрешность выборки 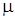является средним квадратичным отклонением выборочных оценок от значений параметра генеральной совокупности:
при повторном отборе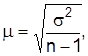 
при бесповторном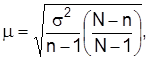 
где 
– выборочная дисперсия; n и N – соответственно объем выборочной и генеральной совокупностей.
При практическом использовании приведенных формул следует учитывать, что:
1) дисперсия частости является произведением частостей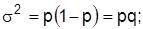 
,
2) в больших по объему совокупностях (30 и больше единиц) поправка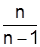 
не вносит существенных изменений в расчеты, а поэтому учитывается только в малочисленных (малых) выборках;
3) корректирующий множитель для бесповторной выборки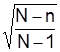 
при малых величинах 
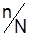приближается к 1, а поэтому при 1–5%-ной выборке расчет ведется по формуле для повторной выборки.
Предельная погрешность выборки 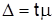– это максимально возможная погрешность для принятой вероятности F(х). Доверительное число tуказывает, как соотносятся предельная и стандартная погрешности. Так, t=1для вероятности 0,683; t=2для вероятности 0,954; t=3 для вероятности 0,997.
Следовательно, применяют такие формулы предельной погрешности выборки.
Повторная выборка Бесповторная выборка
Для средней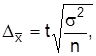 
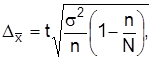
Для частости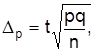 
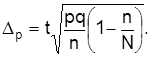
Как видно из формул, размер предельной погрешности зависит от вариации признака , объема выборки nи ее частости в генеральной совокупности 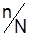, принятого уровня вероятности, которому отвечает квантиль t..
При малых выборках (
) квантиль tопределяют по распределению вероятностей Стьюдента. В приложении приведены значения t для F(х) = 0,95и числа степеней свободы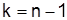 
.
Пример. По данным анализа плавки легированной стали (10 проб) содержание никеля в среднем 4,25% при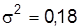 
. Предельная погрешность выборки с вероятностью F(х)=0,95 
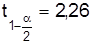составляет
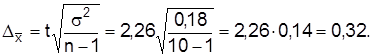
Доверительные границы: 4,25±0,32, т.е. с вероятностью 0,95 можно утверждать, что содержание никеля в легированной стали не меньше 3,93 и не больше 4,57%.
При сравнении точности выборочных оценок используют относительную погрешность выборки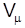 
, которая показывает, на сколько процентов выборочная оценка отклоняется от параметра генеральной совокупности:
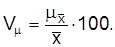
В нашем примере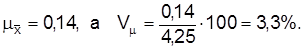 
Относительную погрешность выборки можно рассчитать на основании коэффициента вариации признака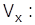 
для повторнойвыборки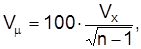 
для бесповторной выборки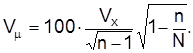 
Так, коэффициент вариации содержания никеля в легированной стали составляет
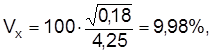
таким образом,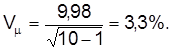 
Аналогично рассчитывают относительную погрешность выборки для частости:
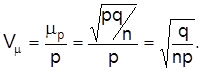
В практике выборочных обследований используют различные способы формирования выборочных совокупностей, в частности: простой случайный, механический, расслоения (районируемый), серийный.
Простой случайный отбор проводится жеребьевкой или на основании таблиц случайных чисел. Это классический способ формирования выборочной совокупности и именно на нем основывается теория выборочного метода.
При механическом отборе основой выборки является упорядоченная численность элементов генеральной совокупности. Отбор элементов осуществляется через одинаковые интервалы, шаг интервала зависит от частости выборки. Так, при 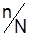=0,05 шаг интервала составляет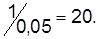 
Погрешность механической выборки вычисляется по формуле бесповторной выборки. Для моментных наблюдений, суть которых сводится к фиксации состояния непрерывного процесса на определенные моменты времени, используют формулу погрешности повторной выборки.
Расслаивания (районируемый) отбор предусматривает предварительную структуризацию генеральной совокупности и независимый отбор элементов в каждой составной части. Объем расслоенной выборки – это сумма частных выборок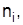 
, т.е. 
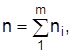, где m – число составных частей (групп, типовых районов и тому подобное).
При вычислении погрешности расслоения выборки используют среднюю групповых дисперсий
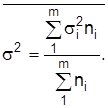
Как правило,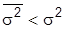 
, следовательно, погрешность расслоенной выборки меньшая, чем механической или простой случайной. Чаще всего используют отбор, пропорциональный численности составляющих совокупности, т.е. частость выборки для всех составляющих одинаковая.
При серийном отборе основа выборки состоит из серий элементов совокупности, связанных территориально (районы, поселки), организационно (фирмы, акционерные общества) и тому подобное. Серии отбираются по схеме механической или простой случайной выборки, обследованию подлежат все элементы серии. При вычислении погрешности выборки учитывается межсерийная вариация:
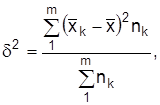
где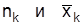 
– соответственно объем и средняя k-й серии.
Проектируя выборочные наблюдения, определяют минимально достаточный объем выборки, при котором выборочные оценки представляли бы основные свойства генеральной совокупности:
для повторного отбора для бесповторного
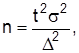
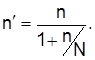
Для определения объема выборки nиспользуют оценки дисперсий аналогичных пробных обследований. Если такие обследования отсутствуют, можно воспользоваться соотношением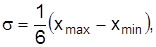 
адля частости взять наибольшее значение дисперсии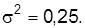 
Пример. Изучается отношение сельского населения региона к праву покупки–продажи земли.
Какой объем выборки будет гарантировать такую погрешность выборки для частицы, которая с вероятностью 0,954 (t=2) не превысит 5%? По результатам аналогичных обследований в других регионах 40% опрошенных поддерживают это право.
Опираясь на результаты аналогичных обследований, определим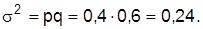 
Тогда минимально достаточный объем выборки будет составлять
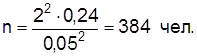
Если в основу расчета nположить относительную погрешность выборки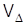 
, формулы соответственно модифицируются:
для средней для частости
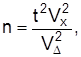
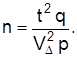
Статистическая гипотеза – это определенное предположение относительно свойств генеральной совокупности, которое можно проверить по данным выборочного наблюдения. Гипотеза, которую необходимо проверить, формулируется как отсутствие разногласий между параметром генеральной совокупности G и заданной величиной а (нулевая гипотеза). Содержание ее записывают так: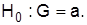 
Каждой нулевой гипотезе противопоставляют альтернативную На. В зависимости от весомости отклонений она формулируется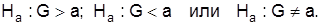 
Если выборочные данные противоречат гипотезе Н0, она отклоняется, если согласовываются – Н0не отклоняется. Проверка гипотез неминуемо связана с риском принятия ошибочного решения: риск I рода – отклонения верной нулевой гипотезы, риск II – принятие Н0, когда на самом деле верна альтернативная.
Правило, по которому гипотеза Н0отклоняется или не отклоняется, называют статистическим критерием. Математической основой любого критерия является статистическая характеристика Z,закон распределения которой известен, например, характеристика t-распределения Стьюдента.
Вероятность риска отклонения верной нулевой гипотезы называют уровнем существенности 
, а значение статистической характеристики для вероятности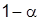 
– критическим значением 
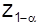. В приложении приведены критические значения наиболее распространенных статистических критериев. Если выборочное значение 
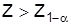, гипотеза Н0отклоняется, при 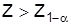не отклоняется.
В случае проверки справедливости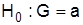 
против 
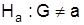используют двухсторонний критерий, критическое значение Zопределяется для 
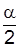, т.е. 
.
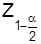Пример. На курсах восточных языков используют две методики обучения – новую и традиционную. Для сравнения эффективности новой методики проведено тестирование двух групп китайского языка по 100-балльной системе. Восемь слушателей, которые учились по новой методике, получили средний бал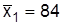 
при дисперсии 
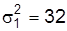; 10 слушателей, которые учились по традиционной методике, по такому же тесту имели средний бал 
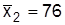при дисперсии 
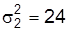. Разница между средними двух групп составляет 
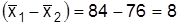баллов. Необходимо проверить, случайны ли эти разногласия, обусловлены ли они большей эффективностью новой методики. Нулевая гипотеза формулируется при предположении, что отклонение средних случайное, т.е. 
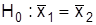. Альтернативная гипотеза предусматривает, что новая методика более эффективна, т.е. 
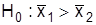. При такой формулировке 
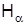проводится односторонняя проверка нулевой гипотезы. Статистической характеристикой проверки Н0естьнормируемое отклонение средних
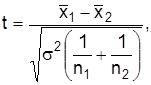
которое подчинено распределению вероятности Стьюдента с числом степеней свободы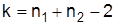 
.
В нашем примере k=8+10-2=16; оценка средней групповых дисперсий составляет:
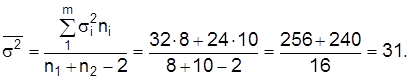
Тогда значение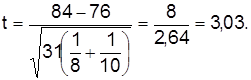 
Критическое значение одностороннего t-критерия при 
составляет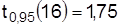 
, что меньше фактического (t=3,03). Следовательно, нулевая гипотеза 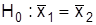отклоняется. С вероятностью 0,95 можно утверждать, что новая методика изучения восточных языков более эффективна.
