Предположим, что проводится испытание, заключающееся в бросании правильно выполненного игрального кубика два раза подряд. Возможные результаты такого испытания представим в виде таблицы:
| 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 |
| 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 |
| 5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 |
| 6,1 | 6,2 | 6,3 | 6,4 | 6,5 | 6,6 |
В каждой ячейке таблицы первая цифра – результат первого бросания, вторая цифра – результат второго бросания.
Как видно из таблицы, возможны 36 вариантов исхода двукратного бросания кубика. Попробуем рассчитать вероятность выпадения два раза подряд числа 6. Для правильно выполненного кубика все приведенные в таблице исходы равновероятны и, следовательно, выпадение двух шестерок, как и выпадение любой другой пары одинаковых чисел, имеет вероятность, равную 
. Но 
, то есть вероятность выпадения подряд двух шестерок равна произведению вероятности выпадения числа 6 на самое себя. Данный пример иллюстрирует теорему умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей.
Для случая двух независимых событий А и В:
Р(А и В)=Р(А)·Р(В).
Так как события А и В независимы, то каждому из m1 случаев, благоприятствующих событию А, соответствуют m2 случаев, благоприятствующих событию В. Таким образом, общее число случаев, благоприятствующих появлению событий А и В, равно, m1· m2 а общее число равновозможных событий равно n1·n2, где n1 и n2 – числа равновозможных событий соответственно для А и В. Отсюда вероятность совместного появления событий равна: 
.
Теорема умножения вероятностей усложняется, если определяется вероятность события, состоящего из совместного появления двух зависимых событий.
Вероятность наступления в некотором испытании одновременно двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое события имело место:
Р(А и В)=Р(А)·Р(B/A)=Р(В)·Р(A/B) – формула Байеса
При решении задач необходимо:
1. Выяснить, являются ли эти события независимыми или зависимыми;
2. Определить вероятности каждого отдельного события;
3. Определить вероятность одновременного наступления этих событий.
Задача:
В урне находится 10 белых и 20 черных шаров. Определить вероятность вынимания двух белых шаров подряд.
Дано: Решение:
m1 =10 Вероятность вынимания первого белого шара равна
m2=20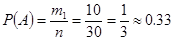 
n= m1+ m1 =30 Вероятность вынимания второго белого шара равна:
P(A и В)-? 
Тогда вероятность вынимания двух белых шаров подряд будет:
Р(А и В)=Р(А)·Р(B/A)=0,33·0,31≈0,1
Задача:
Считая, что рождение девочки или мальчика – это независимые и равновозможные события, определить вероятность появления в семье подряд трех девочек.
Дано: Решение:
P(D)=0,5 Согласно теореме умножения вероятностей для
P(D1 и D2 и D3)-? независимых событий:
Р(D1 и D2 и D3)=[Р(D)]3=0,53=0,125 (12,5%)
