25. 1. Мяч массой m = 300 г упал с высоты H = 1,23 м на асфальт и подскочил на ту же высоту. Продолжительность удара t = 0,10 с. Определить среднюю силу удара F. Как изменится эта сила, если мяч упадет на асфальтовую дорожку, наклоненную под углом a = 300 к горизонту? Какова была бы сила удара при падении не мяча, а куска пластелина той же массы?
Ответы: F =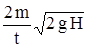 
+ m g = 32 Н.
В случае наклонной поверхности сила удара равна F cos a = 28 Н. Для пластилина в обоих случаях получается F =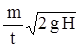 
+ m g = 18 Н.
25. 2. Конькобежец массой m1, стоя на льду, бросает кусок льда массой m2 со скоростью v2 под углом a к горизонту. Определить скорость конькобежца после броска.
Ответ: v1 = (m2 / m1) v2 cos a.
25. 3. С какой силой F давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v? Масса змеи – m, ее длина – l.
Ответ: F = m g (1 + v2 / (l g)).
25. 4.* Кусочек пластилина бросили вертикально вверх со скоростью v0. Одновременно такой же кусочек пластилина начал падать без начальной скорости с высоты H над исходным положением первого. При столкновении кусочки слиплись. Через какое время t, и с какой скоростью v слипшийся комок упадет до первоначального уровня бросания?
Ответы: t =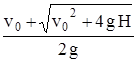 
; v = 
.
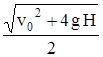25. 5. Какую работу A совершает человек при подъеме тела массой m = 2,0 кг на высоту h = 1,0 м с ускорением a =3,0 м/с?
Ответ: A = m (g + a) h» 26 Дж.
25. 6. Какую работу A нужно совершить, чтобы поднять на крышу здания свободно свисающий с нее конец веревки длиной l = 20 м и массой m = 3,0 кг?
Ответ: A = m g l / 2» 0,29 кДж.
25. 7. Какую работу A совершает двигатель автомобиля на первых S = 75 м пути, если это расстояние из состояния покоя автомобиль массой m =1,30 т проходит за t = 10 с, а коэффициент сопротивления движению равен m = 0,050?
Ответ: A = m (2 S / t2 + m g) S» 2,0·102 кДж.
25. 8. С вершины наклонной плоскости высотой h и длиной l соскальзывает брусок. Начальная скорость бруска – v0. Найти его скорость v в конце наклонной плоскости, считая трение пренебрежимо малым.
Ответ: v =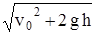 
.
25. 9. Автомобиль поднимается в гору со скоростью v = 60 км/ч. Спускаясь с той же горы, выключив двигатель, он движется равномерно с прежней скоростью. Какую мощность N развивает двигатель автомобиля при подъеме в гору? Масса автомобиля m = 2000 кг. Угол наклона горы a = 0,050.
Ответ: N = 2 m g v a» 33 кВт.
25. 10. От поезда массой M = 600 т, движущегося с постоянной скоростью по прямолинейному горизонтальному пути, отрывается последний вагон массой m = 60 тонн. Какое расстояние S пройдет этот вагон, если в момент его остановки поезд движется с постоянной скоростью v = 40 км/ч? Мощность локомотива, ведущего состав, постоянна и равна N = 1,0 МВт.
Ответ: S = 
» 3,0·102 м.
25. 11.* Ракета с работающим двигателем «зависла» над поверхностью земли. Какова мощность N, развиваемая двигателем, если масса ракеты равна m, а скорость истечения газов из двигателя – v? Изменением массы ракеты за время «зависания» можно пренебречь.
Ответ: N = m g v / 2.
25. 12. Шар массой m = 3 кг находится на высоте h = 3 м над столиком, укрепленным на пружине. Определить максимальное сжатие x пружины при падении шарика, если ее жесткость k = 700 н/м. Массами пружины и столика пренебречь.
Ответ: x = 
» 0,5 м.
25. 13.* Легкая вертикально расположенная пружина жесткостью k = 70 Н/м прикреплена одним концом к полу, а другим – к горизонтальной пластине. На пластину положили шар, после чего пружину сжали, а затем отпустили. На какую величину x была деформирована пружина, если после отрыва от пластины шар подлетел на высоту h = 50 см? Масса пластины с шаром равна m = 200 г.
Ответ: x = 
» 20 см.
25. 14.* Шарик массой m прикреплен двумя одинаковыми пружинами жесткости k к коробке массой M (рис. 59). Пружины расположены вертикально. Коробка падает с некоторой высоты на пол. В начальный момент времени пружины были не деформированы, а шарик и коробка неподвижны. С какой высоты h должна подать коробка, чтобы она подпрыгнула после абсолютно неупругого столкновения с полом? Размеры коробки достаточны для упругой деформации пружин.
Ответ: h ³ 
.
25. 15. Шар массой m = 1 кг катился по горизонтальному столу со скоростью v = 5 м/с. Ударившись о такой же покоившийся шар, он сообщил ему скорость v2 = 3 м/с, направленную под углом a = 530 к своей первоначальной скорости. С какой скоростью 
1 будет двигаться после столкновения первый шар?
Ответ: v1 = 4 м/с; угол между скоростями 1 и равен a1 = 370.
25. 16. На гладкой поверхности лежит брусок массой M. Летящая горизонтально со скоростью v0 пуля массой m пробивает его, расходуя на нагревание окружающей среды половину своей энергии. Какую скорость v пуля сообщает бруску?
Ответ: v =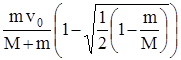 
.
25. 17.* Тело массы m = 1,0 кг разгоняется из состояния покоя переменной силой, причем произведение силы F на скорость v остается величиной постоянной, равной F v = P = 50 (Н м) / с.
а) Определите, за какое время t1 тело достигнет скорости v1 = 10 м / с.
б) Постройте график зависимости скорости от времени, v = v(t).
в) Определите с помощью этого графика путь S, пройденный телом за время t1.
Ответы:
а) t1 =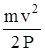 
» 1,0 с. б) график функции v = 10 
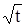, в) S» 6,7 м.
25. 18.* На вершине горки, имеющей вид полусферы радиуса R, лежит маленький кубик массой M. В него попадает горизонтально летящая пуля массой m и застревает. Какой минимальной скоростью v должна обладать пуля, чтобы заставить кубик сразу же оторваться от горки? Какая часть x кинетической энергии пули переходит при этом в тепло? На каком расстоянии S от основания горки упадет кубик?
Ответы: v =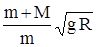 
; x = 
; S = R (
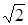– 1).
25. 19. Ареометр погрузили в воду и слегка толкнули в вертикальном направлении. Вычислить период T возникших в результате этого малых колебаний. Масса ареометра m = 50 г, радиус его цилиндрической части r =
5,0 мм. Сопротивлением воды пренебречь.
Ответ:. T =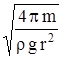 
» 3,6 с.
25. 20. Тяжелая тележка скатывается с ускорением a по наклонной плоскости, образующей угол a с горизонтом. Найти период колебаний математического маятника длины l, установленного на тележке.
Ответ:. T = 2 p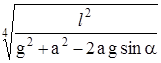 
.
25. 21*. Шарик массой m подвешен на нерастяжимой нити длиной l и привязан резинкой жесткостью k к стене (рис. 60). В положении равновесия резинка расположена горизонтально и не растянута. Найдите период малых колебаний шарика в плоскости рисунка. Массой нити и резинки пренебречь.
Ответ:. T = p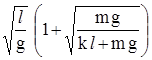 
.
25. 22*. На рисунке 61 представлен график зависимости проекции ускорения aX частицы, движущейся вдоль оси x, от ее координаты, отсчитываемой от начала движения из состояния покоя. Через какой промежуток времени t ускорение станет равным нулю? Какова будет скорость v к этому моменту времени?
Ответы:
t =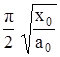 
» 0.31 с, v = 
» 0,4 с.
Здесь из графика взяты величины: a0 = 2 м/с и x 0 = 0,08 м.
25. 23. На абсолютно гладкую горизонтальную поверхность стола положили брусок массой M = 10 кг и прикрепили его к стене посредством горизонтально расположенной пружины. В брусок попадает и застревает в нем пуля массой m = 10 г, летевшая со скоростью v = 500 м/с вдоль оси пружины. В результате брусок с застрявшей в нем пулей стал совершать колебательные движения с амплитудой A = 10 см. Найти период колебаний T.
Ответ:. T = 2 p A (M + m) / (m v)» 1,3 с.
25. 24. К свободно подвешенной пружине с коэффициентом жесткости k =32 Н/м прицепили гирю массой 500 г и отпустили без начальной скорости. Как, начиная с этого момента, будет изменяться со временем удлинение пружины?
Ответ: x = x0 (1 – coswt), где x0 = m g / k» 15 см, w =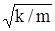 
» 8,0 с-1.
25. 25*. Два шара массами M и m, соединены невесомой пружиной жесткостью k и подвешены к потолку с помощью тонкой нити (рис. 62). Нить пережигают, и шары падает в однородном поле тяжести. Как с течением времени t изменяется деформация x пружины?
Ответ: x = x0 cos(w t), где x0 = 
, w =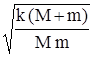 
.
25. 26. Доска, на которой лежит брусок, совершает гармонические колебания в горизонтальной плоскости. Амплитуда колебаний – A, коэффициент трения между доской и бруском равен m. При какой частоте колебаний n брусок не будет скользить по доске?
Ответ: n £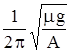 
.
 |
ОГЛАВЛЕНЕ
I ВВЕДЕНИЕ...................................................................................... 3
§ 1. Предисловие............................................................................................. 3
§ 2. Что необходимо знать и уметь, чтобы успешно решать задачи по физике 5
§ 3. Стратегия – залог успеха......................................................................... 6
II КИНЕМАТИКА............................................................................. 9
§ 4. «Генерал-законы» кинематики............................................................... 9
§ 5. Чего проще – ответ в одну строчку...................................................... 13
§ 6. Не так страшен черт, как его малюют.................................................. 18
§ 7. Разделяй и властвуй.............................................................................. 20
§ 8. Чудеса зазеркалья................................................................................. 22
§ 9. Умный в гору не пойдет, умный гору обойдет.................................... 24
§ 10. Перейдем в другую систему отсчета.................................................. 26
§ 11. График – не только картинка.............................................................. 33
§ 12. Хочешь научиться решать задачи по кинематике – решай их.......... 37
III ДИНАМИКА.............................................................................. 40
§ 13. «Генерал-законы» динамики.............................................................. 40
§ 14. «Запрягаем тройку» законов Ньютона.............................................. 43
§ 15. От грузов до космических тел............................................................ 47
§ 16. Не поскользнуться бы......................................................................... 52
§ 17. «Персональную тройку» – каждому.................................................. 59
§ 18. Задачи статики..................................................................................... 65
§ 19. Если хочешь научиться решать задачи динамики – решай их......... 67
IV ЗАКОНЫ СОХРАНЕНИЯ....................................................... 71
§ 20. «Генерал-законы» раздела................................................................. 71
§ 21. Изменение и сохранение импульса..................................................... 73
§ 22. Работа, мощность, энергия................................................................. 81
§ 23. Одного закона изменения может оказаться мало.............................. 91
§ 24. Механические колебания.................................................................... 98
§ 25. Задачи для самостоятельного решения............................................ 105
Селюк Борис Васильевич,
Елисеев Юрий Григорьевич
УЧИСЬ РЕШАТЬ ЗАДАЧИ
ПО ФИЗИКЕ
 |
Редактор Л.В. Бушуева
Подписано к печати 27.09.04. Формат 60×84 1/16
Бумага офсетная.Усл. п. л. 8,0. Уч.-изд. л. 8,0. Печать ризографическая.
.Тираж 100 экз. Заказ №
Отпечатано в типографии ЧП Паскалев.А.А.
Смоленск, ул. Верхне-Сенная, 4. Тел.: 38-19-14.
