19. 1. Гирю массой m, подвешенную на нити, поднимают вверх с постоянным ускорением из состояния покоя. Каково будет перемещение S гири за время t после начала движения, если жесткость нити k, а ее удлинение составляет D l?
Ответ: S = 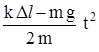 .
.
19. 2. Вагон движется по горизонтальному пути с постоянным ускорением a. К потолку вагона прикрепили отвес. Найти угол a отклонения отвеса от вертикали и силу T натяжения нити, если масса отвеса равна m.
Ответы: a = arctg (a /g); T = m  .
.
19. 3*. Автомобиль массой M поднимается вверх по дороге с постоянной скоростью. Дорога составляет с горизонтом угол a. Найти силу взаимодействия ведущих (задних) колес с поверхностью дороги. Расстояние между осями автомобиля – L, центр тяжести находится посредине между ними на расстоянии H от поверхности дороги. Силой сопротивления пренебречь.
Ответ: F = M g  .
.
19. 4. Искусственный спутник Земли, используемый в системе телевизионной и радиосвязи, запущен в плоскости земного экватора так, что все время находится над одной и той же точкой поверхности Земли. Во сколько раз радиус RC орбиты спутника больше радиуса Земли RЗ = 6400 км?
Ответ:  =
=  » 6,6, где g = 9,8 м/с2, а T = 24 ч.
» 6,6, где g = 9,8 м/с2, а T = 24 ч.
19. 5. Две звезды массами m1 и m2, расстояние между которыми равно l, вращаются около их общего центра масс по круговым орбитам. Найти период T обращения звезд.
Ответ: T = 2 p l  .
.
 19. 6. Воздушный шар, масса которого с баллоном M = 135 кг, а объем V = 156 м3, равномерно опускается. Какова масса m балласта, который нужно сбросить, чтобы шар начал равномерно подниматься с такой же скоростью? Плотность воздуха r = 0,8 кг/м3.
19. 6. Воздушный шар, масса которого с баллоном M = 135 кг, а объем V = 156 м3, равномерно опускается. Какова масса m балласта, который нужно сбросить, чтобы шар начал равномерно подниматься с такой же скоростью? Плотность воздуха r = 0,8 кг/м3.
Ответ: m = 2 (M – r V)» 20 кг.
 19. 7. Найти силу T натяжения нити и ускорение a грузов в системе, показанной на рисунке 35. Трением пренебречь.
19. 7. Найти силу T натяжения нити и ускорение a грузов в системе, показанной на рисунке 35. Трением пренебречь.
Ответы:
T =  (sin a + sin b);
(sin a + sin b);
a = g  .
.
19. 8*. Клин с углом a при основании может скользить по гладкой горизонтальной поверхности. При каком соотношении масс m1 и m2 грузов, связанных нитью, перекинутой через блок (рис. 36), клин будет неподвижен, и при каком он будет перемещаться влево или вправо? Коэффициент трения между грузом массой m2 и клином равен m.
Ответы:
Клин неподвижен при sin a – m cos a £  £ sin a + m cos a;
£ sin a + m cos a;
если  £ sin a – m cos a, то клин скользит влево;
£ sin a – m cos a, то клин скользит влево;
если  ³ sin a + m cos a, то – вправо.
³ sin a + m cos a, то – вправо.
19. 9*. Брусок массой m1 находится на доске массой m2, которая лежит на гладкой горизонтальной плоскости (рис. 37). Коэффициент трения  между бруском и доской равен m. К доске приложена горизонтально направленная сила
между бруском и доской равен m. К доске приложена горизонтально направленная сила  , зависящая от времени по закону F = a t, где a = const. Найти ускорения a1 и a2 движения бруска и доски. Построить графики зависимостей a1(t) и a2(t).
, зависящая от времени по закону F = a t, где a = const. Найти ускорения a1 и a2 движения бруска и доски. Построить графики зависимостей a1(t) и a2(t).
Ответы: Если t £ t0 = (m1 + m2) m g / a, то a1 = a2 = a t / (m1 + m2). При t > t0 величина a1 = m g, а ускорение a2 = (a t – m m1 g) / m2.
19. 10*. На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести автомобиля находится на высоте h = 1,0 м, ширина следа автомобиля l = 1,5 м. Определите скорость v, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит.
Ответ: v ³ 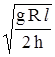 » 98 км/ч.
» 98 км/ч.
19. 11*. Коэффициент жесткости резинового жгута длины l и массы m равен k. Кольцо, изготовленное из этого жгута, вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через центр кольца. Время одного оборота – T. Определить радиус R вращающегося кольца.
Ответ: R =  .
.
19. 12. Однородная лестница прислонена к идеально гладкой стене. При каком предельном угле a наклона лестницы к полу она еще не проскальзывает, если коэффициент трения между полом и лестницей равен m?
Ответ: a =arcctg (2 m).
19. 13. На дне бассейна лежит тонкий стержень длиной L = 1,0 м, состоящий из двух половин плотностью r1 = 0,50 г/см3 и r2 = 2,5 г/см3. В бассейн наливают воду. Плотность воды r = 1,0 г/см3. При какой глубине h воды в бассейне стержень будет составлять с поверхностью воды угол a = 450?
Ответ: h =  » 71 cм.
» 71 cм.
19. 14*. На земле лежат вплотную два одинаковых бревна цилиндрической формы. Сверху кладут такое же бревно. При каком коэффициенте трения m между ними они не раскатятся?
Ответ: m ³ 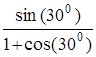 » 0,27.
» 0,27.
19. 15*. Однородный шар массы m и радиуса R подвешен на нити длиной l к гладкой вертикальной стене. Определить силу T натяжения нити и силу F давления шара на стену.
Ответы: T =  ; F =
; F =  .
.
19. 16*. Закрытая трубка длиной L, полностью заполненная жидкостью, составляет угол a с вертикальной осью, проходящей через ее нижний конец. В жидкости плавает легкая пробка. До какой угловой скорости w нужно раскрутить трубку вокруг оси, чтобы пробка погрузилась до середины трубки?
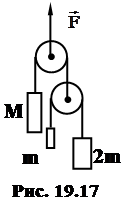 Ответ: w =
Ответ: w =  ;.
;.
19. 17. На рисунке 19.17 показана система, содержащая два подвижных блока и три груза, массы которых m, 2 m и M. Какую массу M нужно взять, чтобы сила натяжения верхней нити 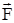 была равна 4 m g по модулю?
была равна 4 m g по модулю?
Ответ: M = 1,6 m.
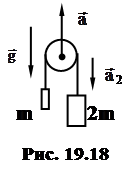 19. 18*. При каком ускорении блока
19. 18*. При каком ускорении блока  в системе, изображенной на рисунке 19.18, груз массой 2 m будет двигаться с ускорением, равным по модулю a2 = g / 10?
в системе, изображенной на рисунке 19.18, груз массой 2 m будет двигаться с ускорением, равным по модулю a2 = g / 10?
Ответы:  = – 7
= – 7  / 20, если
/ 20, если  2 =
2 =  / 10;
/ 10;
 = 13
= 13  / 20, если
/ 20, если  2 = –
2 = –  / 10.
/ 10.
19. 19*. По наклонной плоскости с углом наклона a движется вниз кубик массой m. Он скользит по плоскости двумя выступами, совпадающими с передним и задним (по направлению движения) нижними ребрами куба. Высота выступов пренебрежимо мала. Коэффициент трения выступов о наклонную плоскость равен m. Определите силы реакции F1 и F2 наклонной плоскости в процессе движения.
Ответы: F1 = m g cos a (1 + m)  ;
;
F2 = m g cos a (1 – m)  .
.
IV ЗАКОНЫ СОХРАНЕНИЯ
Генерал-законы» раздела
«В классической механике законы сохранения импульса и энергии являются следствиями законов Ньютона. Однако указанные понятия и соответствующие им законы сохранения в физике имеют более широкий смысл, и их область применимости выходит далеко за рамки классической механики.
«Импульсом частицы называют произведение ее массы на скорость: 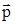 = m
= m  . Импульсом системы называют сумму импульсов частей системы:
. Импульсом системы называют сумму импульсов частей системы:
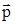 =
=  . (20.1)
. (20.1)
«Закон изменения импульса (ЗИИ): в инерциальной системе отсчета изменение импульса системы равно произведению суммы всех внешних сил на промежуток времени, в течение которого происходит это изменение:
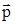 2 –
2 – 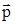 1 =
1 =  Dt. (20.2)
Dt. (20.2)
Из ЗИИ (20.2) следует, что при определенных условиях ( t = 0) импульс системы может сохраняться.
t = 0) импульс системы может сохраняться.
«Закон сохранения импульса: если система замкнута (нет внешних воздействий), то ее импульс остается неизменным. На практике редко приходится иметь дело с замкнутыми системами, поэтому при решении задач классической механики лучше, чтобы избежать ошибок, применять закон изменения импульса (20.2).
«Импульс системы равен произведению ее массы m на скорость движения центра масс  Ц:
Ц:
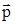 = m
= m  Ц. (20.3)
Ц. (20.3)
Поэтому при сохранении импульса системы сохраняется и скорость движения центра масс.
«Работа постоянной силы  на перемещении
на перемещении  есть физическая величина, определяемая равенством:
есть физическая величина, определяемая равенством:
A = 
 = F S cos a, (20.4)
= F S cos a, (20.4)
где a – угол между векторами  и
и  .
.
Если сила не остается постоянной, то работа равна сумме элементарных работ DAi, то есть работ на достаточно малых перемещениях D  i, для которых можно пренебречь изменением силы:
i, для которых можно пренебречь изменением силы:
DAi = Fi DSi cos ai, (20.5)
A =  =
= 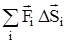 =
=  . (20.6)
. (20.6)
Здесь i – номер участка траектории, ai – угол между силой  i и перемещением D
i и перемещением D  i на этом участке.
i на этом участке.
Часто всю траекторию движения приходится разбивать на бесконечно большое число бесконечно малых участков. В этих случаях суммирование в (20.6) заменяется интегрированием.
«Сумму работ всех внешних сил, приложенных к системе, называют работой над системой A. Работа самой системы
A¢ = – A. (20.7)
«Мощностью N механизма, совершающего элементарную работу DA за малый промежуток времени Dt, называют отношение
N = DA / Dt. (20.8)
«Если механизм обеспечивает существование силы  , точка приложения которой движется со скоростью
, точка приложения которой движется со скоростью  , то его мощность вычисляется по формуле
, то его мощность вычисляется по формуле
N = F v cos a, (20.9)
где a – угол между направлениями  и
и  .
.
«Кинетической энергией частицы массой m, которая движется со скоростью v, называют величину
EК = m v2 / 2. (20.10)
Кинетическая энергия системы равна, по определению, сумме кинетических энергий частей системы.
«Потенциальной (консервативной) называют силу, работа которой не зависит от того, по какой траектории движется точка приложения. Работа потенциальной силы AП равна разности значений некоторой функции EП, называемой потенциальной, в начальном и конечном положениях:
AП = EП1 – EП2. (20.11)
Потенциальными являются, например, силы тяжести и упругости. Соответствующие потенциальные функции имеют вид: EП = m g h и EП = k x2 / 2.
«Потенциальной энергией EП системы называют физическую величину, равную работе внутреннихпотенциальных сил при переходе системы их данного состояния в нулевое. Нулевое состояние – такое состояние, в котором потенциальная энергия полагается равной нулю. Выбор нулевого состояния произволен.
«Потенциальная энергия системы «груз – Земля» равна
EП = m g h (20.12)
при условии, что высота подъема h груза массой m много меньше радиуса Земли, и что в качестве нулевого состояния принято состояние системы, для которого h = 0.
«Потенциальная энергия пружины жесткостью k, деформированной на величину x, равна
EП = k x2 / 2, (20.13)
если за нулевое принято состояние недеформированной пружины.
«Помимо потенциальной энергии системы (внутренней потенциальной энергии) иногда рассматривают потенциальную энергию во внешнем поле (внешнюю потенциальную энергию), равную работе внешних потенциальных сил при переходе в нулевое состояние. Чтобы избежать недоразумений, будем употреблять термин «потенциальная энергия» в смысле внутренней потенциальной энергии системы.
«Механической энергией системы называют сумму ее кинетической и потенциальной энергий:
E = EК + EП. (20.14)
«Закон изменения механической энергии заключается в следующем: изменение механической энергии системы равно сумме работ внутренних непотенциальных (AН) и внешних (A) сил. Закон выражается формулой:
E2 –E1 = AН + A. (20.15)
«Физическую величину U, изменение которой DU в изолированной системе равно взятой с обратным знаком работе внутренних непотенциальных сил, называют внутренней энергией:
DU = – AН. (20.16)
Над изолированной системой, по определению, не совершается работа и эта система не получает тепло.






