 Совокупность n дифференциальных уравнений вида
Совокупность n дифференциальных уравнений вида
х'1 + а11х1 + а12х2 + … + а1nхn = f1(t),
x'2 + а21x1 + а22x2 + … + а2nxn = f2(t),
— — — — — — — — — — — —
x'n + аn1x1 + аn2x2 + … + аnnxn = fn(t).
где t – аргумент, x1, x2, …, xn – неизвестные функции, называется системой линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.
Проинтегрировать эту систему, значит найти ее решение, т.е. систему функций x1(t), x2(t), …, xn(t), обращающих равенства в тождества.
Пример выполнения задания 3
Решим систему 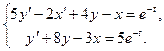
Решение.
Данную систему решим методом исключения.
Исключаем х из данных уравнений. Из второго уравнения имеем:
х =  (у' + 8 у – 5 е-t).
(у' + 8 у – 5 е-t).
Продифференцируем его по аргументу t:
х' =  (у'' + 8 у' + 5 е-t), и подставим в первое уравнение. После упрощения получим:
(у'' + 8 у' + 5 е-t), и подставим в первое уравнение. После упрощения получим:
у'' + у' – 2 у = -4 е-t (*).
Это линейное дифференциальное уравнение. Найдем его общее решение у = у0 + ỹ.
Корни характеристического уравнения k 2 + k – 2 = 0
k 1 = 1, k 2 = -2.
Общее решение однородного уравнения у0 = С1еt + C2e-2t.
Частное решение неоднородного уравнения (*) ищем в виде
 = Аe -t.
= Аe -t.
Найдем  = - Ае -t,
= - Ае -t,  = Ае -t и подставим в уравнение (*). Получим А = 2, следовательно,
= Ае -t и подставим в уравнение (*). Получим А = 2, следовательно,  =2 e -t.
=2 e -t.
у = С1et + C2e-2t + 2e-t. Определим х, пользуясь равенством
х =  (у' + 8у – 5е-t). Найдем у' = C1et – 2C2e-2t – 2e-t.
(у' + 8у – 5е-t). Найдем у' = C1et – 2C2e-2t – 2e-t.
После подстановки у и у':
х =  (C1et – 2C2e-2t – 2e-t + 8(C1et + C2e-2t + 2e-t) – 5e-t).
(C1et – 2C2e-2t – 2e-t + 8(C1et + C2e-2t + 2e-t) – 5e-t).
Упростив, получим х = 3С1et + 2e-2t + 3e-t.
 Общим решением данной системы будут функции:
Общим решением данной системы будут функции:
х = 3С1et + 2e-2t + 3e-t,
у = С1еt + C2e-2t + 2e-t.
Модуль 8
Ряды
Задачи для решения
Задание 1
Исследовать на сходимость числовые ряды.
Варианты
- а)
 ; б)
; б) 
в)  ; г)
; г)  .
.
2. а)  ; б)
; б) 
в) 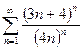 ; г)
; г)  .
.
3. а)  ; б)
; б) 
в)  г)
г)  .
.
4. а)  б)
б) 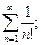
в)  г)
г)  .
.
5. а)  б)
б) 
в)  г)
г)  .
.
6. а)  б)
б) 
в)  г)
г) 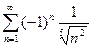 .
.
7. а)  б)
б) 
в)  ; г)
; г)  .
.
8. а)  б)
б) 
в)  г)
г)  .
.
9. а)  б)
б) 
в)  г)
г)  .
.
10. а)  б)
б) 
в)  г)
г)  .
.
Задание 2
Определить радиус и область сходимости степенных рядов.
Варианты
1. а)  ; б)
; б)  .
.
2. а)  ; б)
; б)  .
.
3. а)  ; б)
; б)  .
.
4. а)  ; б)
; б)  .
.
5. а)  ; б)
; б)  .
.
6. а)  ; б)
; б)  .
.
7. а)  ; б)
; б)  .
.
8. а)  ; б)
; б)  .
.
9. а)  ; б)
; б)  .
.
10. а)  ; б)
; б)  .
.
Задание 3
Разложить заданную функцию в ряд Фурье в интервале [-π; π].
Варианты
1. a) 
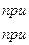


б) f(x) = 2x на отрезке [0;2] по косинусам.
2. a) 
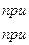


б) f(x) = 1 – x на отрезке [0;1] по синусам.
3. a) 
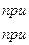


б)  на отрезке [0;4] по косинусам.
на отрезке [0;4] по косинусам.
4. a) 
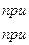


б) f(x) = x – 1 на отрезке [0;1] по косинусам.
5. a) 
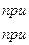


б) f(x) = 2 – 2 x на отрезке [0;1] по синусам.
6. а) 
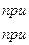


б)  на отрезке [-5;0] по косинусам.
на отрезке [-5;0] по косинусам.
7. а) 
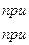


б) f(x) = 3 – x, на отрезке [0;3] по синусам.
8. а) 
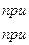


б) f(x) = 1 – 2 x на отрезке [0;1/2] по косинусам.
9. а) 
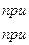


б) f(x) = -2 x на отрезке [0;1/2] по синусам.
10. а) 
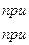


б)  на отрезке [0;4] по косинусам.
на отрезке [0;4] по косинусам.
Решение типовых задач
Задание 1
Исследовать на сходимость числовые ряды.
а)  ;
;
б) 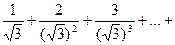
 +…;
+…;
в)  .
.
Задание 2
Определить радиус и область сходимости степенного ряда  .
.
Задание 3
Разложить функцию 
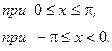 в ряд Фурье в интервале [-π; π].
в ряд Фурье в интервале [-π; π].
Решение типовых задач
Сведения из теории
Числовые ряды
Числовым рядом называют сумму бесконечной числовой последовательности вида
 =
=  .
.
Числа  называют членами ряда, un – общим членом ряда.
называют членами ряда, un – общим членом ряда.
Конечная сумма Sn =  называется n -ойчастичной суммой ряда.
называется n -ойчастичной суммой ряда.
Если существует конечный предел 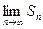 , ряд называется сходящимся, в противном случае – расходящимся.
, ряд называется сходящимся, в противном случае – расходящимся.






