Первым замечательным пределом называют предел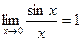 
.
Его используют для раскрытия неопределённостей вида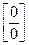 
.
Вторым замечательным пределом называют предел
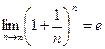или 
.
Его используют для раскрытия неопределённостей вида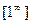 
.
Пример выполнения задания 1
а)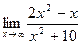 
.
В данном случае имеем неопределенность [ 
]. Для раскрытия неопределенности разделим числитель и знаменатель на наибольшую степень переменной, то есть, разделим на x 2.
.
б)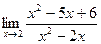 
.
При x →2 числитель и знаменатель дроби равны нулю. Неопределенность вида [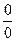 
]. Следовательно, необходимо данное выражение преобразовать.
Числитель и знаменатель данной дроби при x = 2 обращается в ноль, поэтому многочлены x 2- 5 x + 6 и x 2 - 2 x делятся без остатка на бином (x – 2) (теорема Безу).
в)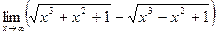 
.
В данном случае имеем неопределенность вида [∞-∞].
Умножаем выражение, стоящее под знаком предела, на такой множитель, чтобы получить разность квадратов: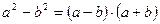 
. Чтобы не нарушать тождество, на сопряжённый множитель так же и разделим.
В результате получим:
.
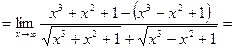
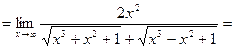
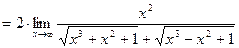
При x → + ∞ числитель и знаменатель дроби – бесконечно большие величины, имеем неопределенность вида [ ].
Для раскрытия неопределенности разделим числитель и знаменатель на x 2:
= 
.
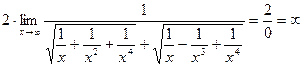г)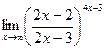 
.
Предел основания равен 1, а показатель степени стремится к бесконечности. Имеем неопределенность вида [1∞].
Для вычисления предела преобразуем выражение так, чтобы выделить второй замечательный предел.
.
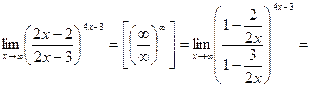
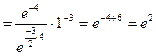д) 
.
В данном случае имеем неопределенность вида [ ].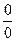
Для вычисления предела преобразуем выражение так, чтобы выделить первый замечательный предел.
=
.
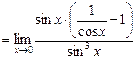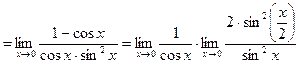Домножаем числитель и знаменатель дроби на х 2:
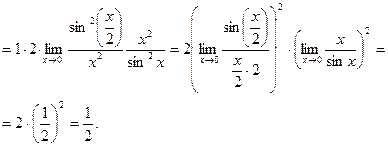
Сведения из теории
Непрерывность функции
Функция y = f(x) называется непрерывной в точке х = а, если
1) функция определена в этой точке и ее окрестности;
2) существует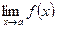 
;
3) предел фнкии равен значению функции в точке а, т.е.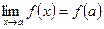 
.
Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке а, а сама точка а называется точкой разрыва.
Если 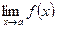не существует, но существует оба односторонних предела в точке а, которые не равны друг другу, то разрыв в точке а называется разрывом первого рода или скачком.
Если хотя бы один из односторонних пределов не существуют или равен бесконечности, а, следовательно, не существует и 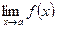, то разрыв в точке а называется разрывом второго рода.
Если 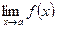существует, но функция f (x) в точке а не определена или определена, но так, что 
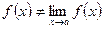, то разрыв в точке а называется устранимым.
Рассмотрим функцию:
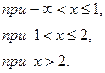
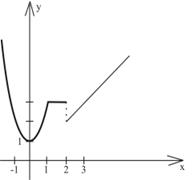Область определения ее – вся числовая ось. Разрывы возможны лишь в точках x = 1, x = 2, в которых функция изменяет аналитическое выражение. Найдем односторонние пределы в точках х = 1, х = 2.
При х = 1
; 
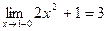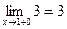так как f (1-0) = f (1+0) = 3, то в точке х = 1 функция непрерывна.
При х = 2
; 
,
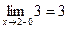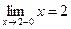так как f (2-0) ≠ f (2+0), то в точке
х = 2 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1.
Асимптоты графика функции
Под асимптотой графика функции понимают такую прямую линию, к которой неограниченно приближаются точки графика функции у = f (x) по мере их удаления в ± ∞.
Если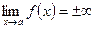 
, то х = а – уравнение вертикальной асимптоты.
Если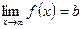 
, то у = b – уравнение горизонтальной асимптоты.
Если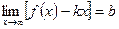 
, то у = kx + b – уравнение наклонной асимптоты.
