1. Найти область определения функции.
2. Выяснить четность, нечетность, периодичность.
3. Исследовать функцию на непрерывность, найти точки
разрыва и выяснить характер разрывов.
4. Найти асимптоты графика функции.
5. Найти нули функции (у = 0) и интервалы знакопостоянства
(у > 0, y < 0).
6. Найти критические точки (у' = 0) и интервалы монотонности
(у' > 0, y' < 0).
7. Найти экстремумы функции.
8. Найти критические точки, в которых у'' = 0, и интервалы выпуклости и вогнутости.
9. Найти точки перегиба.
10. Выполнить схематический чертёж.
Пример выполнения задания 4
Исследуем функцию:  и построим её график.
и построим её график.
Решение.
Найдем первую и вторую производные этой функции.
 .
.
 .
.
1. Область определения:
 .
.
2. Функция общего вида, непериодическая.
3. Точка разрыва функции х = 0.
 , в точке х = 0 разрыв второго рода.
, в точке х = 0 разрыв второго рода.
4.  , х = 0 – вертикальная асимптота.
, х = 0 – вертикальная асимптота.
 – горизонтальной асимптоты нет.
– горизонтальной асимптоты нет.
 , k = 1,
, k = 1,
 , b = 0,
, b = 0,
у = х – наклонная асимптота.
5. у = 0.
 ,
,  .
.
y > 0, при  ; y < 0, при
; y < 0, при 
6.  .
.
 ,
,  , x = 2,
, x = 2,


 |
7. y min(2) = 3.
при x  (-∞; 0) функция возрастает;
(-∞; 0) функция возрастает;
при x  (0; 2) функция убывает;
(0; 2) функция убывает;
при x  (2; +∞) функция возрастает.
(2; +∞) функция возрастает.
8. у'' = 0;  ≠ 0 – точек перегиба нет. При х = 0 вторая
≠ 0 – точек перегиба нет. При х = 0 вторая
производная не существует.
 9.
9.
График функции при  является
является
вогнутым.
10. График функции имеет вид, указанный на рисунке.
Пример выполнения задания 5
Выполним над комплексными числами указанные действия:
а)  ;
;
Воспользуемся формулой:
 ,
,
где k = 0,1,…, n -1.
Запишем комплексное число, заданное в алгебраической форме, в тригонометрической форме:  , где
, где
 ,
, 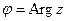 ,
,
 ,
,  .
.
Для данного числа 
 ;
;  ;
;  .
.
Следовательно,

 .
.

 , k = 0, 1, 2.
, k = 0, 1, 2.

б)  .
.
Воспользуемся формулой:
 .
.
Запишем данное комплексное число в тригонометрической форме.
 ,
,
 ;
;  ;
;  .
.
Следовательно,
 .
.
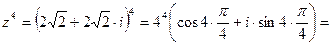
 .
.
II семестр
Вопросы
- Определение функции многих переменных, области, линии и поверхности уровня.
- Частные приращения и частные производные.
- Полное приращение и полный дифференциал.
- Производная сложной функции.
- Повторное дифференцирование.
- Дифференциал второго порядка.
- Экстремум функции двух переменных.
- Неопределенный интеграл и его свойства.
- Непосредственное интегрирование.
- Интегрирование по частям.
- Интегрирование путём внесения функции под знак дифференциала.
- Интегрирование рациональных функций.
- Интегрирование тригонометрических функций.
- Интегрирование иррациональных функций.
- Определенный интеграл и его геометрический смысл.
- Формула Ньютона-Лейбница.
- Методы интегрирования в определенном интеграле (подстановка, интегрирование по частям).
- Несобственные интегралы.
- Вычисление площадей плоских фигур в полярных и прямоугольных координатах.
- Вычисление длины дуги плоской кривой, вычисление объема тела вращения, площади поверхности вращения.
- Двойной интеграл в декартовых и полярных координатах.
- Вычисление двойного интеграла.
- Применение двойного интеграла.
- Тройной интеграл в декартовых, цилиндрических и сферических координатах.
- Применение тройного интеграла.
Модуль 4
Дифференциальное исчисление функций нескольких переменных
Задачи для решения
Задание 1
Найти частные производные функции z (х; у), заданной уравнением.
Варианты
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7. 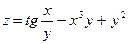 ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  .
.
Задание 2
Найти дифференциал второго порядка заданной функции.
Варианты
1. z = sin(2x + y) + 4; 2. z = cos(3 x + 2 y) – 5;
3. z = xy 2 – x 2 y; 4. z = cos(x – 2 y) + 16;
5. z = sin(x– 3y) – 3; 6. z = x 3 y 2 + x 2 y 3;
7. z = 2x3 y 2 – 3 x 2 y 3; 8. z = sin(3 x + 4 y) – 13;
9. z = 3 x 2 y – 2 y 2 x; 10. z = cos(5 x – y) + 6.
Задание 3
Найти производные сложных функций.
Варианты
1. a)  , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
2. а)  , если
, если 
 .
.
б)  , если
, если  ,
,  .
.
3. a)  , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
4. a)  , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
5. a)  , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
6. a)  , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
7. a) 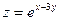 , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
8. a)  , если
, если 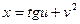 ,
,  .
.
б)  , если
, если  ,
,  .
.
9. a)  , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
10. a) 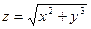 , если
, если  ,
,  .
.
б)  , если
, если  ,
,  .
.
Решение типовых задач
Задание 1
Найти частные производные функции z (х; у), заданной уравнением
z = х 2 y + у 2 х + cos(2 x – 3 y).
Задание 2
Найти дифференциал второго порядка для функции
z = sin (3 x - y) + e 2 x + y .
Задание 3
Выполнить дифференцирование сложных функций:
а)Найти производные  и
и  функции
функции  , если
, если 
б)Найти производную  функции
функции  , если
, если 
Пример выполнения задания 1
Найдём частные производные функции, заданной уравнением
z = х 2 y + у 2 х + cos(2 x – 3 y).
Решение.
Дифференцируем функцию двух переменных z = z(x; y) по х.
Другая переменная у при этом считается постоянной величиной.
 .
.
Дифференцируем функцию z по у, переменная х при этом считается постоянной величиной.
 .
.
Ответ: 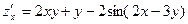 ,
,
 .
.
Пример выполнения задания 2
Найдём дифференциал второго порядка для функции
z = sin (3 x - y) + e 2 x + y .
Решение.
Определяем первые и вторые частные производные 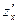 ,
,  ,
,  ,
,  ,
,  и подставляем их в формулу дифференциала второго порядка:
и подставляем их в формулу дифференциала второго порядка:

 ;
;
 ;
;
 ;
;
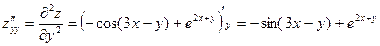 ;
;

Дифференциал второго порядка равен:

Ответ:

Пример выполнения задания 3
Выполним дифференцирование сложных функций.
а)Найдём производные  и
и  функции
функции  ,
,
если 
Решение.
Частные производные  и
и  сложной функции
сложной функции 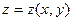 ,
,
если  , находят по формулам:
, находят по формулам:
 ,
,  .
.
Найдём частные производные  и
и  сложной функции
сложной функции  ,
, 






Подставим в формулы для нахождения  и
и 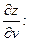



 .
.
Ответ:  ;
;  .
.
б)Найдём производную  функции
функции  , если
, если

Решение.
Пусть функция  - дифференцируемая функция аргументов x и y, а x и y являются дифференцируемыми функциями аргумента t. Сложная функция
- дифференцируемая функция аргументов x и y, а x и y являются дифференцируемыми функциями аргумента t. Сложная функция  также дифференцируема, и ее производная находится по формуле:
также дифференцируема, и ее производная находится по формуле:
 .
.
Найдём производную  функции
функции  .
.
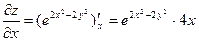 ,
,  ,
,
 ,
, 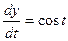 .
.
Полученные производные подставим в формулу для нахождения  .
.

 .
.
Модуль 5
Интегральное исчисление функции одной переменной
Задачи для решения
Задание 1
Непосредственным интегрированием найти следующие интегралы:
Вариант № 1 Вариант № 2
1. 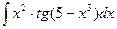 ; 1.
; 1.  ;
;
2. 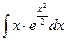 ; 2.
; 2. 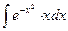 ;
;
3.  ; 3.
; 3. 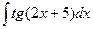 ;
;
4.  . 4.
. 4.  .
.
Вариант № 3 Вариант № 4
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2.  ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Вариант № 5 Вариант № 6
1. 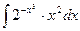 ; 1.
; 1.  ;
;
2.  ; 2.
; 2. 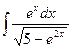 ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Вариант № 7 Вариант № 8
1.  ; 1.
; 1. 
2.  ; 2.
; 2. 
3.  ; 3.
; 3. 
4.  . 4.
. 4.  .
.
Вариант № 9 Вариант № 10
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2.  ;
;
3.  ; 3.
; 3.  ;
;
4.  ; 4.
; 4.  .
.
Задание 2
Проинтегрировать, выбрав нужный метод интегрирования.
Вариант № 1 Вариант № 2
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2. 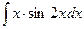 ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Вариант № 3 Вариант № 4
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2.  ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Вариант № 5 Вариант № 6
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2. 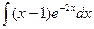 ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Вариант № 7 Вариант № 8
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2.  ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4. 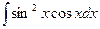 .
.
Вариант № 9 Вариант № 10
1.  ; 1.
; 1.  ;
;
2.  ; 2.
; 2. 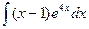 ;
;
3.  ; 3.
; 3.  ;
;
4.  . 4.
. 4.  .
.
Задание 3
Вычислить определённый интеграл.
Варианты
1.  ; 2.
; 2.  ; 3.
; 3.  4.
4. 
5.  6.
6.  7.
7.  8.
8.  9.
9. 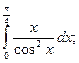 10.
10. 
Задание 4
Вычислить площадь фигуры, ограниченной данными линиями.
Варианты.
1. ху = 6, х + у = 7; 6. у = 2 х – х 2, у = 0;
2. у = 3 х – х 2, у = 0; 7. у = 6 х – х 2, у = 0;
3. ху = 8, х + у = 6; 8. у = 1 – х 2, у = 0, х < 0;
4. у = 4 х – х 2, у = 0; 9. у = 9 – х 2, х >0, у = 0;
5. у = 4 – х 2, у = 0, х > 0; 10. у = 25 – х 2, у = 0, х <0.
Задание 5
По формулам трапеций и парабол (Симпсона) приближенно вычислить интеграл.
Варианты
1.  ,
,  ; 6.
; 6. 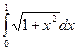 ,
,  ;
;
2.  ,
,  ; 7.
; 7.  ,
,  ;
;
3.  ,
,  ; 8.
; 8.  ,
,  ;
;
4.  ,
,  ; 9.
; 9. 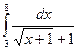 ,
,  ;
;
5.,; 10.,.
Решение типовых задач
Задание 1
Непосредственным интегрированием найти следующие интегралы:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 2
Проинтегрировать, выбрав нужный метод интегрирования.
а)  ;
;
б)  ;
;
в)  ;
;
Г).
Задание 3






