Як відомо, деяке ціле число а може бути чи не бути кратним натуральному числу b. Якщо а кратне b, то 
. Якщо а не кратне b, то це означає, що при діленні а на b з’являється відмінна від нуля і менша від дільника остача, тобто 
, де 
.
Наприклад.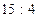 
. Маємо 
(остача 3), або 
.
Означення. Говорять, що ціле невід’ємне число а ділиться на натуральне число b з остачею, якщо існують такі цілі невід’ємні числа 
і 
, що , де .
Існування та єдиність неповної частки () і () встановлюється такою теоремою.
Теорема. Для будь-яких цілого і невід’ємного числа а і натурального числа b існує і причому єдина пара цілих невід’ємних чисел і , що , де 
.
Доведення.
1. Якщо а кратне b, то , а 
.
2. Якщо 
, то 
, де 
, бо 
.
3. Якщо 
і а не кратне b. Тоді серед чисел, кратних b, знайдуться два послідовні числа такі, що 
, або 
. Віднявши від усіх трьох частин подвійної нерівності добуток 
, дістанемо: 
. Позначимо 
. Тоді , де .
Доведемо, що пара чисел і єдина для даних чисел а і b. Справді, існує ще пара чисел 
, 
таких, що 
, де 
. Тоді за транзитивною властивістю рівності маємо 
. Нехай для визначеності 
. Тоді 
. З того, що 
і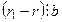 
випливає 
. Отже, 
і тому 
, де 
. Тому 
, звідки 
.
Теорему доведено.
Теорему про ділення з остачею застосовують в арифметиці і в багатьох інших розділах математики. На ній ґрунтується подання натуральних чисел системними числами, перехід від однієї позиційної системи числення до іншої, алгоритм Евкліда, а також техніка ділення натуральних чисел «кутом».
Ділення з остачею розглядається ще в початкових класах. Наприклад, 
(1 остача). Тоді 
.
Підкреслюється, що обов’язково остача повинна бути меншою від дільника.
Важливість ділення з остачею в тому, що воно лежить в основі алгоритму ділення багатоцифрових чисел.
Тема. Прості задачі на множення та ділення
І. Задачі на розкриття конкретного змісту арифметичної дії:
· множення – знаходження добутку як суми однакових доданків:
В трьох однакових коробках лежало по 6 олівців. Скільки всього лежало олівців?
по 6 ол. – 3 к.
? ол.
6 + 6 + 6 = 6 · 3 = 18 (ол.)
 |
· ділення – знаходження частки:
1) ділення на рівні частини:
Вчителька поділила 8 зошитів порівну між 4 учнями. Скільки зошитів одержав кожний учень?
по? з. – 4 уч.
8 з.
8: 4 = 2 (з.)
2) ділення на вміщення:
Маша розклала 8 кружечків в рядочки по 2 круга в кожному. Скільки рядочків отримала дівчинка?
по 2 кр. –? р.
8 кр.
8: 2 = 4 (р.)
ІІ. Задачі на збільшення, зменшення числа в кілька разів у прямій та непрямій формі:
· збільшення у прямій формі:
В перший корзині лежить 4 яблука, а в другій – в 3 рази більше. Скільки яблук лежить в другій корзині?
І. – 4 ябл.
ІІ. –? ябл., в 3 рази б.
4 · 3 = 12 (ябл.)
· збільшення в непрямій формі:
В Оленки було 5 іграшок, а це в 2 рази менше, ніж у Миколи. Скільки іграшок у Миколи?
Ол. – 5 ігр., в 2 р. м. або Ол. – 5 ігр.
М. –? ігр. М. -?, в 2 рази б.
5 · 2 = 10 (ігр.)
· зменшення в прямій формі:
На клумбі виросло 9 білих троянд, а червоних – в 3 рази менше. Скільки червоних троянд виросло на клумбі?
Б. – 9 тр.
Ч. –? тр., в 3 р. м.
9: 3 = 3 (тр.)
· зменшення в непрямій формі:
В перший рядок поклали 8 квадратиків. Їх в 2 рази більше, ніж трикутників в другому ряду. Скільки поклали трикутників в другому ряду?
К. – 8 шт., в 2 р. б. або К. – 8 шт.
Т. –? шт. Т. –? шт., в 2 р. м.
8: 2 = 4 (тр.)
ІІІ. Задачі на кратне порівняння (з питаннями «У скільки разів більше...?», «У скільки разів менше...?»)
1) У Мишка було 18 іграшкових автомобілів та 3 іграшкових літака. У скільки разів більше у хлопчика автомобілів, ніж літаків?
Авт. – 18 шт.
у? р. б.
Л. – 3 шт.
18: 3 = 6 (р.)
2) Бабусі 54 роки, а її онучці 9 років. У скільки разів онучка молодша від бабусі?
Б. – 54 р.
у? р. м.
В. – 9 р.
54: 9 = 6 (р.)
ІV. Задачі на знаходження числа за однією його частиною та знаходження частини числа:
1) знаходження числа за однією його частиною:
У Маринки половина стрічки має довжину 9 см. Яка довжина всієї стрічки?
9 · 2 = 18 (см)
2) знаходження частини числа:
Було 24 горіхи. Третю частину їх витратили. Скільки горіхів витратили?
24: 3 = 8 (г.)
V. Задачі на знаходження невідомого компонента арифметичної дії:
1) знаходження невідомого множника:
Невідоме число збільшили у 3 рази і дістали 21. Яке невідоме число?
21: 3 = 7
Число 8 помножили на невідоме число і отримали в результаті число 56. Знайти невідоме число.
56: 8 = 7
2) знаходження діленого:
Невідоме число поділили на 5 і отримали 4. Знайти невідоме число.
4 · 5 = 20
3) знаходження дільника:
Число 27 зменшили в декілька разів і отримали 3. У скільки разів зменшили дане число?
27: 3 = 9 (р.)
