Ідея нескінченності натурального ряду чисел освоювалось дуже повільно через відсутність протягом тривалого історичного періоду зручної системи числення. Перші системи числення були дуже недосконалими: для зображення кожного числа використовували окремий знак – ієрогліф. Пізніше ієрогліфи стали використовувати лише для позначення так званих вузлових чисел, решту чисел зображали за допомогою їх за принципом додавання або віднімання.
Зміст стародавньої єгипетськоїієрогліфічної системи можна побачити у таблиці
| I | 
| 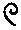
| 
| 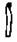
|
Стародавні єгиптяни лічили десятками. Але спеціальні знаки у них були лише для розрядів: одиниць, десятків, сотень і т. д. Числа від 1 до 10 записувались за допомогою паличок.
Наприклад, число 122 мало вид ς ∩∩I I.
У римський системі числення записували вузлові числа так: 1 - I, 5 – V, 10 – Х, 50 – L, 100 – C, 500 – D, 1000 – M. Решту чисел записували за принципом додавання або віднімання.
Наприклад, 256 – CCLVI, 399 – CCCXCIX.
Частково використовували і принцип множення: число 5 зображували символом руки, а 10 –як дві п’ятірки, тільки одна перевернута. Число 100 зображували буквою С, або (centum – сто), а 50 –L, як половину 100 (нижню половину).
Римською нумерацією користуємося і тепер. Ця система є непозиційною.
Непозиційними були також алфавітні системи: давньогрецька і старослов’янська. В цих системах перші 9 букв означали одиниці, наступні 9 – десятки, ще наступні – сотні.
У слов’янській нумерації було два способи лічби великих чисел: «мале словенське числення» і «велике словенське числення». У малому численні: 104 – тьма, 105 – легіон, 106 – леодр. У великому: тьма (@) – 106, легіон – 1012 – тьма тем, леодр – легіон легіонів – 1024, леодр леодрів – 1048 – ворон.
Перша позиційна система числення виникла понад 2000 років до н.е. в стародавньому Вавилоні. Це була шістдесяткова позиційна нумерація. Проте принцип позиційного значення цифр тут ще не використовувався скрізь. Для запису чисел використовували положення клину: ▼- 1 і 60, ◄ - 10. Інші числа зображувались за допомогою цих знаків і дій додавання.
Сучасна позиційна система числення була винайдена в Індії у V-VI ст. Через арабів вона поширилася в IX ст. в Середню Азію, а пізніше – і в Західну Європу. Великим досягненням індійської математики було введення нуля для позначення відсутності одиниць розряду в числі. Після цього десяткова система числення стала повністю оформленою. Запровадження десяткової системи числення на Русі було зупинено монгольським ігом. Тільки у XVIII ст. індійська система числення витіснила слов’янську нумерацію.
У сучасному житті використовують також інші системи числення. В астрономії з давніх-давен застосовується шістдесяткова система числення. Основою цієї системи є число 60. Так, 60сек = 1 мінута, або 60// = 1/, 60/ = 1° тощо.
Взагалі, основою числення може бути будь-яке натуральне число р ≥2. Для запису числа в такій системі числення використовується р символів: 0,1,..., р -1.
Означення: Записом цілого невід’ємного числа х у р -й системі числення називається його подання у вигляді х = аnpn + … + a1p + a0, де an , …, a1 , a0 набувають значення 0, 1,..., р -1, аn ≠ 0.
Числа 1, p, p2, …, pn називають розрядними одиницями 1-го, 2-го,..., (n +1)-го розрядів.




