План
1. Теоретико-множинний смисл різниці двох цілих невід’ємних чисел.
2. Означення різниці через суму. Зв’язок дії віднімання з дією додавання.
3. Умови існування різниці, її єдиність.
4. Правила віднімання.
5. Відношення «більше на», «менше на».
6. Прості задачі, які розв’язуються дією віднімання.
Теоретико-множинний смисл різниці двох цілих невід’ємних чисел
Розглянемо задачу: «В гаражі стояло 9 машин. 3 машини від’їхали. Скільки машин залишилось у гаражі?». Ця задача розв’язується виразом на віднімання: 9 − 3 = 6 (машин). Розв’язання цієї задачі пов’язано з виділенням з множини машин, які стояли у гаражі (число елементів її – 9) підмножини машин, які від’їхали (число елементів підмножини – 3) і знаходженням числа елементів у доповненні цієї підмножини, тобто множини машин, які залишились (число елементів доповнення – 6) до даної множини.
Означення. Різницею цілих невід'ємних чисел а і b називається число елементів в доповненні множини В до множини А, де n (А) = а, n (В) = b, B 
A, тобто а − b = n (A\B), де n (А) = а, n (В) = b, B A.
Різниця а – b не залежить від вибору множин, але таких, що n (А) = а, n (В) = b і B A.
Приклади:
1) A = { a, b, c, d }, B = { c, d }, тобто B A, n (A) = 4, n (B) = 2 
A\B = { a, b }, n (A\B) = 2 4 – 2 = 2.
2) A = {Δ, Δ, Δ, Ο}, B = {Ο}, тобто B A, n (A) = 5, n (B) = 1
A\B = { Δ, Δ, Δ }, n (A\B) = 4 5 – 1 = 4.
Дія, за допомогою якої знаходять різницю, називається відніманням. Компоненти дії віднімання – зменшуване (а) і від’ємник (b).
У початковому курсі математики ознайомлення з дією віднімання відбувається на основі практичних вправ, які пов’язані з вилученням підмножини елементів даної множини і утворенням нової множини, що є доповненням даної підмножини (без використання відповідної символіки та термінології). Основним засобом розкриття теоретико-множинного смислу віднімання є розв’язування простих текстових задач.
Означення різниці через суму. Зв’язок дії віднімання з дією додавання
Існує тісний зв’язок між додаванням і відніманням, тому правильність віднімання перевіряють додаванням.
Нехай дано цілі невід’ємні числа а і b такі, що а = n (A), b = n (B), B A і n (A\B) = а − b. За допомогою кругів Ейлера множини A, B і A\B зображуються так:
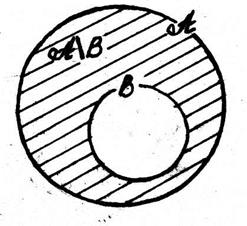
Так як A = B 
(A\B), то n (A) = n (B (A\B)). Так як B 
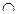(A\B) = 
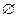, то n (A) = n (B (A\B)) = n (B) + n (A\B) = b + (а – b) = а різниця а – b – це таке число, яке в сумі з b дає число а. Тому маємо друге означення різниці: різницею цілих невід'ємних чисел а і b називається таке ціле невід’ємне число с, яке в сумі з числом в дає число а, тобто
а − b = c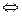 
а = b + с.
Дія віднімання є оберненою до дії додавання. Дії додавання і віднімання є діями І ступеня. Друге означення різниці встановлює зв’язок між цими діями і є основою правила знаходження невідомого доданка за відомою сумою і другим доданком.
