Добуток двох цілих невід’ємних чисел а і b не зміниться, якщо поміняти їх місцями, тобто 
.
Доведення.
Нехай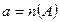 
, 
. За означенням добутку 
, 
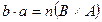. Між парами виду 
і парами виду 
існує взаємно однозначна відповідність, тобто 
. Отже, .
Асоціативний, або сполучний закон множення.
Добуток трьох цілих невід’ємних чисел не зміниться, якщо будь-які два послідовні множники замінити їхнім добутком, тобто 
.
Доведення.
Нехай , ,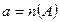 
.
За означенням добутку 
, 
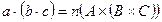. Між елементами 
і 
має місце взаємно однозначна відповідність, тобто 
. Отже, .
Дистрибутивний, або розподільний закон множення.
Для будь-яких цілих невід’ємних чисел 
виконується рівність 
, тобто, щоб помножити суму на число, досить помножити на це число кожен доданок і результати додати.
Доведення.
Використовуємо рівність для множин: 
, де 
Ø.
Нехай 
, 
, 
.
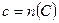За означенням добутку 
, 
. Отже, 
.
З рівності 
випливає дистрибутивний закон множення відносно різниці: 
.
Розподільні закони встановлюють зв'язок множення з додаванням і відніманням. Читати їх треба як зліва направо, так і справа наліво. На основі цих законів розкривають дужки і виносять спільні множники за дужки.
У початковій школі переставний закон використовується для складання таблиці множення, що дає змогу вдвоє зменшити кількість добутків одноцифрових чисел, які треба учням запам’ятати.
Обґрунтовують цей закон учням на конкретних доцільно підібраних задачах та за допомогою наочної ілюстрації.
Сполучний закон розглядається на конкретних задачах через розв’язання їх двома способами. Цей закон із комутативним законом множення широко використовують для раціональності обчислень. Наприклад:
, 
.
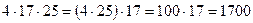Наслідок з переставного і сполучного законів множення: в добутку кількох множників їх можна переставляти і брати в дужки будь-яким чином. Наприклад: 
.
Розподільний закон множення обґрунтовується на конкретних задачах, які розв’язуються двома способами. Цей закон використовується для раціональності обчислень. Наприклад, 
Тема. Ділення на множині цілих невід’ємних чисел
План
1. Визначення поняття частки цілого невід’ємного числа і натурального через розбиття скінченної множини на еквівалентні підмножини, що попарно не перетинаються. Операція ділення на множині цілих невід’ємних чисел.
2. Зв’язок ділення з множенням.
3. Існування частки, її єдиність.
4. Правила ділення.
5. Неможливість ділення на нуль.
6. Ділення цілого невід’ємного числа на натуральне з остачею.
Визначення поняття частки цілого невід’ємного числа і натурального через розбиття скінченної множини на еквівалентні підмножини, що попарно не перетинаються. Операція ділення на множині цілих невід’ємних чисел
Розглянемо задачі, які розв’язують учні початкової школи вже в 2 класі.
1. 10 яблук розклали на дві тарілки порівну. По скільки яблук буде в кожній тарілці?
2. Скільки треба тарілок, щоб розкласти на них 10 яблук по 2 яблука на кожну тарілку?
В обох задачах розглядається множина, що складається з десяти елементів, вона розбивається на еквівалентні підмножини, що попарно не перетинаються.
У першій задачі відома кількість цих підмножин, їх дві. Потрібно знайти кількість елементів в кожній підмножині. Задача розв’язується дією ділення:
(яблук)
і такі задачі називають «задачами на ділення на рівні частини».
У другій задачі відома кількість елементів в кожній підмножині. Потрібно знайти кількість цих підмножин. Задача розв’язується дією ділення:
(тарілок)
і такі задачі називають «задачами на ділення на вміщення».
З теоретико-множинної точки зору обидві задачі приводять до подання скінченної множини А у вигляді об’єднання еквівалентних між собою (без спільних елементів) її підмножин. Перехід до чисельної характеристики такої задачі приводить до розгляду дії ділення на множині цілих невід’ємних чисел.
Означення. Нехай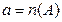 
і множина А розбита на еквівалентні множини без спільних елементів. Тоді, якщо b – число підмножин у розбитті множини А, то часткою чисел а і b називається число елементів кожної підмножини; якщо b – число елементів кожної підмножини в розбитті множини А, то часткою чисел а і b називається число підмножин у цьому розбитті.
Дія, за допомогою якої знаходиться частка 
, називається діленням. Числа при діленні називаються: а – ділене, b – дільник.
