Подільність цілих невід’ємних чисел

План

1. Відношення подільності на множині натуральних чисел, його властивості.

2. Теореми про подільність суми, різниці, добутку.

3. Ознаки подільності на 2 і 5, 4 і 25, 3 і 9, на складені числа.

4. Найбільший спільний дільник і найменше спільне кратне натуральних чисел, способи їх знаходження.

 

1. Відношення подільності на множині натуральних чисел, його властивості

Спостереження за виконанням арифметичних операцій над цілими невід’ємними числами привели ще стародавніх математиків до висновку: прямі операції (додавання, множення) над такими числами виконуються завжди, а обернені (віднімання і ділення) – ні. Тому важливо знати, при яких умовах виконуються обернені операції. Для віднімання достатньо впевнитися в тому, що зменшуване не менше за від’ємник. Для ділення такої простої ознаки немає. В результаті пошуків ще стародавніх математиків були знайдені ознаки подільності цілих невід’ємних чисел. Але спочатку введемо поняття відношення подільності на множині цілих невід’ємних чисел.

Означення. Говорять, що ціле невід’ємне число а ділиться на натуральне число b, якщо існує таке ціле невід’ємне число q, що а = bq.

Говорять «число а кратне числу b». Відношення подільності числа a на число b символічно позначають а 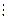b. Відношення подільності не означає операції, тому не можна писати а 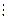b = q. Наприклад, число а = 24 ділиться на число b = 6, бо існує таке число q = 4, що 24 = 6∙4.

Чисел, кратних даному числу – нескінченна множина. Наприклад, усі парні числа кратні числу 2. Їх можна знайти за формулою х = 2∙ q, де q набуває значення 0, 1, 2, 3,....

Число 1 ділиться тільки само на себе; числа 2, 3, 5, 7,... діляться самі на себе і на одиницю; числа 4, 6, 8, 9,... мають більше двох дільників. Ці спостереження привели математиків до введення понять простого і складеного числа.

Означення. Натуральне число, яке має лише два дільники, називається простим.

Отже, числа 2, 3, 5, 7 – прості числа.

Означення.Натуральне число, яке має більше двох дільників, називається складеним.

Такими числами є 4, 6, 8, 9. Так число 6 має дільники 1, 2, 3, 6. Оскільки число 1 має тільки один дільник, то його не відносять ні до простих, ні до складених.

 

 

Властивості відношення подільності:

Рефлексивність.

Оскільки для будь-якого невід’ємного числа а виконується рівність а = а ∙ 1, тобто будь-яке ціле невід’ємне число ділиться само на себе (а 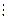а), то відношення подільності на цій множині чисел – рефлексивне.

Антисиметричність.

Для невід’ємних цілих чисел а і b, для яких виконуються відношення а 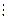b і b 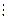а, маємо, що а = b, тобто відношення подільності невід’ємних чисел антисиметричне.

Транзитивність.

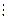(а b) q (a = b∙q) (b a) q₁ (b = cq₁). Тому а = b q = cqq₁ = cq₂.

Отже, а 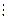с.

 

Отже, відношення подільності на множині N₀ цілих невід’ємних чисел має властивості рефлективності, антисиметричності і транзитивності, тобто є відношенням нестрогого порядку, причому часткового порядку, бо не кожна пара цілих невід’ємних чисел знаходиться у відношенні подільності. Наприклад, і .