Розглянемо дві задачі.
1) «На тарілці лежать 3 груші і 5 яблук. Скільки всього фруктів на тарілці?»
Задача розв’язується виразом на додавання 3 + 5 = 8, бо мова йде про об’єднання двох множин: множини груш (число елементів – 3) та множини яблук (число елементів – 5). Ці множини не перетинаються. Щоб знайти, скільки всього фруктів на тарілці, треба об'єднати множини груш та яблук і полічити, скільки всього елементів у цьому об’єднанні. Число елементів об’єднання даних множин дорівнює 8; тобто 8 фруктів на тарілці.
2) «Знайти кількість елементів в об’єднанні множин A = { k, l, m, n } та B = { n, o, p }».
Розв’язання. Кількість елементів множини A: n (A) = 4, а кількість елементів множини B: n (B) = 3. За означенням A  B = { k, l, m, n, o, p }
B = { k, l, m, n, o, p }  n (A
n (A  B) = 6. Але n (A
B) = 6. Але n (A  B) ≠ 4 + 3. Чому? Тому, що А
B) ≠ 4 + 3. Чому? Тому, що А 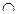 В = { n } і, отже,
В = { n } і, отже,
n (A) + n (B) ≠ n (A  B).
B).
Звідси, суму цілих невід’ємних чисел визначають через об’єднання двох множин, що не перетинаються.
Означення. Сумою двох цілих невід’ємних чисел а і b називається число елементів в об’єднанні множин А і В, які не перетинаються і таких, що n (А) = а, п (В) = b, тобто а + b = п (А  В), де а = п (А), b = п (В), А
В), де а = п (А), b = п (В), А 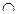 В =
В = 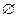 .
.
Сума  не залежить від вибору двох множин, що не перетинаються, але таких, що n (A) = a і n (B) = b.
не залежить від вибору двох множин, що не перетинаються, але таких, що n (A) = a і n (B) = b.
Приклади:
1) A = { a, b }, B = { c, d }  A
A  B = { a, b, c, d } і А
B = { a, b, c, d } і А 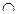 В =
В = 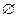 , отже, n (A
, отже, n (A  B) = n (A) + n (B) = 2 + 2 = 4, де n (A) = 2, n (B) = 2.
B) = n (A) + n (B) = 2 + 2 = 4, де n (A) = 2, n (B) = 2.
2) A = {Δ, Δ}, B = {Ο, Ο}  A
A  B = {Δ, Δ, Ο, Ο} і А
B = {Δ, Δ, Ο, Ο} і А 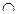 В =
В = 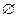 , отже, n (A
, отже, n (A  B) = n (A) + n (B) = 2 + 2 = 4, де n (A) = 2, n (B) = 2.
B) = n (A) + n (B) = 2 + 2 = 4, де n (A) = 2, n (B) = 2.
Дія, за допомогою якої знаходять суму, називається додаванням. Числа, які додаються, називаються доданками.
У початковому курсі математики додавання цілих невід’ємних чисел вводиться на основі виконання практичних вправ, пов’язаних з об’єднанням двох множин предметів (без використання відповідної символіки та термінології). Основним засобом розкриття теоретико-множинного смислу додавання є розв’язування простих текстових задач.
Існування суми, її єдиність
Теорема: « Сума цілих невід’ємних чисел завжди існує і вона єдина».
(Доведення теореми випливає з теореми про існування і єдиність операції об'єднання множин).
Іншими словами, які б не було взято два цілих невід’ємних числа а і b, завжди можна знайти їх суму – ціле невід’ємне число с, яке і буде єдиним для заданих чисел а і b.
Сума декількох доданків
Нехай сума двох доданків визначена і визначена сума п доданків. Тоді сума, що складається з n +1 доданка, тобто сума а1 + а2 +... + ап + ап+1 дорівнює (а1 + а2 +... + ап) + ап+1, тому
а1 + а2 +... + ап + ап+1 = (а1 + а2 +... + ап) + ап+1 .
Приклад:  .
.
Закони додавання
· Комутативний (переставний) закон: «Для будь-яких цілих невід’ємних чисел а і b виконується рівність: а + b = b + а.»
Доведення. Нехай а – кількість елементів множини A, b – кількість елементів множини B, тобто n (A) = а, n (B) = b і А  В =
В =  . Тоді за означенням суми цілих невід’ємних чисел а + b = n (A
. Тоді за означенням суми цілих невід’ємних чисел а + b = n (A  B). А так як A
B). А так як A  B = B
B = B  A (за комутативним законом об’єднання множин), то n (A
A (за комутативним законом об’єднання множин), то n (A  B) = n (B
B) = n (B  A)
A)  за означенням суми n (B
за означенням суми n (B  A) = b + а
A) = b + а  а + b = b + а для будь-яких цілих невід’ємних чисел.
а + b = b + а для будь-яких цілих невід’ємних чисел.
· Асоціативний (сполучний) закон: «Для будь-яких цілих невід’ємних чисел а, b, с виконується рівність: (a + b) + с = а + (b + с)».
Доведення. Нехай а – кількість елементів множини A, b – кількість елементів множини B, с – кількість елементів множини С, тобто n (A) = а, n (B) = в, n (С) = с, А 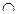 В =
В = 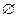 , B
, B 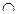 С =
С = 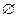 . Тоді за означенням суми двох цілих невід’ємних чисел (а + b) + с = n (A
. Тоді за означенням суми двох цілих невід’ємних чисел (а + b) + с = n (A  B) + n (C) = n ((A
B) + n (C) = n ((A  B)
B)  C). Так як за асоціативним законом об’єднання множин (A
C). Так як за асоціативним законом об’єднання множин (A  B)
B)  С = =A
С = =A  (B
(B  C), то n ((A
C), то n ((A  B)
B)  С) = n (A
С) = n (A  (B
(B  C))
C))  за означенням суми двох чисел n (A
за означенням суми двох чисел n (A  (B
(B  C)) = n (A) + n (B
C)) = n (A) + n (B  C) = а + (b + с)
C) = а + (b + с)  (а + b) + + с = а + (b + с).
(а + b) + + с = а + (b + с).
· Властивість монотонності додавання: «Для будь-яких цілих невід’ємних чисел а, b, m таких, що а = b виконується рівність:  ».
».
Наслідки із комутативного та асоціативного законів додавання:
· Додавання числа до суми і суми до числа.
1) (а + b) + с = (а + с) + b = а + (b + с);
2) а + (b + с) = (а + b) + с =:(а + с) + b.
Додати число до суми або суму до числа можна двома способами: обчислити суму і до результату додати дане число або додати це число до одного з доданків, а до результату додати другий доданок.
· Додавання суми до суми.
(а + b) + (с + d) = (а + с) + (b + d) = (а + d) + (b + с).
Для того щоб додати суму до суми, можна до одного з доданків першої суми додати один із доданків другої, а до другого доданку першої суми – інший доданок другої суми і одержані результати додати.
Ці правила легко поширити на будь-яку кількість доданків і об’єднати їх одним правилом: якщо при додаванні маємо дужки, то їх можна опустити і об’єднати між собою доданки в будь-якій послідовності так, щоб обчислення виконувати найзручнішим способом.
Із законами дії додавання учні початкових класів знайомляться поступово: спочатку вивчають переставну властивість додавання (1 клас), яка використовується при складанні таблиць додавання одноцифрових чисел, а далі для розкриття прийомів додавання та раціоналізації обчислень. В 4 класі при узагальненні і систематизації знань про дію додавання закони – переставний і сполучний формулюються та записуються у буквеному вигляді.






