В установленные сроки каждый студент должен выполнить контрольную работу.
Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию у преподавателя.
Контрольная работа должна быть сделана в отдельной тетради, на обложке которой студенту следует разборчиво написать свою фамилию и инициалы, шифр, название дисциплины, дату отправки в колледж.
Каждый студент выбирает тот вариант контрольной работы, который соответствует порядковому номеру в журнале.
Решение задач необходимо приводить в той же последовательности, в которой представлены контрольные задания. При этом условие задачи должно быть полностью переписано перед её решением.
На последней странице текста поставьте дату выполнения и подпись. Оставьте чистую страницу для рецензий преподавателя.
После проверки контрольная работа возвращается студенту, который должен рассмотреть замечания и, при необходимости выполнить по этим замечания доработку контрольной работы.
Проверенная преподавателем контрольная работа хранится у студента и на экзамене предъявляется преподавателю.
Критерием оценки контрольной работы по дисциплине является уровень умений обучающимся применять полученные теоретические знания для решения практических задач.
Критерии оценки знаний и умений в контрольной работе:
- задания выполнены в полном объеме – оценка «зачтено»;
- задания выполнены не полностью – оценка «не зачтено».
ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАНИЕ 1.
Выполнить операции над матрицами
| 1. | 1.Найти  , если , если  , ,  2.Найти
2.Найти  , если
a) , если
a)  , ,  b)
b)  , , 
|
| 2. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a) 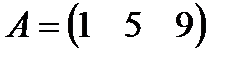 , ,  b)
b)  , , 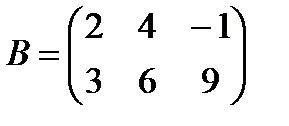
|
| 3. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 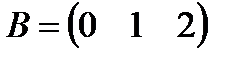
|
| 4. | 1. Найти  , если , если  , , 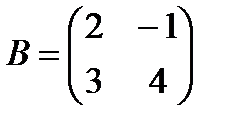 2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 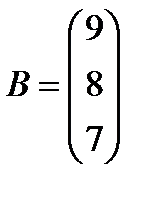
|
| 5. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , , 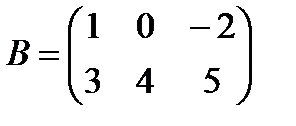 b)
b)  , , 
|
| 6. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 
|
| 7. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 
|
| 8. | 1. Найти  , если , если  , , 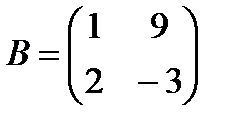 2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b) 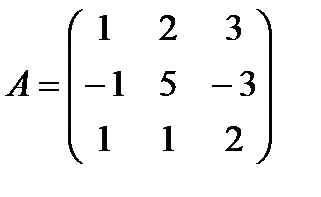 , , 
|
| 9. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 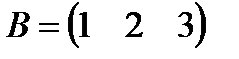
|
| 10. | 1. Найти  , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , , 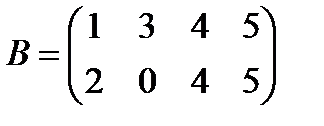 b)
b)  , , 
|
| 11. | 1. Найти 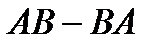 , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 
|
| 12. | 1. Найти  , если , если  , , 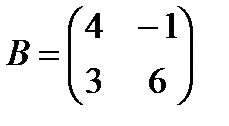 2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 
|
| 13. | 1.Найти 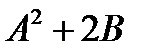 , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b) 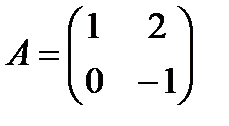 , , 
|
| 14. | 1. Найти 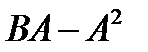 , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b)  , , 
|
| 15. | 1. Найти 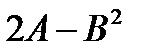 , если , если  , ,  2. Найти
2. Найти  , если
a) , если
a)  , ,  b)
b) 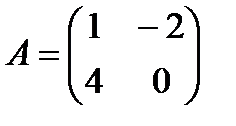 , , 
|
ЗАДАНИЕ 2
Решить систему линейных уравнений: а) по правилу Крамера; б) матричным методом; в) методом Гаусса:
| 1. | 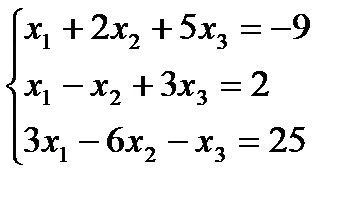
| 2. | 
|
| 3. | 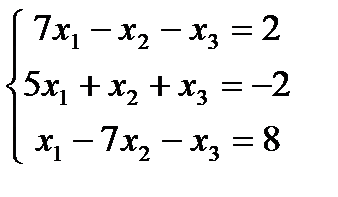
| 4. | 
|
| 5. | 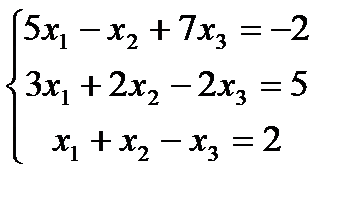
| 6. | 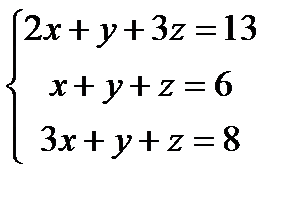
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 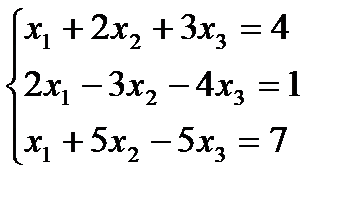
| 14. | 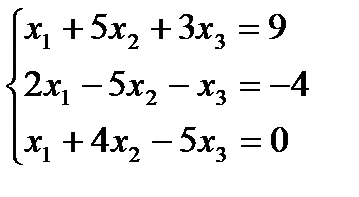
|
| 15. | 
|
ЗАДАНИЕ 3
Найти пределы функций, не пользуясь правилом Лопиталя
| 1. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 2. | a) 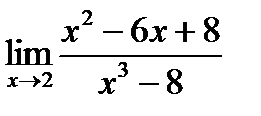
| b) 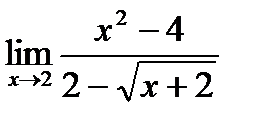
| c) 
| |||||||||||||||||||||||||
d) 
| e) 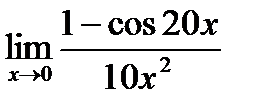
| f) 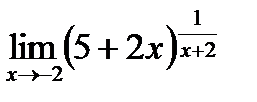
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 3. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 4. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 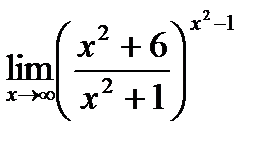
| ||||||||||||||||||||||||||||
| 5. | a) 
| b) 
| c) 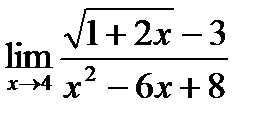
| |||||||||||||||||||||||||
d) 
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 6. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 
| f) 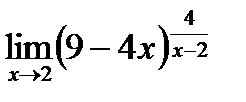
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 7. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 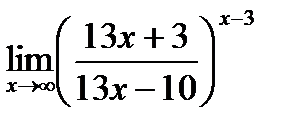
| ||||||||||||||||||||||||||||
| 8. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 
| f) 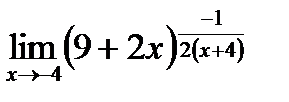
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 9. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 
| e) 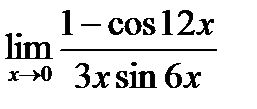
| f) 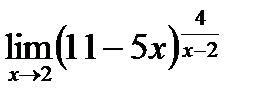
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 10. | a) 
| b) 
| c) 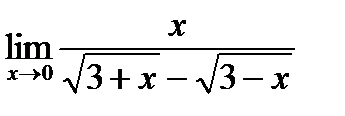
| |||||||||||||||||||||||||
d) 
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 11. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 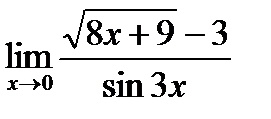
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 12. | a) 
| b) 
| c) 
| |||||||||||||||||||||||||
d) 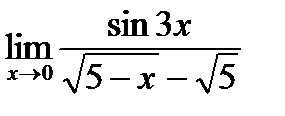
| e) 
| f) 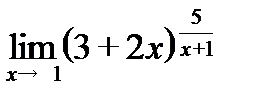
| ||||||||||||||||||||||||||
g) 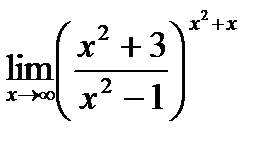
| ||||||||||||||||||||||||||||
| 13. | a) 
| b)
| c) 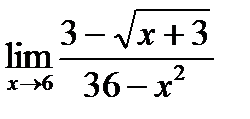
| |||||||||||||||||||||||||
d) 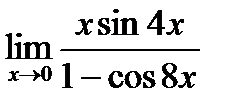
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 14. | a) 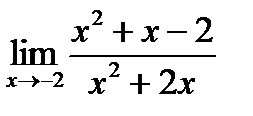
| b) 
| c) 
| |||||||||||||||||||||||||
d) 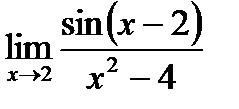
| e) 
| f) 
| ||||||||||||||||||||||||||
g) 
| ||||||||||||||||||||||||||||
| 15. | a) 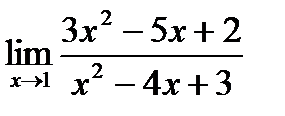
| b) 
| c) 
| |||||||||||||||||||||||||
d) 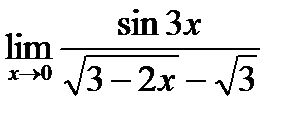
| e) 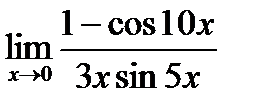
| f) 
| ||||||||||||||||||||||||||
g) 
|
ЗАДАНИЕ 4
Функция  задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют, и построить график функции.
задана различными аналитическими выражениями в различных областях изменения независимой переменной. Найти точки разрыва функции, если они существуют, и построить график функции.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10.
|
11.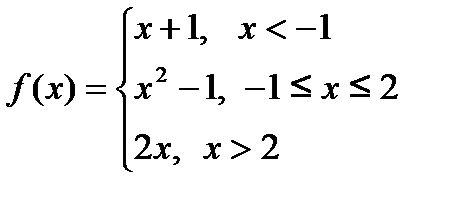
| 12.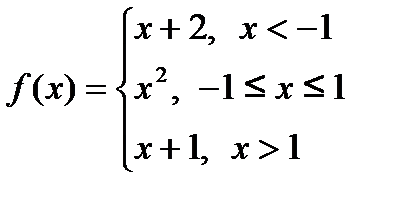
|
13.
| 14.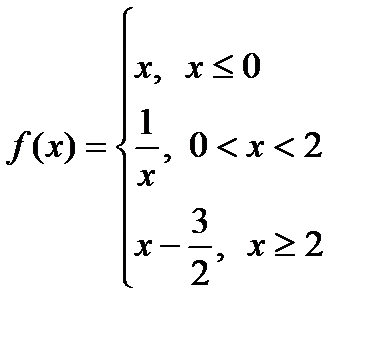
|
15.
|
ЗАДАНИЕ 5
Найти производные следующих функций
| 1. | a) 
| b) 
|
c) 
| d) 
| |
e) 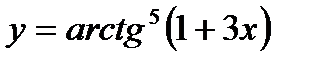
| ||
| 2. | a) 
| b) 
|
c) 
| d) 
| |
e) 
| ||
| 3. | a) 
| b) 
|
c) 
| d) 
| |
e) 
| ||
| 4. | a) 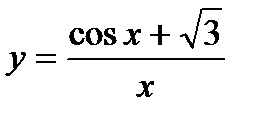
| b) 
|
c) 
| d) 
| |
e) 
| ||
| 5. | a) 
| b) 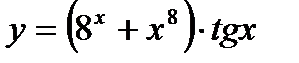
|
c) 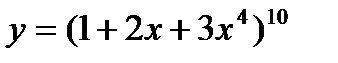
| d) 
| |
e) 
| ||
| 6. | a) 
| b) 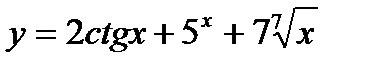
|
c) 
| d) 
| |
e) 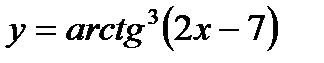
| ||
| 7. | a) 
| b) 
|
c) 
| d) 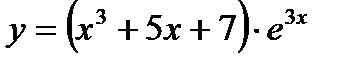
| |
e) 
| ||
| 8. | a) 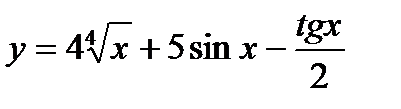
| b) 
|
c) 
| d) 
| |
e) 
| ||
| 9. | a) 
| b) 
|
c) 
| d) 
| |
e) 
| ||
a) 
| b) 
| |
c) 
| d) 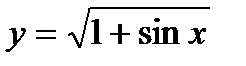
| |
e) 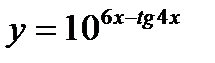
| ||
| 11. | a) 
| b) 
|
c) 
| d) 
| |
e) 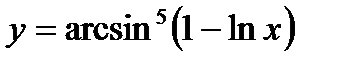
| ||
| 12. | a) 
| b) 
|
c) 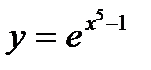
| d) 
| |
e) 
| ||
| 13. | a) 
| b) 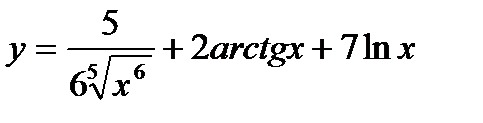
|
c) 
| d) 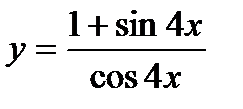
| |
e) 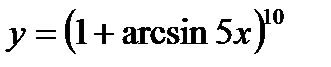
| ||
| 14. | a) 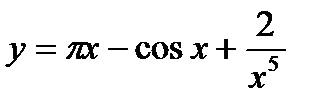
| b) 
|
c) 
| d) 
| |
e) 
| ||
| 15. | a) 
| b) 
|
c) 
| d) 
| |
e) 
|
ЗАДАНИЕ 6
Найти пределы функций с помощью правила Лопиталя
| 1. | a) 
| b) 
| c) 
|
| 2. | a) 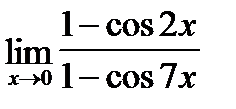
| b) 
| c) 
|
| 3. | a) 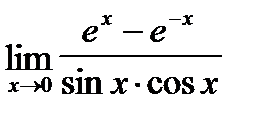
| b) 
| c) 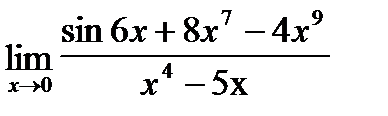
|
| 4. | a) 
| b) 
| c) 
|
| 5. | a) 
| b) 
| c) 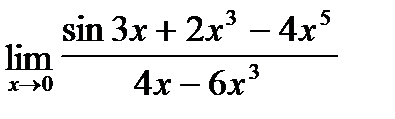
|
| 6. | a) 
| b) 
| c) 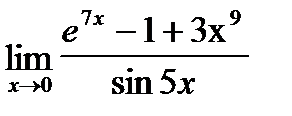
|
| 7. | a) 
| b) 
| c) 
|
| 8. | a) 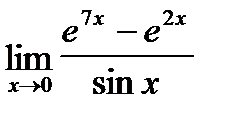
| b) 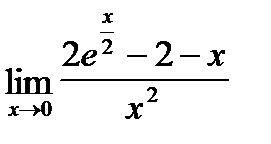
| c) 
|
| 9. | a) 
| b) 
| c) 
|
| 10. | a) 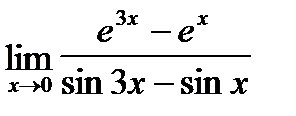
| b) 
| c) 
|
| 11. | a) 
| b) 
| c) 
|
| 12. | a) 
| b) 
| c) 
|
| 13. | a) 
| b) 
| c) 
|
| 14. | a) 
| b) 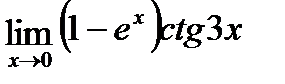
| c) 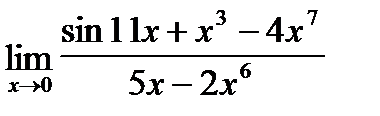
|
| 15. | a) 
| b) 
| c) 
|
ЗАДАНИЕ 7
Провести полное исследование и построить график функции
| 1. | 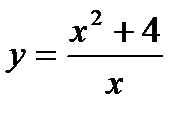
| 2. | 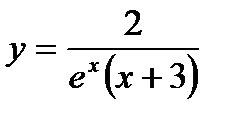
| 3. | 
|
| 4. | 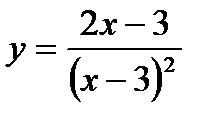
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
| 9. | 
|
| 10. | 
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 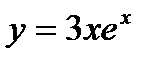
| 15. | 
|
ЗАДАНИЕ 8
Найти следующие интегралы методом подстановки
| 1. | a) | 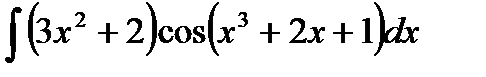
| b) | 
|
| c) | 
| |||
| 2. | a) | 
| b) | 
|
| c) | 
| |||
| 3. | a) | 
| b) | 
|
| c) | 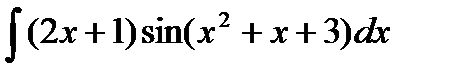
| |||
| 4. | a) | 
| b) | 
|
| c) | 
| |||
| 5. | a) | 
| b) | 
|
| c) | 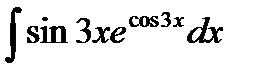
| |||
| 6. | a) | 
| b) | 
|
| c) | 
| |||
| 7. | a) | 
| b) | 
|
| c) | 
| |||
| 8. | a) | 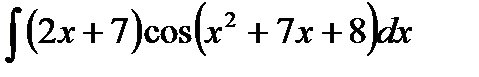
| b) | 
|
| c) | 
| |||
| 9. | a) | 
| b) | 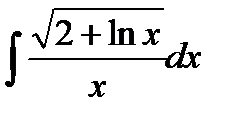
|
| c) | 
| |||
| 10. | a) | 
| b) | 
|
| c) | 
| |||
| 11. | a) | 
| b) | 
|
| c) | 
| |||
| 12. | a) | 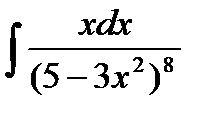
| b) | 
|
| c) | 
| |||
| 13. | a) | 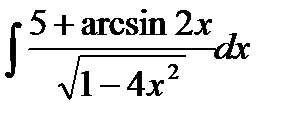
| b) | 
|
| c) | 
| |||
| 14. | a) | 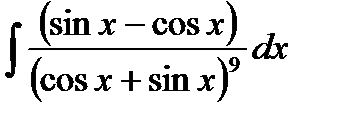
| b) | 
|
| c) | 
| |||
| 15. | a) | 
| b) | 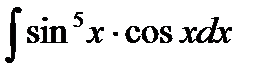
|
| c) | 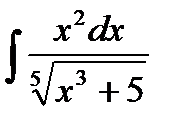
|
ЗАДАНИЕ 9
Найти следующие интегралы методом интегрирования по частям
| 1. | a) | 
| b) | 
|
| 2. | a) | 
| b) | 
|
| 3. | a) | 
| b) | 
|
| 4. | a) | 
| b) | 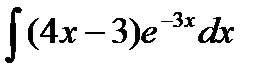
|
| 5. | a) | 
| b) | 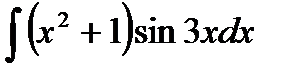
|
| 6. | a) | 
| b) | 
|
| 7. | a) | 
| b) | 
|
| 8. | a) | 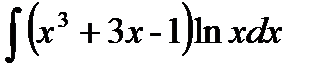
| b) | 
|
| 9. | a) | 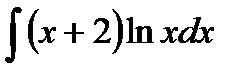
| b) | 
|
| 10. | a) | 
| b) | 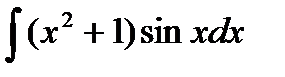
|
| 11. | a) | 
| b) | 
|
| 12. | a) | 
| b) | 
|
| 13. | a) | 
| b) | 
|
| 14. | a) | 
| b) | 
|
| 15. | a) | 
| b) | 
|
ЗАДАНИЕ 10
Найти площадь фигуры, ограниченной заданными линиями. Сделать рисунок.
| 1. | 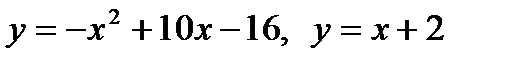
| 9. | 
|
| 2. | |||
|
|
|
|
|
|
Дата добавления: 2016-11-20; Мы поможем в написании ваших работ!; просмотров: 506 | Нарушение авторских прав
Лучшие изречения:






